0 引言

震级是表示地震本身大小的量，是地震的基本参数之一。无论是从科学研究的角度，还是从社会需求的角度，衡量地震的大小都是一件意义重大的基础性工作。然而，对于大地震而言，常规量取体波和面波振幅的方法存在震级饱和的缺点（刘瑞丰等，2018），只有矩震级才能较准确地量度地震大小，在国际地震学界，一直推荐矩震级作为衡量地震大小的首选震级。刘瑞丰等（1999）在反演矩张量时，采用线性反演方法，从而使地震矩张量反演由研究工作向常规处理工作迈出了重要一步。在日常工作中，一般利用波形数据反演矩张量，从而确定矩震级大小，若快速确定震级大小，必须使用近场波形资料。遗憾的是，用近场波形记录反演矩震级比较困难。其主要原因是，近震波形记录不能完全反映整个地震的破裂过程，且受到震源区小尺度非均匀介质的强烈影响，这就使得在反演震源参数时，应用高频近场波形记录比低频远震记录要困难得多。对于近场记录而言，矩张量反演一般只能用来处理中小地震，如：吴忠良等（1994）的研究结果表明，采用简单的均匀弹性半空间模型，用近震源宽频带记录进行矩张量反演，对于M_L＜4的小震，可以较好地给出震源机制和地震矩。

如何快速测定地震大小是地震学家需要解决的一个重大问题。地震发生后，震源发出的P波和S波携带各种地震信息被记录到，且振幅较小的P波先于S波到达，为此，许多学者利用宽频带P波初动记录来快速估算矩震级M_WP（Tsuboi et al，1995；Allen et al，2003）。利用该方法可以较好地得到中等强度地震的矩震级，但对于强度较大的地震，震级往往被低估（孙丽等，2016；陈晓佳等，2018）。Wu等（2004）对近场加速度记录进行积分，计算地震事件持续时间内加速度记录绝对振幅之和，以此作为事件总的有效振动，从而估算矩震级。实际工作中，快速确定震级需要在快速性和准确性二者间折中。要得到较准确的震级，就需要较长的时间和丰富的波形资料；相反，在较短时间内确定震级，震级误差往往较大。就地震速报需要而言，Wu等（2004）提出的地震参数M_ew测定方法，可以近实时地确定可靠的M_ew，且容易实现近实时自动处理，并能解决复杂的多次破裂地震导致的震级不稳定问题，比较适合速报工作需求。因此，Wu等（2004）提出的M_ew测定方法值得好好研究和应用。

本研究将参考Wu等（2004）提出的方法，选取地震台站密度高、地震多发的川滇地区作为研究区域，使用中强地震近场（震中距小于2°）台站速度波形记录，研究地震事件持续时间内加速度记录的绝对振幅之和与矩震级、震中距之间的关系，并拟合得到三者之间的关系式。将该关系式应用到实际震级测定工作中，可为近实时区域测震台网速报提供快速可靠的震级，提升中国地震台网对全球地震活动的测定能力。

1 M_ew测定方法

据Wu等（2004）的研究，在计算整个近场加速度记录波形的有效震动时，定义了振幅绝对值的积分值$\sqrt {{E_{\rm{S}}}} $，公式如下

$ \sqrt {{E_{\rm{S}}}} = \int_{{T_{\rm{P}}}}^{{T_{\rm{e}}}} {\sqrt {{V^2} + {N^2} + {E^2}} {\rm{d}}t} $

(1)

式中：V、N和E分别为垂直、南北和东西分向加速度记录（单位cm·s^-2）；$\sqrt {{E_{\rm{S}}}} $为速度量纲，其大小与地震波能量成正比；T_P为P波起始时间，单位s；T_e为强震动持续记录的结束时间，可以定义为当加速度振幅减小至最大振幅的20%后持续5 s的时间点，单位s。

地震波振幅A随震源距的增加而衰减，可以表示为

$ A \sim {e^{ - \gamma R}}/{R^n} $

(2)

式中，R为震源距，n为几何扩散系数，γ与滞弹性衰减系数Q相关。在震级计算过程中，震级与logA成正比，logA可表示为nlogR - (γ/ln10)R + C_S，C_S为常数。

在本研究中，$\sqrt {{E_{\rm{S}}}} $表示加速度记录振幅绝对值的积分值，则可定义以下线性回归模型

$ \log \sqrt {{E_{\rm{S}}}} {\rm{ = }}A + B{M_{\rm{W}}} + CR + D\log R + {S_i} $

(3)

式中，S_i为第i个场地相关因子，A、B、C、D为待定系数。

全球主要大地震发生后，美国哈佛大学全球矩心矩张量研究组（GCMT）在短时间内发布地震矩震级M_W。可以通过大量近场波形数据计算$\sqrt {{E_{\rm{S}}}} $值，并收集对应的GCMT矩震级M_W，利用式（3），计算线性回归待定系数值，则矩震级M_W可表示为

$ {M_{\rm{W}}}{\rm{ = }}\frac{{\log \sqrt {{E_{\rm{S}}}} }}{B} - \frac{A}{B} - \frac{{CR}}{B} - \frac{{D\log R}}{B} - \frac{{{S_i}}}{B} $

(4)

用一个新的地震参数M_ew与矩震级M_W对接，则式（4）变为

$ {M_{{\rm{eW}}}}{\rm{ = }}\frac{{\log \sqrt {{E_{\rm{S}}}} }}{B} - \frac{A}{B} - \frac{{CR}}{B} - \frac{{D\log R}}{B} - \frac{{{S_i}}}{B} $

(5)

式中，A、B、C、D为待定常数，R为震源距，E_S为(V² + N² + E²)(T_e² -T_P²)，S_i为第i个场地相关因子。

综上，大地震发生后，利用近场台站记录的大量波形，地震速报机构即可将M_ew测定公式应用于实际地震速报工作，快速估算地震参数M_ew。

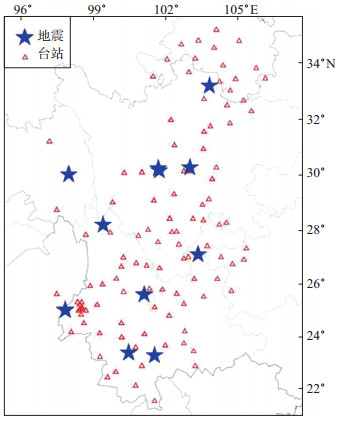
2 资料选取

收集整理2009年1月1日至2018年12月31日在川滇地区（97°—108°E，21°—34°N）发生的M_W≥5.7、深度≤50 km的12次地震事件波形（表 1），其中M_W震级来自哈佛大学全球CMT地震目录，震级最大地震为2013年4月20日四川芦山M_W 6.6地震。选取震中距2°以内的90个台站三分量宽频速度记录，各地震事件记录台站均围绕地震有较好的分布（图 1），将所得记录去除均值、倾斜值及仪器响应，进行微分处理，将速度记录转化为加速度记录，累计得到145条可使用的台站记录。

3 线性回归分析及M_ew测定实例 3.1 回归分析

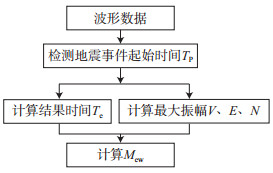
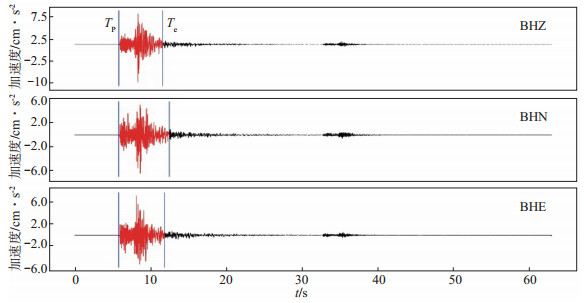
基于中国数字地震台网记录的速度波形资料，采用Wu等（2004）提出的M_ew地震参数测定方法，自动检测事件起始时间T_P和计算结束时间T_e，自动计算三分量最大振幅值，实现近实时自动测定川滇地区较大地震事件震级，测定流程见图 2。在检测地震事件时，采用长短时平均（STA/LTA）方法（Trnkoczy，2002；郭铁龙等，2017），自动识别地震P波初动（图 3）。

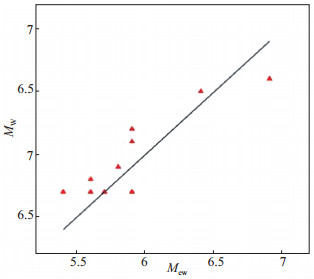
应用中国地震数字台网对川滇地区12次地震的同期速度记录，由公式（5）计算得到对应的M_ew（表 1），并与全球矩心矩张量计算所得M_W（GCMT结果）进行比较，结果见图 4。由表 1、图 4可知，M_ew与M_W具有较好的一致性，无明显系统偏差，二者平均标准差为0.19，震级偏差范围为-0.2—0.3。M_ew与M_W虽略有差别，但也说明，利用加速度绝对值积分快速估算矩震级并用于地震速报是可行的。

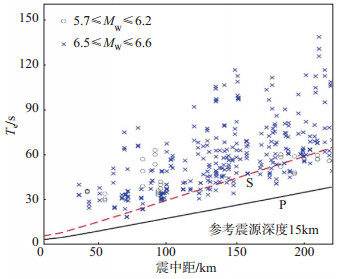
将12次地震的145条强震动记录持续时间进行统计，得到各条持续记录的结束时间T_e，假设地震震源深度为15 km，采用IASP91一维速度模型，计算P波和S波的理论走时，结果见图 5中的黑线和红色虚线。由图 5可见，强震动记录多在P波到达后2 min内结束。也就是说，使用震中距2°以内的台站记录，约2 min即可估算出地震大小。对于地震预警工作而言，时间有点长，但该时间满足当前速报工作需求。

采用非线性曲线方法，将145条强震动记录进行拟合，得到川滇地区$\log \sqrt {{E_{\rm{S}}}} $与M_W的线性回归经验关系式

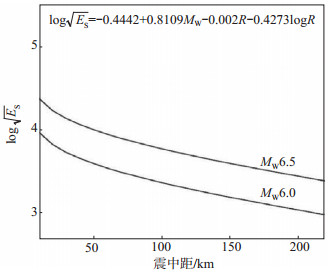
$ \log \sqrt {{E_{\rm{S}}}} = - 0.4442 + 0.8109{M_{\rm{W}}} - 0.002R - 0.4273\log R $

(6)

由式（6）可知，logE_S与M_W成正相关。设M_W = 6.0、6.5，由式（6）计算震中距2°范围内的$\log \sqrt {{E_{\rm{S}}}} $，拟合得到2条经验回归曲线，见图 6。

据2条经验曲线，若已知近场波形数据，便可准实时确定川滇地区某些地震的M_ew，具体计算公式可以表示为

$ {M_{{\rm{eW}}}}{\rm{ = }}0.6166{E_{\rm{S}}} + 0.002R + 0.2569\log R + 0.5478 $

(7)

3.2 M_ew测定实例

基于本研究给出的M_ew震级测定公式，利用中国地震台网实时波形数据，实现了对川滇地区中强地震强度的准实时测定。2019年6月17日四川长宁发生M 6.0（M_W 5.8）地震邹立晔等（2019），使用四川、云南、贵州和重庆区域测震台网共23个地震台站的波形数据，根据公式（7），计算该地震震级，得到地震参数M_ew为5.7，与M_W相差0.1，在误差范围内，表明准实时测定地震参数M_ew的方法是可行的。

4 结论与讨论

测定川滇地区12次M_W 5.7以上地震事件的矩震级M_ew，得出适合川滇地区中强地震矩震级估算公式。将12次地震的M_ew与全球矩心矩张量的M_W进行比较，可见二者具有较好的一致性。M_ew与M_W的平均标准差为0.19，震级偏差范围为-0.2—0.3，无显著震级偏差。

准实时自动测定与发布地震参数是当今全球各地震台网的主流业务，快速稳定的震级测定方法是必然选择。相比传统的M_L、M_S等根据振幅测定震级的标度，M_ew有一个显著优点，即不会出现震级饱和现象；对于大地震而言，相比M_WP，M_ew不会出现震级偏小的现象；此外，相比M_W，M_ew在计算方法上更加简单易行，也就更加具有时效性。研究过程中，我们尝试应用速度记录来自动测定地震大小，并取得较好的研究结果，为高密度台站的速度记录应用提供了参考。需要注意的是，研究中的加速度记录由速度记录微分转化而来，速度记录中的低频长周期成分可能导致误差累积，从而影响测定结果的精度。

随着中国地震局“国家地震烈度速报与预警工程”项目的开启，我国地震预警工程建设进入白热化阶段，各省区域地震监测台网的台站分布将更加密集，大量的宽频带、大动态、高分辨率、高智能的地震仪器布设，将给近场地震观测带来新的发展和变革。在今后的工作中，将应用更多的速度记录和加速度记录开展更加精细的矩震级测定工作，提高大地震震源测定的实时性和准确性，为大地震应急救援和海啸预警提供更可靠的技术支撑。