一般,将接收的远震体波去除震源、传播路径及仪器影响后得到的反映地震台站下方地壳和上地幔结构的时间序列称为接收函数(Langston,1979;Owens et al,1984)。自1984年Owens将该方法引入宽频带地震计以来,接收函数已成为研究地震台站下方地壳结构的常规手段,各种利用接收函数获取台站下方地壳介质结构参数的方法层出不穷(Zhu et al,2000;Bianchi et al,2010;Liu et al,2012)。随着观测资料长时间的积累,研究人员开始利用不同方位角的接收函数提取台站下方地壳介质的各向异性和莫霍界面的倾斜等信息。为了方便地提取地壳结构变化的信息,近来主成分分析方法(Principal Component Analysis,PCA)被引入接收函数分析(张建勇等,2019)。
PCA作为一种多元统计技术,是基于统计特征的多维正交线性变换,常用于提取信号特征(赵秀红,2016)和对数据进行降维。它由Pearson于1901年首先提出,随后由Hotelling、Jackson等学者进行了发展。目前该方法广泛应用于化学、模式识别、图像处理等领域。PCA方法是面向模式分类中用于特征提取的(陈佩,2014)的典型工具,可以在不减少原始数据所包含信息的前提下,将原始数据集转化为低维的有效特征成分来表示,使其在统计均方意义下达到方差最优的目的。
张建勇等(2019)基于理论模型,使用PCA方法提取接收函数特征成分,论证地壳结构的可行性和适用性,结果表明,径向接收函数的第一主成分包含数据主体信息,反映台站下方一维平均地壳结构特征;而其第二主成分、第三主成分以及切向接收函数第一主成分则反映台站下方地壳结构的变化特征。主成分分析方法可以有效地分离台站下方的界面倾斜和各向异性等横向不均匀性,基于第二、三主成分的震相变化花样还可以反演横向不均匀性的参数特征。张建勇等(2019)未对主成分的贡献率进行详细论述,也未对倾斜界面和各向异性同时存在下的结构参数反演进行深入分析。本文尝试基于理论模型,使用PCA方法,研究在倾斜界面和各向异性共存情况下的接收函数,分析主成分贡献率与地壳横向不均匀性的关系,并进一步验证该方法分离界面倾斜和各向异性的效果,并以江西省余干地震台为例,探讨台站下方地壳介质结构变化特征。
1 方法及理论测试 1.1 主成分的贡献率和累计贡献率为了表示主成分对原始数据集信息的反映,引入主成分的贡献率和累计贡献率。它们分别指示了单个主成分和多个主成分对原始数据集信息的表达程度。
1.1.1 贡献率假设有m个主成分,第i个主成分的贡献率定义为它对应的特征值在协方差矩阵的全部特征值之和中所占的比重,这个比值越大,说明第i个主成分综合原指标信息的能力越强。设第i个主成分对应特征值σi,则第i个主成分的贡献率Ai为
| $ {A_i} = \frac{{{\sigma _i}}}{{\sum\nolimits_{i = 1}^m {{\sigma _i}} }} $ |
前k个主成分的特征值之和在全部特征值总和中所占的比重,这个比值越大,说明前k个主成分越能全面代表原始数据信息。则前k个主成分的累计贡献率Mk为
| $ {M_k} = \frac{{\sum\nolimits_1^k {{\sigma _i}} }}{{\sum\nolimits_{i = 1}^m {{\sigma _i}} }} $ |
在文中使用的主成分分析程序中,对贡献率和累计贡献率进行了归一化,也就是所有主成分的累计贡献率等于1,所有主成分贡献率的平方和等于1。
1.2 理论接收函数测试文中假设了3组共9个地层模型(表 1),其中:A组为倾斜界面模型,组内各模型唯一变量为倾斜界面的倾角,其中A1模型倾角为3°、A2模型倾倾角为6°、A3模型倾角为9°;B组模型为水平轴各向异性模型,组内各模型唯一变量为各向异性的大小,其中B1模型P波和S波各向异性为3%、B2模型为6%、B3模型为9%;C组为倾斜界面和各向异性共存的模型,各向异性大小不变,为6%,唯一变量为倾斜界面的倾角,其中C1模型倾角为3°、C2模型倾角为6°、C3模型倾角为9°。各地层模型中厚度为0 km的地层表明,该层为半无限空间地层模型,倾斜界面的倾角参数指示地层顶界面。
| 表 1 计算接收函数的地层模型 Table 1 Stratigraphic models used for receiver function modeling |
对每一个地层模型,使用RAYSUM程序(Frederiksen et al,2000)合成理论的R、T、Z三分量地震记录,射线参数设为0.05 km/s,震源脉冲时间设为0.5 s,采样间隔设为0.05 s,共1 024个采样点,360°的反向方位角以10°为间隔观测,共合成37个方位角的接收函数,其中0°和360°方位角接收函数是一致的。将理论合成的R、T、Z三分量地震记录做迭代反褶积(Ligorría et al,1999;Herrmann et al,2004)得到R分量的接收函数,接收函数高斯低通滤波参数设为3.14,大约对应1 Hz拐角频率。对37个不同方位角的R分量接收函数进行主成分分析,同时提取前4个主成分的贡献率和累计贡献率,分析主成分分析方法识别界面倾斜和地壳各向异性的能力。
分析接收函数的时间长度为-5—46.15 s,而在绘图过程中选取-2—8 s的时间段,主要是为了突出Ps转换震相。在实际处理中,不同长度的接收函数主成分分析所得贡献率和累计贡献率不一致(表 2),需特别注意。
| 表 2 理论模型主成分分析前4个主成分的贡献率和累计贡献率 Table 2 The contribution rate and the cumulative contribution rate of the first four principal components |
根据理论模型主成分分析得到的贡献率和累计贡献率(表 2),可得出以下结论。
(1)A组模型为界面倾斜,界面倾斜角度越大,第一主成分贡献率越低,第二主成分贡献率越高,但是第一、第二主成分的累计贡献率也是降低的。
(2)B组模型为各向异性,各向异性越强,第一主成分贡献率越低,第二主成分贡献率越高,但是第一主成分和第二主成分的累计贡献率都达到99%。说明在仅有水平轴各向异性的情况下,第一主成分反映平均地壳结构信息,第二主成分反映各向异性信息,2个主成分可以很好的重构原始R分量接收函数。
(3)C组模型为水平对称各向异性和界面倾斜同时存在,各向异性强度不变,界面倾斜角度逐渐变大,可见第一主成分的贡献率降低,第二主成分的贡献率变大,第一、第二主成分的累计贡献率降低。
张建勇等(2019)认为,径向接收函数的第一主成分包含数据主体信息,反映台站下方一维平均地壳结构特征;而其第二主成分则反映台站下方地壳结构的变化特征。基于本文的分析结果,进一步表明主成分的贡献率和地壳结构的变化特征强度存在一定相关性。莫霍界面倾斜角度越大,各向异性强度越强,表明地壳结构的变化特征越明显,导致第二主成分的贡献率变大,而第一主成分的贡献率变小。
分析第二主成分和第三主成分的贡献率(表 2),可见倾斜界面和水平轴的各向异性不同。对于水平轴各向异性,第二主成分贡献率一般是第三主成分贡献率的5—6倍,而对于倾斜界面,第二主成分贡献率一般是第三主成分贡献率的1—2倍。
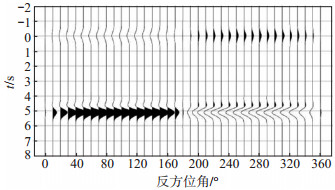
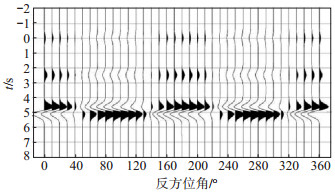
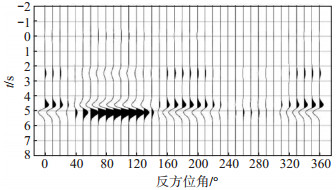
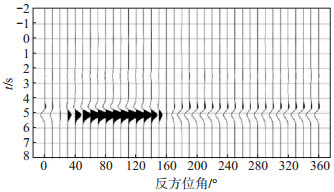
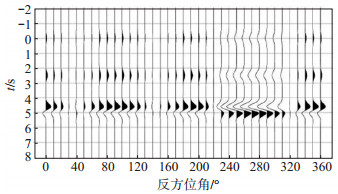
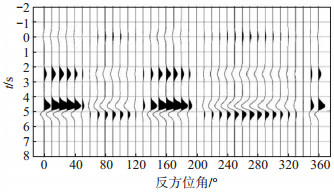
分析第二主成分重构得到的接收函数集可以得出以下结论:对于界面倾斜模型(图 1),两瓣对称,正负极性转换处即为界面走向,其最大振幅的位置则对应界面的倾向(张建勇等,2019);对于水平对称轴各向异性模型(图 2),四瓣对称,负极性信号的中间位置指示了快轴方向;各向异性和倾斜界面共存的情况下(图 3,图 4,图 5,图 6),Ps震相形态随方位角变化复杂,不同的各向异性和倾斜参数组合会导致不一样的变化花样,使用图 1和图 2的判断准则反演参数时会存在误差。如在图 3中,260°—280°反方位角范围内的Ps震相为振幅较小的正极性,而在图 4中,260°—280°反方位角范围内的Ps震相为负极性。C3模型和C1模型各向异性参数是一致的,因为倾斜界面角度的差异,导致第二主成分重构得到的地壳信息不同。C1模型的第二主成分表现出四瓣对称,表现了模型各向异性信息,而C3模型的第二主成分则表现出两瓣花样,表现了界面倾斜特征。分析认为第二主成分表现了不均匀特征。在实际处理中,需要根据震相的周期性决定使用哪个主成分来分析倾斜和各向异性,在倾斜和各向异性均存在的情况下,使用前文所述的倾斜界面走向和各向异性快轴判断准则进行参数反演,结果是不准确的,存在误差。
|
图 1 A2模型第二主成分重构 Fig.1 Reconstruction of the second principal component of the A2 model |
|
图 2 B2模型第二主成分重构 Fig.2 Reconstruction of the second principal component of the B2 model |
|
图 3 C1模型第二主成分重构 Fig.3 Reconstruction of the second principal component of the C1 model |
|
图 4 C3模型第二主成分重构 Fig.4 Reconstruction of the second principal component of the C3 model |
|
图 5 C1模型第三主成分重构 Fig.5 Reconstruction of the third principal component of the C1 model |
|
图 6 C3模型第三主成分重构 Fig.6 Reconstruction of the third principal component of the C3 model |
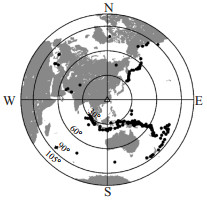
本次使用的地震资料时间跨度较长,时间范围在2007—2017年。选择震中距在30°—95°的5.7级以上远震,截取P波初至前20 s到初至后80 s的波形进行接收函数计算,对事件波形进行去均值、去趋势处理,将原始波形从ZNE坐标旋转到ZRT坐标,带通滤波频率为0.1—2.0 Hz,使用迭代反褶积(Ligorría et al,1999;Herrmann et al,2004)计算接收函数,迭代次数设置为100、接收函数的高斯低通滤波系数设为3.0(该系数对应的拐角频率约为1 Hz),手动挑选接收函数,选择Ps震相较为清晰的接收函数,共得到267条接收函数(图 7)。对挑选完成的接收函数进行校正,参考震中距为67°,消除震中距对Ps震相的到时影响。对校正后的接收函数以10°为间隔,将0°—360°的反方位角分为36个区间,对每个区间的接收函数进行叠加,在每个反方位角区间得到条叠加接收函数,叠加得到的接收函数反方位角设定为参与叠加的区间内接收函数的反方位角的平均值。
|
图 7 接收函数震中分布 Fig.7 Distribution of seismic events |
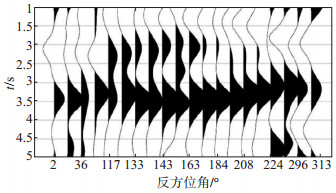
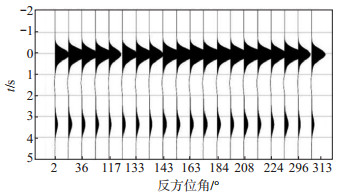
由于某些方位角接收函数缺失,最终得到20条叠加接收函数,对R分量接收函数进行主成分分析。图 8展示了YUG台不同方位角接收函数,可以看到Ps震相随方位角的变化,该特征在图 9中得到更清晰的展示。对R分量接收函数进行主成分分析(图 10—12)和贡献率、累计贡献提取(表 3)。R分量接收函数的第一主成分(图 10)反映了余干台站下方的平均地壳结构,Ps震相的走时为3.4 s。第二和第三主成分重构的接收函数图(图 11,图 12)反映了地壳结构的变化特征。

|
图 8 YUG台不同方位角接收函数 Fig.8 Receiver functions at YUG station in different azimuth directions |
|
图 9 不同方位角接收函数Ps震相放大显示 Fig.9 Enlarged display of Ps Phase receiver functions for different azimuths |
|
图 10 第一主成分重构接收函数 Fig.10 Reconstruction of the first principal component |

|
图 11 第二主成分重构接收函数 Fig.11 Reconstruction of the second principal component |
|
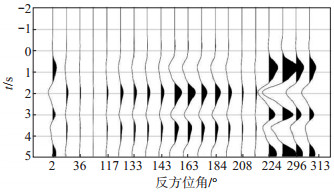
图 12 第三主成分重构接收函数 Fig.12 Reconstruction of the third principal component |
| 表 3 余干地震台不同时间长度接收函数主成分分析前4个主成分的贡献率和累计贡献率 Table 3 The contribution rate and the cumulative contribution rate of the first four principal components of principal component analysis with different time lengths at Yugan Seismic Station |
第二主成分表现出四瓣变化,而第三主成分表现出两瓣变化,再结合第二、第三主成分的贡献率值较为接近,表明余干台站下方同时存在倾斜界面和各向异性,而且各向异性特征更显著。根据第二主成分到时4 s左右震相的变化花样,117°—175°和282°—296°反方位角显示正极性,184°—224°和300°—45°反方位角显示负极性。由于缺失约16个反方位角范围的接收函数,准确判断快轴方向比较困难。根据正演结果,各向异性快轴方向位于负极性信号的中间位置,与正极性中间位置相差90°,仍可以推测余干地震台下方水平轴各向异性的快轴方向大致为NE方向。分析第三主成分到时4 s左右震相的变化花样,只存在正负极性2次转换,45°—117°和224°—282°两个接收函数缺失的位置存在极性转换,而正极性最大值出现在170°左右的反方位角范围。基于以上分析,认为倾斜界面的倾向约170°,走向约80°或260°,位于接收函数缺失的反方位角区间。
对T分量接收函数进行尝试性分析,计算结果显示,T分量接收函数第一主成分的累计贡献率较低(0.58),表明噪声干扰严重。鉴于此,不对T分量接收函数进行主成分分析。对于复杂的地壳结构而言,特别是各向异性和倾斜界面均存在的情况下,通过T分量接收函数主成分分析了解地壳结构变化特征可能比较困难(张建勇等,2019)。
3 结论和讨论基于理论模型测试,认为:利用贡献率和累计贡献率可以定性分析接收函数中地壳结构各种横向不均匀性所占比重,基于主成分分析的第二、第三主成分可在一定程度上分离界面倾斜和各向异性的信息。利用分离后的主成分重构图像分析倾斜界面的走向和各向异性的快轴方向,需要注意判断结果可能存在的误差。
基于余干地震台实际观测数据进行分析,本文认为,该地震台下方倾斜界面和各向异性共存,各向异性产生的不均匀特征强于倾斜界面,占主导作用。倾斜界面的倾向约170°,各向异性快轴方向大致为NE向。目前尚无法使用该方法判断倾斜界面的倾斜角度和各向异性强度信息。
主成分分析方法可以作为分析地壳结构不均匀性的一种补充手段,原理清晰,计算简单,处理方便。目前,主成分分析方法发展快速且应用日益广泛,如加权的主成分分析方法、核主成分分析方法,等等。将这些方法引入接收函数分析应该可以获得更好的效果,需更多研究探索。
文中主成分分析程序来自Eike Rietsch的Seislab工具箱,在此表示感谢。
陈佩. 主成分分析法研究及其在特征提取中的应用[D]. 西安:陕西师范大学,2014.
|
张建勇, 陈凌, 王旭. 2019. 基于接收函数主成分分析法的地壳结构研究[J]. 中国科学:地球科学, 49(5): 822-837. |
赵秀红. 基于主成分分析的特征提取的研究[D]. 西安:西安电子科技大学,2016.
|
Bianchi I, Park J, Agostinetti N P, et al. 2010. Mapping seismic anisotropy using harmonic decomposition of receiver functions:An application to Northern Apennines, Italy[J]. J Geophys Res Solid Earth, 115(B12): B12317. DOI:10.1029/2009JB007061 |
Frederiksen A W, Bostock M G. 2000. Modelling teleseismic waves in dipping anisotropic structures[J]. Geophys J Int, 141(2): 401-412. |
Herrmann R B, Ammon C J. Computer programs in seismology[Z]. St Louis, Missouri:Department of Earth and Atmospheric Sciences, Saint Louis University, 2004.
|
Langston C A. 1979. Structure under Mount Rainier, Washington, inferred from teleseismic body waves[J]. J Geophys Res Solid Earth, 84(B9): 4749-4762. DOI:10.1029/JB084iB09p04749 |
Ligorría J P, Ammon C J. 1999. Iterative deconvolution and receiver-function estimation[J]. Bull Seismol Soc Am, 89(5): 1395-1400. |
Liu H F, Niu F L. 2012. Estimating crustal seismic anisotropy with a joint analysis of radial and transverse receiver function data[J]. Geophys J Int, 188(1): 144-164. |
Owens T J, Zandt G, Taylor S R. 1984. Seismic evidence for an ancient rift beneath the Cumberland plateau, Tennessee:a detailed analysis of broadband teleseismic P waveforms[J]. J Geophys Res Solid Earth, 89(B9): 7783-7795. DOI:10.1029/JB089iB09p07783 |
Zhu L P, Kanamori H. 2000. Moho depth variation in southern California from teleseismic receiver functions[J]. J Geophys Res Solid Earth, 105(B2): 2969-2980. DOI:10.1029/1999JB900322 |
 2020, Vol. 41
2020, Vol. 41

