2. 中国西安 710068 陕西省地震局
2. Shaanxi Earthquake Agency, Xi'an 710068, China
地震的类临界点模型(Main,1995;Ben-Zion et al,2003)近年在地球物理学界讨论较多。该模型将地震的孕育过程看作一种临界点现象(Vere-Jones,1977),在地震学界,认为该现象表现为地震活动持续时间增长及主震周围地震矩加速释放(Accelerating Moment Release,AMR),与凝聚态物理中某些参量在临界点附近的变化相似。采用类临界点模型对震例进行回溯性研究已取得显著成效,并在地震预测领域显现出积极的指导意义和应用潜力(Varnes,1989;Bufe et al,1994;Gross et al,1998;Bowman et al,1998),得到业内广泛关注。国内相关研究成果也逐渐增多,如:蒋长胜等(2004)对中国大陆1978年以来109例MS≥5.7地震事件进行震前矩释放加速现象普遍性讨论,其中55例具有加速特征,23例具有减速特征,其他震例或数据不足或加减速特征不稳定;Jiang等(2006)使用固定的时间尺度和多空间尺度,系统研究中国大陆MS 6.0以上地震事件发生前AMR现象的普遍性问题,发现60%的中强震在发生前存在稳定的地震矩加速释放现象;苗青壮等(2008)研究认为,在震中周边大尺度范围内可检测到矩释放加速现象,而在震中附近较小区域又可检测到矩释放减速现象;李宇彤等(2010)通过研究第五活跃期内中国东北地区5例中强震地震矩释放m值,发现4例地震发生前在震中附近区域出现稳定和集中分布的地震矩释放加速现象;李霞等(2015)利用同样方法对1989年以来华北地区12次MS≥5.0中强地震前的矩加速释放现象进行研究,发现MS 5.6—6.4地震发生前,67%的震例在震中附近出现稳定和集中分布的矩释放加速区域。
本文通过分析地震矩释放的时空特征,对1981年以来鄂尔多斯周缘10次MS≥5.5中强地震进行回溯性检验,窥探该区域中强震发生前地震矩释放的加速特性,进而考察AMR现象在该区中强地震发生前的普遍性意义,以期为今后的震情趋势分析研判提供参考。
1 地震矩加速释放现象Sornette等(1995)研究认为,地震的矩加速释放现象可以作为一种中期地震地球物理异常;一些地震学家(Varnes,1989;Bufe et al,1993, 1994)将重整化群的思想应用到AMR研究中,发展了利用“加速”过程来推测未来地震发生时间的计算方法,称为“离破裂还有多少时间”的分析(time to failure analysis),简称破裂时间分析。这一理论来源于裂纹传播和损伤力学,通过AMR来预测强震的发生时间和震级。国内外已将破裂时间分析方法用于诸多震例,并在一些实际震例的回溯性检验中取得成功(Bufe et al,1993, 1994;Sornette et al,1995;左兆荣等,1996)。地震的破裂时间分析公式(Bufe et al,1993)可表示为
| $ \varepsilon (t) = A + B{({t_{\rm{f}}} - t)^m} $ | (1) |
式中,ε(t)为地震活动性参量,如累积Benioff应变(cumulative Benioff strain,CBS)、标量地震矩、地震辐射能量等;tf为未来主震的发生时间;t为地震前兆事件的时间,且t<tf;A和B为常数;幂指数m称为标度常数,用以定量描述矩释放加减速的大小。由式(1)可知,m值的大小用以描述地震矩释放曲线类型。当m<1时,地震活动性参量表现为加速行为;m>1时,为减速行为;m = 1时,为匀速行为。
在累积Benioff应变计算中,需要根据经验关系(Kanamori,1977)将ML转换为地震矩M0,公式如下
| $ \lg {M_0} = 1.5{M_{\rm{L}}} + 9.05 $ | (2) |
式中,M0的单位是N·m。根据经验关系,地震波能量E由地震矩M0计算得到(Kanamori,1977),表达式为
| $ E = 5.0 \times {10^{ - 5}}{M_0} $ | (3) |
Benioff应变定义为地震波能量的平方根,常数A和B、标度常数m以及地震的发生时刻tf,利用式(1)计算。
此外,国内一些专家做了进一步研究,如:杨文政等(1999, 2000)利用改进的地震活动性加速模型和临界重叠圆方法,检验部分强震的时间、空间和强度,表明该方法是有效的;蒋长胜等(2009)将破裂时间分析方程中的幂指数m作为描述震前加速矩释放程度的参量,在时间—空间—地震序列截止震级构成的三维参数空间(t,r,Mc)内,系统考察2008年3月21日新疆于田MS 7.3地震AMR现象存在的客观性。研究表明,m值随着实际发震时刻的逐渐逼近而减小,AMR现象的空间分布在震前与震中位置有较好对应。这种利用m值的时空演变,研究与大震孕育有关的实际地壳形变过程中应力积累与集中的趋势,寻找未来强震破裂临界区域的方法,也被称为矩释放程度时空扫描方法,实质上是假定实际震中和发震时刻未知,使用固定时空尺度对震前矩释放程度进行扫描,考察中强震前AMR现象的时空分布与实际地震破裂成核点是否吻合。
2 数据选取与处理鄂尔多斯地块位于华北块体西部,与华北平原、青藏、华南活动地块接壤,为山西断陷系、渭河断陷系、银川断陷系和河套断陷系等次级构造单元所围限,内部构造活动性微弱,周边地震活动强烈、复杂(张培震等, 2003, 2013)。近40年内,该地块周缘地区发生了1982年海原MS 5.5、1989年大同MS 5.7、1991年大同—阳高间MS 5.8、1996年乌拉特前旗MS 6.4、1998年张北MS 6.2、2015年阿左旗MS 5.8等地震,对周缘盆地内人口密集的城市群造成较大损失。鄂尔多斯地块周缘未来中强地震将如何发展,是值得深入探索的问题。本文即是以1981年以来鄂尔多斯地块周缘(34°—42°N,104.5°—114.5°E)10次MS≥5.5地震为研究对象,地震参数详见表 1。地震序列使用中国地震台网中心提供的1970年—2019年5月以来的《中国地震月报目录》,该目录由各区域测震台网中心地震目录汇编而成,震级标度ML。
| 表 1 1981年以来鄂尔多斯周缘地区MS≥5.5中强地震参数 Table 1 Parameters of moderate earthquakes with MS ≥ 5.5 in peripheral areas of ordos since 1981 |
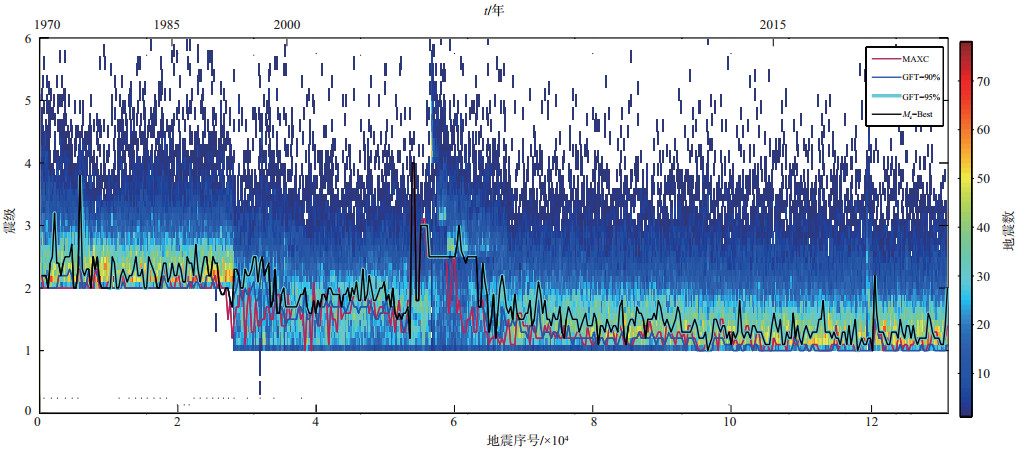
Brehm等(1999)在研究新马德里地震带时,对矩释放加速地震序列的判别提出2个准则,保证了地震事件完整性的同时,排除干扰事件对CBS曲线的影响。鉴于此,采用多方法联合评估与震级—序号方法(冯建刚等,2012)相结合的分析方法,确定鄂尔多斯周缘地区1970—2019年地震的最小完整性震级,结果显示,地震序列的截止震级使用ML 2.5可以保证所用资料的完整性(图 1)。删除与主震震级差为1.2的干扰事件,可有效避免由单个事件造成的假AMR现象。
|
图 1 多方法联合评估鄂尔多斯周缘地区1970—2018年地震Mc值时序变化 Fig.1 The time-series changes of Mc value evaluated by multi-method in ordos peripheral area from 1970 to 2018 |
此外,地震目录余震删除与否尚不统一,对AMR现象研究同样存在争议。因此,有学者在AMR现象研究中,采用折衷方法,即同时给出余震删除前后的结果。如,蒋长胜等(2009)研究指出,余震删除与否对m值计算结果的影响并不明显;李宇彤等(2010)在东北地区中强地震前矩加速释放现象研究中指出,删除余震,m值时空分布与前人研究结果更为接近。因此,文中使用Gardner等(1974)的确定时空窗方法进行余震删除。
3 矩释放程度时空参数利用AMR现象寻找未来中强地震破裂成核点的关键是,在二维m值时空演变中搜索并提取与矩加速释放现象相关的时空参数,即寻找中强地震发生前带有普遍意义的矩释放加速参量m对应的时间与空间参数。因此,使用上文余震删除后的地震目录,将式(1)中的tf固定为目标地震的发震时刻,t取震前1—10 a,以1年为滑动步长;r是以震中为圆心,10 km为步长,在20—300 km范围内的多尺度半径,以此标准选取地震样本,进行累积Benioff应变及辅助参数计算,如幂律拟合的归一化均方差、线性拟合的归一化均方差、反演系数X、ΔBIC(利用贝叶斯信息准则优化的,幂律拟合的归一化均方差与线性拟合的归一化均方差之差)、曲率参数C(Bowman et al,1998)。
为保证计算结果m值的可靠性,删除样本数少于5、ΔBIC<0、Δm>0.5及反演系数X取值在0.01—1的计算结果。
采用矩加速释放现象模型(m<1),绘制鄂尔多斯周缘地区10次中强地震前m值在t—r二维空间等值线分布,结果见图 2,目标地震最低m值对应的时空二维特征尺度见表 1。

|
图 2 鄂尔多斯周缘地区余震删除后10次中强地震前m值在t—r二维空间内的等值线分布 (a)1981内蒙古丰镇MS 5.6地震;(b)1982年宁夏海原MS 5.5地震;(c)1987年宁夏灵武MS 5.5地震;(d)1989年山西大同MS 5.7地震;(e)1991年山西大同—阳高间MS 5.8地震;(f)1996年内蒙古乌拉特前旗MS 6.4地震;(g)1998年河北张北MS 6.2地震;(h)1999年河北张北MS 5.6地震;(i)1999年山西阳高MS 5.6地震;(j)2015年内蒙古阿拉善左旗MS 5.8地震 Fig.2 t-r two-dimensional spatial distribution of m-values for 10 moderate earthquakes after deleting aftershocks in the peripheral of Ordos |
由图 2可见,10次中强地震前AMR或强或弱、或远或近,时空分布错综复杂,主要呈以下特点:①AMR现象较为集中,时空分布连续,如1982年宁夏海原MS 5.5地震和1999年山西—阳高MS 5.6地震;②随着发震时刻逼近,AMR集中区域逐渐向外转移,如1998年河北张北MS 6.2地震和1999年山西阳高MS 5.6地震;③震前AMR现象强弱交替,直至匀速,如1987年宁夏灵武MS 5.5地震;④AMR现象明显,但距发震时刻较远,如1999年河北张北MS 5.6地震;⑤AMR现象距发震时刻较远,其余时间变化不明显,如1989年山西大同MS 5.7地震、1996年内蒙古乌拉特前旗MS 6.4地震和内蒙古阿拉善左旗MS 5.8地震;⑥AMR时空范围较小,如1981年内蒙古丰镇MS 5.6、1989年山西大同MS 5.7和1991年山西大同阳高之间MS 5.8地震。
为了提取鄂尔多斯周缘地区具有相对应用价值的AMR现象时空分布特征尺度,定义矩加速特征q值(李霞等,2015),公式如下
| $ q = \frac{1}{n}\sum\limits_{i = 1}^n {\left[ {1 - {m_i}(t, r)\frac{{{\rm{RM}}{{\rm{S}}_{i - {\rm{nonlinear}}}}(t, r)}}{{{\rm{RM}}{{\rm{S}}_{i - {\rm{linear}}}}(t, r)}}} \right]} $ | (4) |
式中,n为震例数;t、r分别为计算累积Benioff应变曲线的时空参量;mi(t,r)为第i个震例在(t,r)二维空间幂指数m的分布;RMSi-nonlinear(t,r)和RMSi-linear(t,r)分别为第i个震例在(t,r)二维空间幂律拟合归一化均方差和线性拟合归一化均方差;RMSi-nonlinear(t,r) /RMSi-linear(t,r)为曲率参数C;q值实际为各震例反映的带有“优势”的AMR平均时空特征。
鄂尔多斯周缘地区10次中强地震前矩加速释放现象特征值q在t—r二维空间的分布见图 3,其中:矩释放程度时空扫描模型的参数时间窗长t = 6年、扫描半径r = 130 km时,基本符合最佳搜索半径r与震级的线性相关,且与李霞等(2015)的研究结果较为接近。

|
图 3 10次中强震矩加速特征值q在t—r二维空间的分布 Fig.3 t-r two-dimensional spatial distribution of moment accelerating eigenvalue q for 10 moderate earthquakes |
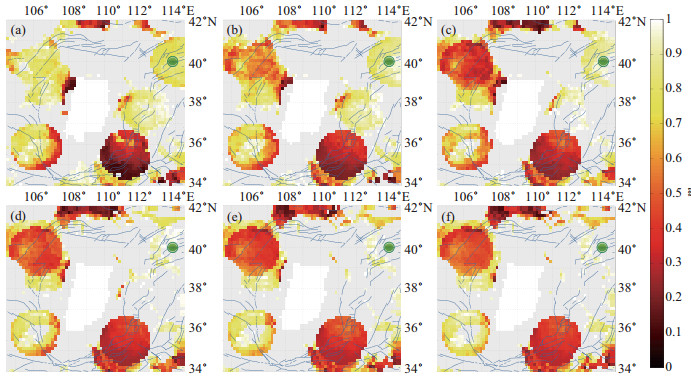
按照地震的临界性概念,通常认为主震发生前震中周围介质形成临界区域,强震的发生将临界状态破坏,并使之恢复到背景水平。若主震震中在临界点附近,主震发生前即可通过一定空间范围的扫描搜寻震中位置(李宇彤等,2010)。本研究利用矩释放程度时空扫描模型参数(t = 6年、r =130 km),对该区域1981以来10次MS≥5.5中强地震分别进行震前12个月、9个月、6个月、3个月、1个月及震时的m值空间扫描(为了降低计算复杂度,提供更快速有效的处理,采用基于Levenberg-Marquardt法的非线性回归对非线性模型中的参数进行求解,具体迭代步数设定为 10 步)。通过对AMR现象空间分布结果分析,发现随着发震时刻的临近,在破裂成核点附近,矩加速释放m值表现为减弱或增强,且m值增强震例显示出集中、持续的特点。具体而言,震中及附近在震前1年呈现出以下4方面特征:①震中AMR现象在逐渐消失,见图 4,2个震例分别是1981内蒙古丰镇MS 5.6地震和1991年山西大同—阳高间MS 5.8地震,持续时间分别为3个月和6个月;②震中AMR现象逐渐出现,见图 5,4个震例分别是1982年宁夏海原MS 5.5地震、1987年宁夏灵武MS 5.5地震、1998年河北张北MS 6.2地震和1999年山西阳高MS 5.6地震,持续时间为3—6个月;③震中AMR现象持续存在,直至发震,见图 6,2个震例分别是1989年山西大同MS 5.7地震和1999年河北张北MS 5.6地震;④震中周围出现类椭圆形AMR现象区域,甚至有的内部出现AMR现象,见图 7,2个震例分别是1996年内蒙古乌拉特前旗MS 6.4地震和2015年内蒙古阿拉善左旗MS 5.8地震,持续时间近12个月。图 4—图 7中绿色圆表示地震发生位置。
|
图 4 1991年3月26日山西大同—阳高间MS 5.8地震m值分布 (a)震前12个月;(b)震前9个月;(c)震前6个月;(d)震前3个月;(e)震前1个月;(f)震时 Fig.4 Distribution of m values for the Datong-Yanggao MS 5.8 earthquake in Shanxi on March 26, 1991 |
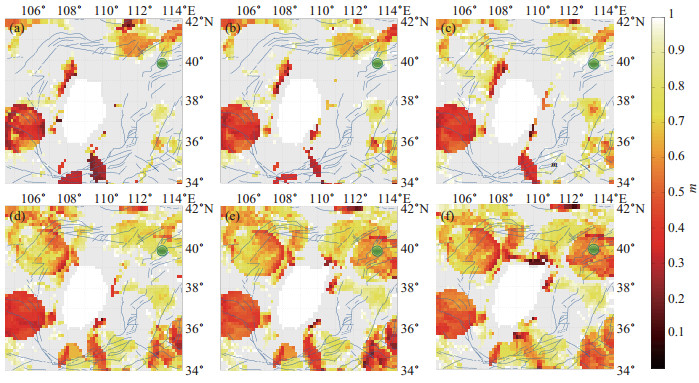
|
图 5 1999年11月1日山西阳高MS 5.6地震m值分布 (a)震前12个月;(b)震前9个月;(c)震前6个月;(d)震前3个月;(e)震前1个月;(f)震时 Fig.5 Distribution of m values for the Yanggao MS 5.6 earthquake in Shanxi on November 1, 1999 |
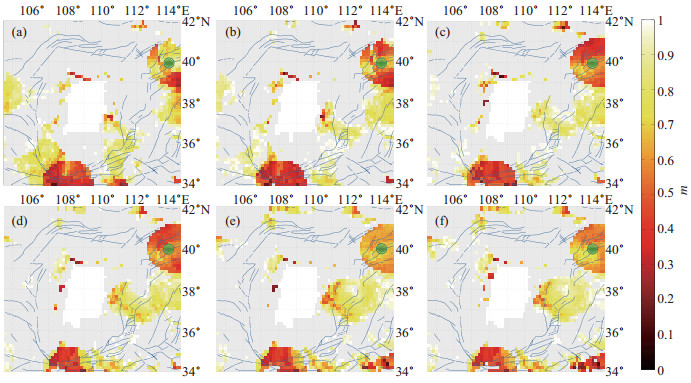
|
图 6 1989年10月18日山西大同MS 5.7地震m值分布 (a)震前12个月;(b)震前9个月;(c)震前6个月;(d)震前3个月;(e)震前1个月;(f)震时 Fig.6 Distribution of m values for the Datong MS 5.7 earthquake in Shanxi on October 18, 1989 |
|
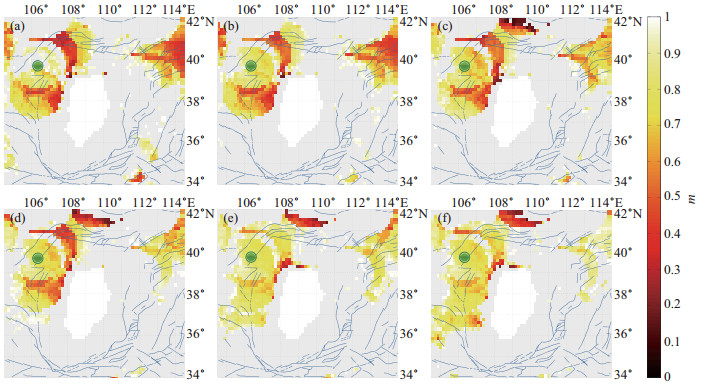
图 7 2015年4月15日内蒙古阿拉善左旗MS 5.8地震m值分布 (a)震前12个月;(b)震前9个月;(c)震前6个月;(d)震前3个月;(e)震前1个月;(f)震时 Fig.7 Distribution of m values for MS 5.8 earthquake in Alxa Left Banner, Inner Mongolia on April 15, 2015 |
以上AMR现象与发震地点时空上的吻合,说明地震的孕育过程和矩加速释放现象的物理过程具有密切关联。与此同时,以1991年山西大同—阳高间MS 5.8地震前1年的矩释放程度空间扫描为例(图 4),可知震前1年以来,鄂尔多斯周缘存在3个集中、持续的AMR低m区域(东北缘、西南缘及东南缘),而地震却发生在东北缘,说明AMR方法在地震预测方面具备发展可挖掘性的同时,仍存在诸多未知因素。
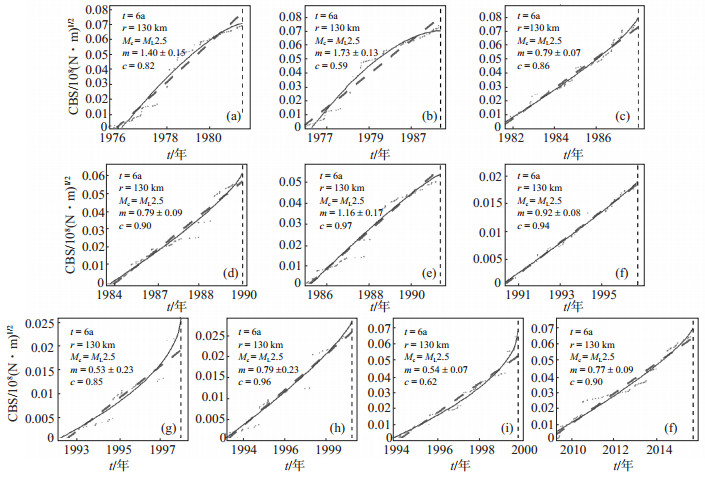
为进一步考察鄂尔多斯周缘中强震前破裂成核点附近AMR情况,分别以实际震中为圆心,采用矩释放程度时空扫描模型(即t = 6年、r = 130 km),分别计算10次MS≥5.5地震破裂成核点附近累积Benioff应变能释放情况,相应的累积Benioff应变释放曲线和非线性拟合见图 8(各图中灰色圆点为震前的累积Benioff应变数据点,实曲线为Benioff应变非线性拟合曲线,虚线为线性拟合结果,垂直细虚线标出主震的发震时刻。
|
图 8 震前破裂成核点的累积Benioff应变释放曲线 (a)1981年内蒙古丰镇MS 5.6地震;(b)1982年宁夏海原MS 5.5地震;(c)1987年宁夏灵武MS 5.5地震;(d)1989年山西大同MS 5.7地震;(e)1991年山西大同—阳高间MS 5.8地震;(f)1996年内蒙古乌拉特前旗MS 6.4地震;(g)1998年河北张北MS 6.2地震;(h)1999年河北张北MS 5.6地震;(i)1999年山西阳高MS 5.6地震;(j)2015年内蒙古阿拉善左旗MS 5.8地震 Fig.8 Cumulative Benioff strain release curves at rupture nucleation points before earthquakes |
从破裂成核点附近累积Benioff应变曲线(图 8)来看,仍有3例不具备矩加速释放特征,说明矩加速释放现象并不是中强地震孕育的唯一特征。尽管如此,由表 1清楚可见,10次震例中仅有3例在地震破裂成核点附近表现为减速特征,剩余7例均表现为加速特征,占总数的70%,因此认为鄂尔多斯周缘地区MS≥5.5中强地震前矩加速释放现象具有一定的普遍性。
5 结论和讨论利用矩加速释放现象m值,对1981年以来鄂尔多斯周缘地区10次MS≥5.5地震前的AMR现象进行回溯性检验,结果如下。
(1)通过对m值在二维时空的扫描分析,提取鄂尔多斯周缘地区中强地震前AMR现象的时空尺度,即矩释放程度时空扫描模型参数,在时间窗长t = 6年、扫描半径r =130 km的情况下,AMR现象具有普遍性和应用潜力。
(2)利用得到的矩释放程度时空扫描模型参数,对研究区震例进行震前1年至震时,依次递减3个月的空间扫描。结果显示,随着发震时刻的临近,破裂成核点附近,矩加速释放m值表现或逐渐减弱、或逐渐增强、或持续增强、或震中周边出现类椭圆形AMR区域,甚至有的内部出现AMR现象。这些特征与实际震中有较好的对应关系。
(3)考察震前破裂成核点附近的累积Benioff应变释放情况,可知10次震例中有7例在震中区存在AMR现象,与空间扫描结果基本一致,说明鄂尔多斯周缘地区MS≥5.5中强地震前AMR现象存在一定的普遍性,AMR现象与地震孕育具有一定关联。
综上所述,地震孕育过程并非AMR过程那么简单,其复杂性主要体现在震前AMR现象持续增强,但增强区域不唯一,给破裂成核点的判断带来一定干扰。因此,应用矩加速时空扫描方法对未来中强地震破裂成核点的判断,仅是地震预测方法的考量之一,存在一定潜力的同时,不可否认其不确定性,仍需结合其他地震学方法进行综合分析。
需要指出的是,在矩释放程度时空扫描模型参数地提取过程中,对不同震例带有的“优势”AMR时空特征参数进行归一化处理,可能会带入与地震孕育无关的时空信息。因此,如何可靠地选取时空尺度参数,需在后续研究中对震例展开逐一深入地研究和筛选。
中国地震局地球物理研究所蒋长胜博士提供AMR及时空参数计算程序,东北师范大学数学与统计学院孙佳宁博士在程序调试过程中给予悉心指导,在此深表谢意!
冯建刚, 蒋长胜, 韩立波, 等. 2012. 甘肃测震台网监测能力及地震目录完整性分析[J]. 地震学报, 34(5): 646-685. DOI:10.3969/j.issn.0253-3782.2012.05.006 |
蒋长胜, 吴忠良, 史勇军. 2004. 中强震前地震活动矩释放加速现象(AMR)的普遍性问题[J]. 中国地震, 20(2): 119-125. DOI:10.3969/j.issn.1001-4683.2004.02.001 |
蒋长胜, 吴忠良. 2009. 强震前的"加速矩释放"(AMR)现象:对一个有争议的地震前兆的回溯性震例研究[J]. 地球物理学报, 52(3): 691-702. |
李霞, 蒋长胜, 闫德桥, 等. 2015. 1989年以来华北地区中强震前地震矩加速释放空间扫描特征的研究[J]. 地震研究, 38(3): 359-369. DOI:10.3969/j.issn.1000-0666.2015.03.004 |
李宇彤, 蒋长胜. 2010. 东北第五活跃期中强震前的矩释放空间扫描特征研究[J]. 地震学报, 32(6): 680-695. |
苗青壮, 蒋海昆. 2008. 地震临界现象及相关尺度增长定量检测方法研究综述[J]. 地震, 28(2): 79-86. DOI:10.3969/j.issn.1000-3274.2008.02.009 |
杨文政, 马丽. 1999. 地震活动加速模型及其在中国的应用[J]. 地震学报, 21(1): 32-41. DOI:10.3321/j.issn:0253-3782.1999.01.005 |
杨文政, Jones D V, 马丽, 等. 2000. 一个关于临界地震的临界区域判别的方法[J]. 地震, 20(4): 28-38. |
张培震, 邓启东, 张国民, 等. 2003. 中国大陆的强震活动与活动地块[J]. 中国科学:地球科学, 33(Z1): 12-20. |
张培震, 邓启东, 张竹琪, 等. 2013. 中国大陆的活动断裂、地震灾害及其动力过程[J]. 中国科学:地球科学, 43(10): 1607-1620. |
左兆荣, 张国民, 吴建平. 1996. 1976年云南龙陵7.4级地震序列分析[J]. 地球物理学报, 39(5): 653-659. DOI:10.3321/j.issn:0001-5733.1996.05.008 |
Ben-Zion Y, Eneva M, Liu Y F. 2003. Large earthquake cycles and intermittent criticality on heterogeneous faults due to evolving stress and seismicity[J]. J Geophys Res Solid Earth, 108(B6): 2307. |
Bowman D D, Ouillon G, Sammis C G, et al. 1998. An observational test of the critical earthquake concept[J]. J Geophys Res Solid Earth, 103(B10): 24359-24372. DOI:10.1029/98JB00792 |
Brehm D J, Braile L W. 1999. Intermediate-term earthquake prediction using the modified time-to-failure method in Southern California[J]. Bull Seismol Soc Amer, 89(1): 275-293. |
Bufe C G, Varnes D J. 1993. Predictive modeling of the seismic cycle of the Greater San Francisco Bay Region[J]. J Geophys Res Solid Earth, 98(B6): 9871-9883. DOI:10.1029/93JB00357 |
Bufe C G, Nishenko S P, Varnes D J. 1994. Seismicity trends and potential for large earthquakes in the Alaska-Aleutian region[J]. Pure Appl Geophys, 142(1): 83-99. DOI:10.1007/BF00875969 |
Gardner J K, Knopoff L. 1974. Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian?[J]. Bull Seismol Soc Amer, 64(5): 1363-1367. |
Gross S J, Rundle J B. 1998. A systematic test of time-to-failure analysis[J]. Geophys J Int, 133(1): 57-64. |
Jiang C S, Wu Z L. 2006. Benioff strain release before earthquakes in China:accelerating or not?[J]. Pure Appl Geophys, 163(9): 1965-1976. DOI:10.1007/s00024-006-0107-1 |
Kanamori H. 1977. The energy release in Great earthquakes[J]. J Geophys Res, 82(B20): 2981-2987. |
Main I G. 1995. Earthquakes as critical phenomena:implications for probabilistic seismic hazard analysis[J]. Bull Seismol Soc Amer, 85(5): 1299-1308. |
Sornette D, Sammis C G. 1995. Complex critical exponents from renormalization group theory of earthquakes:implications for earthquake predictions[J]. J Phys I, 5(5): 607-619. |
Varnes D J. 1989. Predicting earthquakes by analyzing accelerating precursory seismic activity[J]. Pure Appl Geophys, 130(4): 661-686. DOI:10.1007/BF00881603 |
Vere-Jones D. 1977. Statistical theories of crack propagation[J]. Math Geol, 9(5): 455-481. DOI:10.1007/BF02100959 |
 2020, Vol. 41
2020, Vol. 41

