弹性波在传播过程中遇到不均匀介质会产生散射波,即尾波。20世纪20年代,Jeffreys(1929)将尾波用于地震学研究,之后,Aki(1969)用散射模型解释了尾波的形成,Sato(1977)等对Aki提出的尾波计算方法进行了修正。
Q值是衡量地球介质对地震波衰减(Qt)的跟本物理参数之一,是描述地壳介质非均匀程度的确定性指标。Q值大小及其对频率的依赖程度反映了介质的非均匀性和非弹性特征(Roecker et al,1982),与区域构造活动及地震活动性密切相关(Chouet,1979;Singh et al,1983;Jin et al,1985),被广泛应用于地震预报。观测台站记录到延迟的散射波,计算其尾波Q值,可得到附近区域的Q值变化特征,同理,计算一个区域所有台站的尾波Q值,即可知该区域Q值变化特征(刘芳等,2007)。计算尾波Q值主要使用单次散射模型,有Sato模型和Aki模型2种,差别在于:Aki单次回转散射模型的架设源点和接收点在同一点,未考虑极化和能量在三分量上的分割;Sato各向同性单次散射模型源点和接收点是分开的(王伟君等,2004),是Aki模型普遍化的推广,可认为多次散射模型的一阶近似,物理解释更接近实际。
文中采用Sato、Aki模型,选取2016年3月至2019年6月内蒙古东北部地区发生的部分地震,计算并分析该区域Q值与构造活动及地震活动性的关系,分析其分布特征,并与马云生等(1995)、贺永忠等(2012)的研究结果进行对比,从而对该区域介质衰减特征及区域地震活动性进行客观评估。
1 研究区地质构造与地震活动特征内蒙古呈狭长分布,东西跨度大,横跨中国西北、华北、东北3个地区,地质构造复杂。内蒙古东北部地区(46.90°—53.50°N,115.50°—126.10°E)包含呼伦贝尔全部地区及兴安盟北部部分区域,主要为前中生代地质构造格局,断裂带分布密集。
本研究区域涉及作为一级大地构造单元的天山—兴安岭断褶系,二级构造单元的北兴安岭端着带、南兴安岭断褶带和额尔古纳断褶带。各级构造单元各具特点,构造特征呈现差异性。区内断裂带以NNE向、近EW向和NW向为主,其中:NNE向和近EW向断裂一般为深大断裂,控制了区内大的地质构造格局;NW向断裂与NNE向断裂相比,活动时代较新,地震活动与NW向和NN向断裂有关(张晖,2013)
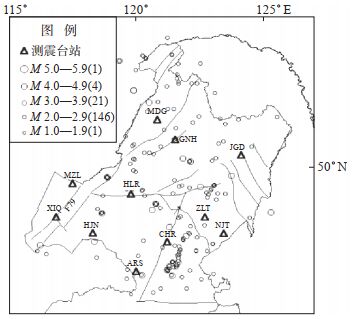
内蒙古东北部地区有2个断裂带附近区域地震活动性较强:①扎赉诺尔断裂,见图 1中F79。该断裂带位于海拉尔盆地西侧,是海拉尔沉降带与额尔古纳隆起带的分界断裂,1979年2月6日在附近区域(新巴尔虎右旗)发生5.0级以上地震,近几年发生一系列小震弱震活动;②绰尔河断裂带,见图 1中F70。在该断裂带东侧,沿断裂带NNE方向小震密集,呈条状分布。
|
图 1 内蒙古东北部地区断裂、地震台站及2016—2019年地震分布 Fig.1 Distribution of faults, seismic stations, and earthquakes from 2016 to 2019 in northeastern Inner Mongolia |
内蒙古东北部地区(46.90°—53.50°N,115.50°—126.10°E)共分布测震台站11个,各台站基本参数见表 1,台站分布见图 1。
| 表 1 东北部区域11个台站基本参数 Table 1 Basic parameters of 11 stations in the northeastern area |
选取11个测震台站2016年3月—2019年5月记录的地震波形数据,统计可知:内蒙古东北部及周边地区在此时段内共发生地震925次,其中ML ≥ 2.0地震事件170余次(图 1),最大地震为2018年5月28日吉林松原ML5.6地震,并从中选取133次记录清晰、噪声值低、尾波衰减时间相对长的地震事件,利用Sato、Aki模型分别进行尾波Q值计算。
3 方法原理尾波由S波的散射波组成,测量S波品质因子QS的方法有:①利用S波振幅随距离衰减的性质,使用Aki(1980)尾波规一法,消除震源辐射方向性,求取平均值,适用于分布在一定范围内多方位、多次地震;②利用尾波振幅随时间衰减的性质,使用单次散射的Aki(1975)模型和Sato(1977)模型,有适当长度的单台尾波记录即可获得结果。
3.1 Aki单次散射模型计算原理(Aki,1975)通过以某频率为中心频率的一定带宽滤波器滤波后,尾波振幅可以表述为
| $ A(f,t) = S(f){t^u}{{\rm e}^{{\rm \pi} ft/Q(f)}} $ | (1) |
式中,S(f)为震源因子;t为发震时刻算起的地震波流逝时间;u为常数,近震时u = 1;Q(f)为对应于中心频率点f的尾波Q值;A(f,t)是对应t时刻一个采样周期的幅度最大值。对式(1)两边取自然对数,整理可得
| $ {\rm \ln} (A(f,t){t^u}) = {\rm \ln} S(f) - at $ | (2) |
式(2)表明,ln(A(f,t)tu)与t存在线性关系,拟合可得a = -πf/Q(f),由此可得对应频点的尾波Q值,即
| $ Q(f) = - {\rm \pi} f/a $ | (3) |
在一定频率下,尾波振幅与时间的函数关系可表示为
| $ F(t) = {\rm \lg} \{ {[{A_{\rm C}}(t)/{A_{\rm S}}]^2}{K^{ - 1}}(a)\} = C(f) - b(t - {t_{\rm S}}) $ | (4) |
式中:AS为S波最大振幅,AC(t)为流逝时间t附近的尾波均方根振幅,K(a)为依赖于时间的传播因子。
| $ K(a) = 1/a{\rm \ln} [(a + 1)/(a - 1)] $ | (5) |
| $ {A_{\rm C}}(t) = {(A_T^2 - A_n^2)^{1/2}} $ | (6) |
式中,AT为所取时间窗内地震波均方根;An为P波到达前适当时间段记录的均方根,用以进行地震波噪声校正;a = t/tS,其中tS为S波流逝时间;C(f)为与频率有关的影响因子,对相同地震的同一频率,C(f)为常数;拟合F(t)与(t - tS)的线性关系,得到斜率b,b与QC的关系为
| $ b = (2{\rm \pi} f{\rm \lg e})/{Q_{\rm C}} $ | (7) |
由各个频率点的QC值,拟合得到QC(f)。
| $ {Q_{\rm C}}(f) = {Q_0}{f^\eta } $ | (8) |
其中,Q0为对应频率1 Hz的尾波衰减参数,η为Q值对应频率的依赖性指数。
4 Q值计算 4.1 计算步骤选取记录清晰、噪声值低、尾波衰减时间相对长,符合计算要求的133条地震事件进行计算,采用6阶Butterworth带通滤波器,将频率以[f±(1/3)f]进行带宽滤波。以1 Hz为间隔,得到4—18 Hz范围内15个频点数据,设均方根振幅窗长2 s,时间步长0.5 s,流逝时间60—80 s,选取S波到时的2倍走时开始尾波计算,选择P波初动前3 s的平均噪声信号作为背景噪声。
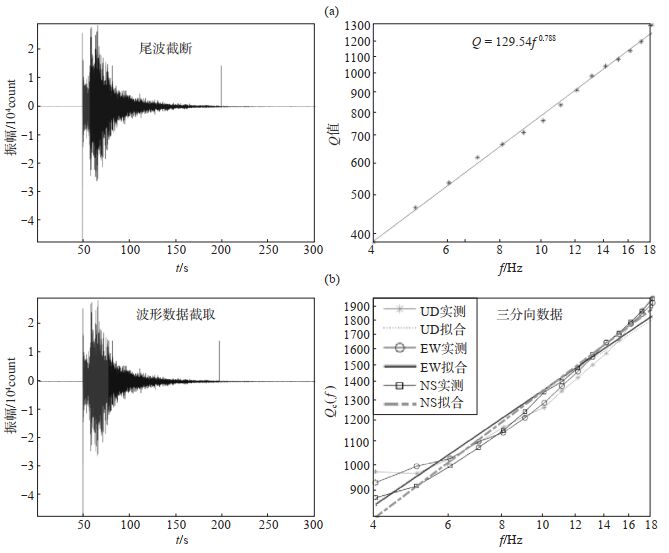
以绰尔地震台记录的2018年2月26日内蒙古扎兰屯ML 3.6地震为例,采用Sato、Aki模型,分别计算尾波Q值,结果见图 2,其中(a)图给出Sato模型尾波截取区间及4—18 Hz共15个频点的Q值分布;(b)图给出Aki模型尾波截取区间及4—18 Hz共15个频点的Q值分布。
|
图 2 2018年2月26日内蒙古扎兰屯ML 3.6地震基于Sato、Aki模型的计算实例 (a)Sato模型;(b)Aki模型 Fig.2 Calculation results of the Zhalantun ML 3.6 earthquake on 26 February 2018 using the Sato and Aki models |
由图 2可见,采用Sato、Aki模型计算同一地震事件,各频点Q值均呈线性分布,表明拟合的Q值结果具有可靠性。
4.2 尾波Q值拟合结果采用Sato、Aki模型,分别计算内蒙古东北部地区11个台站的Q0值,拟合得到各台站尾波Q0值、依赖指数η及二者标准偏差,结果见表 2、表 3,其中表 2为Sato模型的计算结果,表 3为Aki模型的计算结果。
| 表 2 基于Sato模型台站Q值计算结果 Table 2 Calculation results of coda wave Q values in every station based on the Sato model |
| 表 3 基于Aki模型台站Q值计算结果 Table 3 Calculation results of coda wave Q values in every station based on the Aki model |
由表 2可知,采用Sato模型计算尾波Q值,Q0值主要集中在60—70,依赖指数η主要集中在0.8—0.9,莫尔道嘎台Q0值最高,为71.44,呼吉日诺尔台Q0值最低,为41.37。由表 3可知,采用Aki模型计算尾波Q值,Q0值主要集中在200—300,依赖指数η主要集中在0.6—0.7,莫尔道嘎台Q0值最高,为306.5,阿尔山台Q0值最低,为186.5。
采用单一台站记录的波形事件计算尾波Q值,可得到该台站附近区域Q值变化,采用所有台站计算,便可得到本区域Q值变化特征。利用数学统计原理,分析计算所得尾波Q值,得到研究区域Q值数据与15个频率点的拟合关系,结果见表 4、图 3,其中图 3(a)为Sato模型拟合结果,图 3(b)为Aki模型拟合结果。
| 表 4 内蒙古东北部地区Q值拟合结果 Table 4 Q value fitting results in the Northeastern Inner Mongolia area |

|
图 3 内蒙古东北部地区Q值拟合 (a)Sato模型拟合结果;(b)Aki模型拟合结果 Fig.3 Q value fitting in the Northeastern Inner Mongolia area |
根据表 1、图 3所示数据结果,给出2种模型下QC值与对应频率的依赖关系,具体如下。
Sato模型QC值与对应频率的依赖关系为
| $ {Q_{\rm C}}(f) = (64.11 \pm 29.15){f^{(0.8914 \pm 0.0772)}} $ | (9) |
Aki模型QC值与对应频率的依赖关系为
| $ {Q_{\rm C}}(f) = (258.4 \pm 65){f^{(0.6815 \pm 0.1435)}} $ | (10) |
基于Sato模型的计算结果与翟浩等(2019)对附近地区的研究结果相比,地震事件数增多,分析结果接近,误差较小,证明本次所得计算结果较为可靠。
5 结论与讨论采用Sato、Aki模型,分别拟合内蒙古东北部地区Q值,结果认为:①各地震台站计算的区域Q值存在明显差异,且Aki模型计算所得Q值较大;②基于2种模型计算的各地震台Q值分布存在一致性,提高了研究区域Q值分布的可信性;③Q值分布具有北部偏高、南部偏低的特点;④研究区Q值最大值均在莫尔道嘎台,最小值则在阿尔山台、呼吉日诺尔台;⑤Q0值与依赖性指数η大致成反比关系,与师海阔等(2016)的研究结果一致。
本研究将内蒙古东北部地区11个台站按区域进行划分,其中:①北部为以根河台、满洲里台、根河台,地震活动相对稳定,拟合得到的Q值偏高;②中部为西旗台、海拉尔台、呼吉日诺尔台,地处扎赉诺尔断裂(见图 1中F79断裂)附近,曾于1979年2月6日在附近区域(新巴尔虎右旗)发生5.0级以上地震,且近几年该区域发生一系列弱震活动,拟合Q值偏低;③南部为加格达奇台、扎兰屯台、那吉屯台、绰尔台、阿尔山台,地处绰尔河断裂带(见图 1中F70中)附近,该断裂带东侧沿NNE方向小震密集,呈条状分布,拟合Q值偏低。
综上所述,尾波Q值高低分布与地震活动性及地质构造有关,即:地震活动频繁程度越高的地区Q值越低,反之Q值越高;在构造活动强烈地区,地下介质均匀程度低,地震波经过时能量损耗大、衰减快,Q值较低;在构造活动较稳定地区,地下介质均匀程度高,地震波经过时衰减慢,Q值较高。
贺永忠, 师海阔, 朱新运, 张立恒. 2012. 利用两种模型对宁夏及邻区尾波Q值进行对比研究[J]. 大地测量与地球动力学, 32(Z1): 10-17. |
刘芳, 苗春兰, 高艳玲. 2007. 内蒙古中西部地区尾波Q值研究[J]. 地震, 27(2): 72-80. DOI:10.3969/j.issn.1000-3274.2007.02.009 |
马云生, 张天中, 张焕生. 1995. 北京及其周围地区尾波Q值分布特征的研究[J]. 地震学报, 17(1): 448-458. |
师海阔, 曾宪伟, 田小慧, 等. 2016. 利用Sato模型研究宁夏及邻区尾波Q值分布特征[J]. 地震地磁观测与研究, 37(1): 22-29. |
王伟君, 刘杰. 2004. 1999年岫岩地震序列尾波Qc的变化过程[J]. 地震, 24(4): 37-44. |
翟浩, 王树波, 曹梦娜. 2019. 基于Sato模型的内蒙古东北部地区尾波Q值[J]. 地震地磁观测与研究, 40(1): 48-52. |
张晖.内蒙古地区波速比变化特征的研究[D].兰州: 中国地震局兰州地震研究所, 2013: 12-14. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2410353
|
Aki K. 1969. Analysis of the seismic coda of local earthquakes as scattered waves[J]. J Geophys Res, 74(2): 615-631. DOI:10.1029/JB074i002p00615 |
Aki K, Chouet B. 1975. Origin of Coda waves:source, attenuation, and scattering effects[J]. J Geophys Res, 80(23): 3322-3342. DOI:10.1029/JB080i023p03322 |
Aki K. 1980. Scattering and attenuation of shear waves in the lithosphere[J]. J Geophys Res Solid Earth, 85(B11): 6496-6504. DOI:10.1029/JB085iB11p06496 |
Chouet B. 1979. Temporal variation in the attenuation of earthquake coda near Stone Canyon, California[J]. Geophys Res Lett, 6(3): 143-146. DOI:10.1029/GL006i003p00143 |
Domínguez T, Rebollar C J, Fabriol H. 1997. Attenuation of coda waves at the Cerro Prieto Geothermal Field, Baja California, Mexico[J]. Bull Seismol Soc Am, 87(5): 1368-1374. |
Jeffreys. 1929. On the transverse circulation in streams[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 25(1): 20-25. DOI:10.1017/S0305004100018508 |
Jin A S, Cao T Q, Aki K. 1985. Regional change of coda Q in the oceanic lithosphere[J]. J Geophys Res Solid Earth, 90(B10): 8651-8659. DOI:10.1029/JB090iB10p08651 |
Roecker S W, Tucker B, King J, et al. 1982. Estimates of Q in central Asia as a function of frequency and depth using the coda of locally recorded earthquakes[J]. Bull Seismol Soc Am, 72(1): 129-149. |
Sato H. 1977. Energy propagation including scattering effects Single isotropic scattering approximation[J]. Journal of Physics of the Earth, 25(1): 27-41. |
Singh S, Herrmann R B. 1983. Regionalization of crustal coda Q in the continental United Stated[J]. J Geophys Res Solid Earth, 88(B1): 527-538. DOI:10.1029/JB088iB01p00527 |
 2020, Vol. 41
2020, Vol. 41

