地震定位精度是评估地震台网监测能力的一项重要指标,受地震台站分布、地壳结构速度模型、震相拾取精度、定位算法等多种因素的影响。直接对地震波形进行相关分析,可以减少地区结构速度模型等因素的影响,可以有效评估地震台网定位质量和震相拾取精度。早在10年前,王小龙(2007)利用27个测震台站地噪声计算了三峡库区重庆段的地震监测能力,王同军等(2016)结合邻省地震台站重新计算了其监测能力,随着数字地震台网的发展,使用波形互相关技术和重复地震评估地震台网定位精度的技术引起人们越来越多的关注(Rubin,2002;Schaff et al,2004;蒋长胜等,2005;董非非等,2016;马晓静等,2017)。
重复地震概念于20世纪60年代被提出,目前尚无统一定义(李宇彤等,2011),Schaff等(2004)将重复地震定义为:被至少一个台站记录到,且波形相关系数不小于0.8的地震对事件。波形相关意义的重复地震通常可定义为:在地震台站记录的地震事件波形资料中,具有强相关性的地震对(李宇彤等,2008)。重复地震对的特点有:波形高度相似,震级相近,震源机制解一致等(董非非等,2016)。
中国地震学者由重复地震给出中国地震台网的定位误差平均在10 km的数量级(蒋长胜等,2005),首都圈数字地震台网整体的水平定位误差约为5 km,Pg、Sg震相人工拾取误差为0.7 s和1.4 s(蒋长胜等,2008)。近几年,董非非等(2016)、马晓静等(2017)、孟真等(2019)分别在江西、广东、四川地区利用重复地震评估区域地震台网定位精度和震相拾取误差,得到:江西地区22%的重复地震水平距离在1 km以内,65%的重复地震水平距离在1—5 km;广东地区90%的重复地震水平距离在1.5 km以内,约80%的重复地震Pg、Sg走时差在0.3 s内;四川龙门山断裂带周缘的水平定位误差约为2.8 km,垂直定位误差约为10 km。以上结果与蒋长胜等(2005)的结果相比,得到较大提高,可能是数字地震观测资料大量积累、测震台站加密观测、定位方法改善等所致。
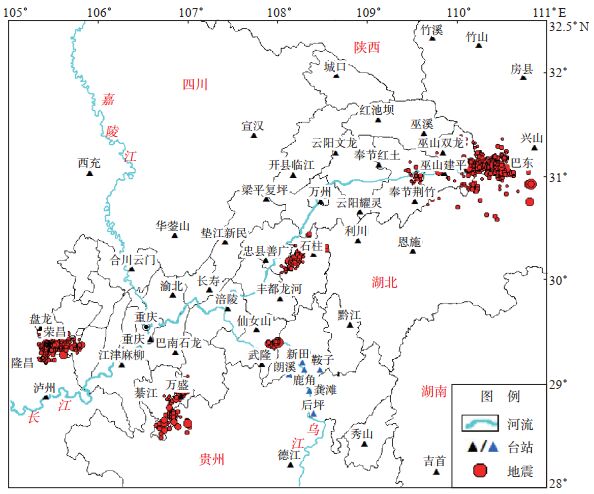
1 资料选取重庆数字地震台网现有36个测震台站,并从周边省份接入17个共享台站,台站分布见图 1。其中重庆台网包括1个国家台、14个区域台、15个“三峡”项目台站、6个企业台站,主要配备宽频带和短周期地震计,采样率均为100 Hz。从地震台站布局和分布(图 1)来看,渝东北地区分布三峡项目台站(在图 1中以4个汉字标注),渝东南地区分布彭水电站企业台(图 1中蓝色三角形),本地台网台站分布表现出东密西疏的现象。
|
图 1 地震台站和震中分布 Fig.1 Distribution of seismic stations and epicenters |
自2008年数字化改造以来,重庆数字地震台网积累了大量重庆及邻区(28°—32.5°N,105°—111°E)地震事件和观测报告,地震分布见图 1,发现地震主要分布在荣昌—隆昌区、綦江区、武隆区、石柱区、巫山—巴东区(陈凯等,2019)。选取2010年1月1日至2017年12月31日地震波形资料和观测报告,选择以上5个地震多发区为研究区,得到1 251个ML≥1.5地震进行波形互相关分析,以至少被2个台站同时记录且各台波形互相关系数(cc)不小于0.8的地震对为标准,挑选符合条件的重复地震对,结合相关地震观测报告,对重庆数字地震台网震相拾取误差和定位精度进行评估,为将来新建台站布设和定位精度改善提供一定参考依据。
2 重复地震识别 2.1 计算方法计算地震事件波形的互相关系数,可有效识别重复地震。则互相关系数γ为
| $ \gamma {\rm{ = }}\frac{{\sum {\left[ {{f_1}(t) - \overline {{f_1}(t)} } \right]\left[ {{f_2}(t) - \overline {{f_2}(t)} } \right]} }}{{\sqrt {\sum {{{\left[ {{f_1}(t) - \overline {{f_1}(t)} } \right]}^2} + \sum {{{\left[ {{f_2}(t) - \overline {{f_2}(t)} } \right]}^2}} } } }} $ | (1) |
式中,f1(t)和f2(t)分别为同一台站记录的2次地震事件选定波列,
在进行波形互相关计算之前,人工剔除震相不清晰的地震事件,选择波形清楚的地震,最终得到所选的1 251次地震事件。在只选择一个方向的波形记录作相关计算时,垂直向结果对于重复地震识别可信度最高(李宇彤等,2008;马晓静等,2017)。本文选取垂直向波形资料,考虑到不同仪器记录平坦频带范围的差异及环境噪声的影响,将地震波形转换为SAC格式,进行去倾斜及去趋势处理,分别对各研究区信噪比较高的地震事件进行频率分析,选用0.5—10 Hz带通滤波器进行波形预处理较为合适。为提高计算精度,以事件发震时刻为时间零点,Pg波到时前1 s开始截取,选择4倍Sg、Pg震相走时差长度的波形进行互相关分析(董非非等,2016;马晓静等,2017;汪建等,2018),该窗长基本包含P波、S波及尾波波列,同时避免后续噪声记录影响互相关计算结果。
2.2 计算结果由于距离荣昌—隆昌区、綦江区最近的台站荣昌台和万盛台位于震群中,为避免台站位置对波形互相关计算结果的影响,2个台站数据未参与互相关分析,而其他台站距离较远,故2个区域只做2台波形互相关分析。表 1给出5个研究区地震事件分别进行互相关计算的结果,其中识别得到:同时被2个台站记录且各台cc≥0.8的地震对(简称2台相关重复地震对)有358对,涉及342个地震事件,约占地震总数的27%,且cc≥0.9的2台相关重复地震对有115对;同时被3个台站记录且各台cc≥0.8的地震对(简称3台相关重复地震对)有122对,cc≥0.9的3台互相关重复地震对有58对;若多个地震之间两两相关,则称为多重地震对,共识别出3重及以上地震对74组;在荣昌—隆昌区、綦江区识别出的重复地震所占比例低于20%,武隆区所占比例最高,为36.05%,巫山—巴东区识别出的重复地震所占比例为35.4%,与汪建等(2018)计算的巫山地区重复地震比例33%相接近。
| 表 1 重庆地区利用波形互相关识别的“重复地震”结果统计 Table 1 Statistics of repeating earthquakes recognized by waveform cross-correlation in the Chongqing area |
表 2列出荣昌—隆昌区识别出的9重地震对参数,其中:该组重复地震组间震级最大差值为ML 1.3,最小为ML 0.0;深度最大差值为4 km,最小为0 km;组间距(组间最大距离)为6.36 km。对重复地震发震时间间隔进行统计,发现重复周期具有明显变化,时间跨度从几十天到几百天不等,最大重复间隔接近3年。
| 表 2 荣昌—隆昌区识别出的9重地震对 Table 2 A nonuple recognition in the Rongchang-Longchang area |
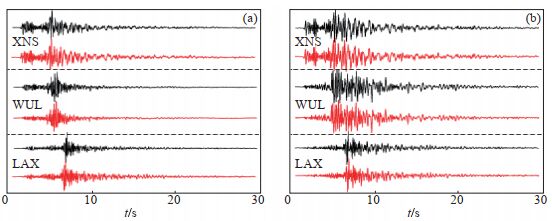
以2011年8月4日6时1分和2013年2月5日14时42分发生在武隆区的2个地震为例,其中震级分别为ML1.7和ML1.8,重复间隔为552天,给出仙女山(XNS)、武隆(WUL)、朗溪(LAX)3个台站的垂直分量原始波形,波形自P波到时前1 s截取,波形长度30 s,经预处理和滤波,给出滤波后波形,结果见图 2,由式(1)计算可得,3个台站的互相关系数为0.983、0.979、0.985,波形相似度较高,说明随着时间的推移,该组地震对传播路径上的地下介质相对稳定。
|
图 2 2个地震在XNS、WUL、LAX地震台垂直分量原始及滤波后波形 (a)原始波形;(b)滤波后波形 Fig.2 Original and filtered waveforms of the vertical component of two earthquakes recorded at the XNS, WUL and LAX stations |
精确的地震定位是地震学研究的一项基础工作,各种地震学研究(地震活动性分析、三维速度结构模型反演等)依赖于地震观测报告产出数据,其中震源位置多采用传统迭代反演方法和一维地壳结构速度模型来获得。由于参与地震定位的台站数量、分布不同以及震相拾取误差的存在,导致地震观测报告中的定位精度必然存在差异。因此,对产出的大量地震观测报告中地震定位精度进行科学且合理的评估就显得尤为重要(马晓静等,2017)。
Geller等(1980)研究认为,重复地震水平间距小于优势震相频率波长1/4。Schaff等(2004)对中国大陆及邻区具有3个或以上台站Lg波记录的重复地震的重新相对定位结果显示,重复地震对间距确实在1 km范围内。据此,文中假定重复地震间距小于1 km,且由地震台网测得的重复地震表观距离系台网定位误差所致,重复地震在同一台站记录的同一震相走时差即为观测报告中震相的拾取误差(蒋长胜等,2008)。
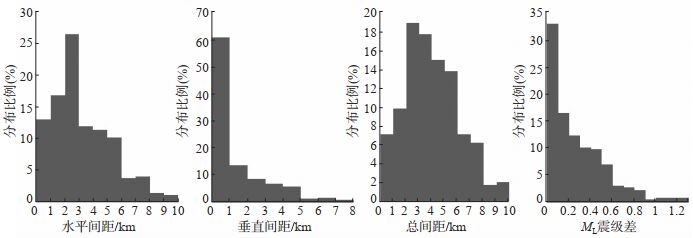
对得到的358个重复地震对,就水平间距、垂直间距、总间距和震级差分布比例进行统计分析,结果见图 3。由图 3可见,重复地震对之间的震级差在ML 1.3以内,平均震级差为ML 0.3,根据地震观测报告中的定位结果,按水平间距划分,重复事件对80%分布在5 km内,90%分布在6 km内;按垂直间距划分,分布75%在2 km内,85%分布在3 km内;按总间距划分,70%分布在5 km内。若以累计分布80%的参数值作为特征指标,重庆数字地震台网的垂直定位误差约为3 km,水平定位误差约为5 km。
|
图 3 重复地震对水平间距、垂直间距、总间距及震级差的比例分布 Fig.3 Proportional distribution of the horizontal spacing, vertical spacing, total spacing, and magnitude difference of the repeating earthquakes |
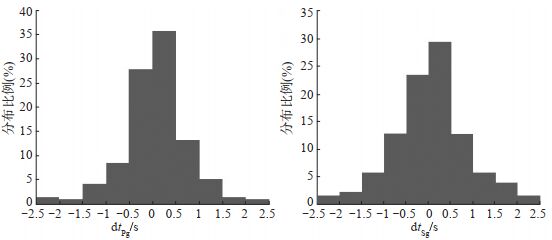
根据地震观测报告中的Pg、Sg震相到时,剔除权重为0的震相数据,将重复地震对的震相走时差做柱状统计图,结果见图 4。由图 4可见,Pg、Sg震相走时差约82%分布在-1—1 s范围内,约63%分布在-0.5—0.5 s范围内,其中Pg、Sg震相走时差绝对值均值分别为0.52 s和0.68 s。若以走时差绝对值均值为指标,取一位小数,则重庆数字地震台网的Pg、Sg震相拾取误差分别为0.5 s和0.7 s。因所选地震震源深度主要集中在4—7 km范围内,根据三峡水库库首区最小一维速度模型(赵旭等,2007)中震源深度4—6 km对应Pg波速度5.40 km/s,Sg波速度3.00 km/s,以及重复地震对间距在1 km内的理论和经验,Pg、Sg震相走时差应在理论所限的0.19 s和0.33 s以内。可见,重庆数字地震台网观测报告中给出的Pg、Sg震相拾取精度和理论值存在一定差距,人工震相拾取尚有较大提升空间。
|
图 4 重复地震对的Pg、Sg走时差分布 Fig.4 Distribution of the travel-time difference of Pg and Sg phases of the repeating earthquakes |
对5个研究区“重复地震”相关参数进行统计,结果见表 3,可见:武隆区重复地震之间垂直间距平均值在1 km以内,水平间距平均值在2 km以内,Pg、Sg震相走时差平均值在0.4 s以内,该区垂直、水平间距和走时差平均值最低,表明该区地震定位精度和震相拾取精度最高,可能是因为靠近该区的彭水电站6个企业台参与了地震定位,明显提高了该区的地震监测能力;荣昌—隆昌区重复地震之间垂直和水平间距平均值在3 km以内,Pg、Sg震相走时差平均值在0.5 s以内,虽然该区附近本地台站较少,但其西侧的四川数字地震台网泸州、花马寺、汉王山等台站能够参与地震定位,增强了该区地震监测能力;巫山—巴东区和石柱区重复地震之间水平间距平均值在5 km以内,2个研究区的水平定位误差均在重庆地区水平间距的优势分布范围内,巫山—巴东区Sg震相走时差平均值接近0.9 s,差值较大,是因为该区大部分地震位于湖北省巴东县境内,人工拾取本地台站记录的Sg震相误差较大;綦江区重复地震之间水平间距平均值在6 km以上,Pg、Sg震相走时差平均值在0.8 s以上,由图 1可知,该区周边台站分布较为稀疏,且无外省台站参与地震定位,因此,适当增加该区域地震台站数量并合理布局,将有效提高重庆地区地震定位精度。
| 表 3 5个研究区重复地震参数统计 Table 3 Statistics of parameters of repeating earthquakes for five research areas |
对重庆地区1 251次地震波形进行互相关计算,识别出同时被2个台站记录且各台cc≥0.8的地震对358对,3重及以上重复地震74组,涉及342个地震事件,约占地震总数的27%。假定重复地震对间距小于1 km,地震台网测得的2个地震间距离系台网定位误差所致,而相应的震相走时差为人工拾取误差,将358对重复地震对用于定量判断地震目录中震相拾取误差和评估台网定位精度,结果显示:重庆数字地震台网的垂直定位误差约为3 km,水平定位误差约为5 km,Pg、Sg震相拾取误差分别为0.5 s和0.7 s。重庆数字地震台网的水平定位误差和震相拾取误差较广东地区(马晓静等,2017)结果有一定差距,水平定位误差与首都圈地区(蒋长胜等,2008)、江西地区(董非非等,2016)结果接近。对5个研究区分别进行震相拾取误差和台网定位精度评估,结果显示:武隆区震相拾取和地震定位精度最高;綦江区最低,观测条件有待改善。
本研究采用的波形互相关程序由江西省地震局查小惠工程师提供,重复地震辅助计算程序由江西省地震局董非非工程师提供,在此表示感谢。
陈凯, 孙国栋, 易江, 等. 2019. 重庆及邻区地震精定位及活动性分析[J]. 地震地磁观测与研究, 40(5): 8-20. |
董非非, 邓辉, 郑斌, 等. 2016. "重复地震"在江西省及邻区测震台网定位精度评价中的应用[J]. 华北地震科学, 34(2): 73-78. DOI:10.3969/j.issn.1003-1375.2016.02.013 |
蒋长胜, 吴忠良. 2005. 由"重复地震"给出的中国地震台网的定位精度估计[J]. 中国地震, 21(2): 147-154. DOI:10.3969/j.issn.1001-4683.2005.02.002 |
蒋长胜, 吴忠良, 李宇彤. 2008. 首都圈地区"重复地震"及其在区域地震台网定位精度评价中的应用[J]. 地球物理学报, 51(3): 817-827. DOI:10.3321/j.issn:0001-5733.2008.03.022 |
李宇彤, 吴忠良, 蒋长胜, 等. 2008. 利用辽宁区域地震台网记录分析"重复地震"[J]. 地震学报, 30(4): 383-396. DOI:10.3321/j.issn:0253-3782.2008.04.006 |
李宇彤, 蒋长胜. 2011. 波形相关意义"重复地震"研究综述[J]. 中国地震, 27(4): 335-347. DOI:10.3969/j.issn.1001-4683.2011.04.001 |
马晓静, 吕作勇. 2017. 广东地区重复地震识别及其在台网定位评价中的应用[J]. 华南地震, 37(1): 22-28. |
孟真, 宋晓东. 2019. 龙门山断裂带周缘重复地震识别及其在台网定位评价中的应用[J]. 地震, 39(3): 166-177. DOI:10.3969/j.issn.1000-3274.2019.03.015 |
汪建, 王同军, 杨亚运, 等. 2018. 利用重复地震观测重庆巫山地区地壳介质变化[J]. 地震地磁观测与研究, 39(6): 16-22. DOI:10.3969/j.issn.1003-3246.2018.06.003 |
王同军, 陈凯, 舒涛, 等. 2016. 重庆三峡测震台网子台站地噪声及监测能力分析[J]. 内陆地震, 30(1): 49-55. |
王小龙. 2007. 三峡重庆库区数字遥测台网地震监测能力评估[J]. 四川地震, 11061106(3): 43-45. DOI:10.3969/j.issn.1001-8115.2007.03.009 |
赵旭, 李强, 蔡晋安. 2007. 三峡库首区最小一维速度模型研究[J]. 大地测量与地球动力学, 27(Z1): 1-7. |
Geller R J, Mueller C S. 1980. Four similar earthquakes in central California[J]. Geophys Res Lett, 7(10): 821-824. DOI:10.1029/GL007i010p00821 |
Rubin A M. 2002. Using repeating earthquakes to correct high-precision earthquake catalogs for time-dependent station delays[J]. Bull Seismol Soc Am, 92(5): 1647-1659. DOI:10.1785/0120010180 |
Schaff D P, Richards P G. 2004. Repeating seismic events in China[J]. Science, 303(5661): 1176-1178. DOI:10.1126/science.1093422 |
 2020, Vol. 41
2020, Vol. 41

