2. 中国北京 102628 北京港震科技股份有限公司
2. Beijing Geolight Technology Corporation Limited, Beijing 102628, China
地震计传感参数包括地震计各分向传感器的灵敏度、敏感轴方向角(敏感轴在水平面坐标系的投影与X轴的夹角)和敏感轴倾角(敏感轴与其在水平面的投影之间的夹角)。通常,地震计外壳上有一指向标志,生产过程中内部各分量传感器的调试均以此为基准进行。在地震计使用过程中,需保证地震计水平,且指向标志与地理方向一致,则仪器记录即为所在位置振动信号的UD、EW、NS分量。显然,地震计3个传感器的敏感轴方向应以水平面指向为基准且完全正交。但是,在地震计实际生产过程中,受机械加工和人为操作误差的影响,传感器实际敏感方向与定义之间存在一定误差,地震计灵敏度也由于多方面原因与标称值存在一定误差。按中华人民共和国地震行业标准DB/T 22—2007(中国地震局,2007)规定,多数地震计生产厂家以2 000 V·s/m为地震计的标称灵敏度,允许误差为±60 V·s/m,安装角度误差未直接提及,但规定地震计横向灵敏度小于1%。实际测试表明,在振动台上旋转地震计,总可以找到最小横向灵敏度方向,此时横向灵敏度小于0.01%。把该最小横向灵敏度方向作为地震计敏感方向,在地震计测试中出现的横向即由安装角度误差引起,因此,标准DB/T 22—2007实际规定了安装角度的误差范围。
显然,地震计传感参数对地震观测具有重要作用,是确保地震观测资料质量的关键。使用振动台可以直接、客观地测定上述地震计传感参数。但是,在许多场合没有振动台,而且,大量振动台测试耗时较长,测试工作效率不高。本文提出采用对比法成批测试地震计传感参数,在没有振动台的情况下,可以一次测试多台地震计传感参数,拓展地震计参数的测试场合,在大批量测试时,还可以快速完成大量地震计传感参数测试,提高测试效率。
对比法测试法在地震计测试中应用广泛(Holcomb et al,1990, 2005;Pavlis et al,1994;吕永清等,2007;Niu et al,2011;Tasič et al, 2013;Zha et al,2013;林湛等,2013;李少睿等, 2014, 2016;谢剑波,2014;黄静等,2015;陈继锋等,2016;龙剑锋等,2016;张正伟等,2016),一般用于灵敏度测试、井下地震计安装方位角测试等。本文将对比测试法拓展应用到传感参数测试,与已有测试方法相比有较大发展。已有方法多基于频谱比、功率谱比方法测试灵敏度,使用旋转、相干函数方法测定方位角,而非全面测试地震计传感参数。本文提出采用标准地震计记录数据获得测试场地地面振动UD、EW、NS分量信号,通过投影关系,采用非线性问题最优化拟合方法,同时确定传感器的传感参数,并给出测试精度评价方法,有助于直接了解、控制测试质量。
1 测试方法与算法 1.1 真实地面振动获得算法开展对比法测试需要一台标准地震计,本研究使用一台GL-CS60地震计作为标准地震计,该地震计由北京港震科技股份有限公司生产,经振动台精确测试XYZ和UVW模式输出时的传感参数,并确认无误。
地震观测时需要地震计记录所在位置地理坐标3个轴向的振动分量,即UD(垂直向)、EW(东西向)、NS(北南向),组成地震计的观测坐标系。此外,地震计自身具有一个仪器坐标系,为三轴正交坐标系,与观测坐标系相同,包括2个相互垂直的水平轴和一个与水平面垂直的垂直轴,每个轴的正向对应一个传感器的敏感方向。这样的仪器坐标系称为XYZ坐标系。开展地震观测时,使地震计Y轴正向指向正北(通常地震计提供准确指向参考标志和对准方法),此时XYZ坐标系与大地坐标系重合,观测记录所得即为测点大地坐标系下的振动。
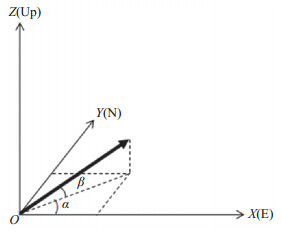
在观测过程中,测点的振动信号由地震计的3个正交传感器转换为3路电信号,经数据采集记录器转换为数字信息记录,与地震观测系统参数共同处理,获得所在测点的振动记录信号。如图 1所示,各路传感器的记录信号与地面振动成正比,比例系数即为灵敏度s。定义传感器敏感方向正向在水平面的投影与X轴的夹角为α,称为方向角,传感器敏感方向正向与其水平面投影之间的夹角为β,称为倾角,则传感器输出电压公式为
| $ u = s\left({{v_x}\cos \alpha \cos \beta + {v_y}\sin \alpha \cos \beta + {v_z}\sin \beta } \right) + sn $ | (1) |
|
图 1 仪器坐标系下传感夹角定义 Fig.1 Sensing angle definition in instrumental coordinates |
式中,u为输出电压,s为传感器速度灵敏度,vx、vy、vz分别为X、Y、Z方向的真实地面振动速度分量,n为仪器自噪声。
一台三分向地震计装有3个传感器,把3个传感器的输出方程组合起来,考虑到仪器自噪声的存在,以矩阵形式写成
| $ \left[ {\begin{array}{*{20}{l}} {{u_1}}\\ {{u_2}}\\ {{u_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{s_1}}&0&0\\ 0&{{s_2}}&0\\ 0&0&{{s_3}} \end{array}} \right]\left\{ {\left[ {\begin{array}{*{20}{l}} {\cos {\alpha _1}\cos {\beta _1}}&{\sin {\alpha _1}\cos {\beta _1}}&{\sin {\beta _1}}\\ {\cos {\alpha _2}\cos {\beta _2}}&{\sin {\alpha _2}\cos {\beta _2}}&{\sin {\beta _2}}\\ {\cos {\alpha _3}\cos {\beta _3}}&{\sin {\alpha _3}\cos {\beta _3}}&{\sin {\beta _3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{n_1}}\\ {{n_2}}\\ {{n_3}} \end{array}} \right]} \right\} $ | (2) |
按矩阵符号表示为
| $ U = S\left({P{V_{xyz}} + N} \right) $ | (3) |
式中,U为记录电压向量,S为灵敏度矩阵,P为投影矩阵,Vxyz为XYZ坐标速度向量,N噪声向量,分别为
| $ U = \left[ {\begin{array}{*{20}{l}} {{u_1}}\\ {{u_2}}\\ {{u_3}} \end{array}} \right]\;\;\;\;\;S = \left[ {\begin{array}{*{20}{l}} {{s_1}}&0&0\\ 0&{{s_2}}&0\\ 0&0&{{s_3}} \end{array}} \right]\;\;\;\;{V_{xyz}} = \left[ {\begin{array}{*{20}{l}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right] $ |
| $ P = \left[ {\begin{array}{*{20}{l}} {\cos {\alpha _1}\cos {\beta _1}}&{\sin {\alpha _1}\cos {\beta _1}}&{\sin {\beta _1}}\\ {\cos {\alpha _2}\cos {\beta _2}}&{\sin {\alpha _2}\cos {\beta _2}}&{\sin {\beta _2}}\\ {\cos {\alpha _3}\cos {\beta _3}}&{\sin {\alpha _3}\cos {\beta _3}}&{\sin {\beta _3}} \end{array}} \right]\;\;\;\;\;N = \left[ {\begin{array}{*{20}{l}} {{n_1}}\\ {{n_2}}\\ {{n_3}} \end{array}} \right] $ |
只要3个传感器中任意2个的敏感方向不平行,矩阵P的秩就是3,由式(3)可得
| $ {V_{xyz}} = {P^{ - 1}}{S^{ - 1}}U - {P^{ - 1}}N $ | (4) |
由式(4)计算真实的地面振动速度受仪器自噪声的影响。由于仪器自噪声是不确定的,要精确求解式(4)是不可能的。若选择合适的信号频带,使信噪比足够大,可忽略噪声影响,则式(4)可简化为
| $ {V_{xyz}} = {P^{ - 1}}{S^{ - 1}}U $ | (5) |
这样,使用标准地震计记录与已知3个传感器参数,选择信噪比足够大的频带,由式(5)计算Vxyz,即可得仪器位置的振动速度向量。
1.2 信噪比估计与测试频带选择自噪声是指所测2台以上地震计波形记录之间不相干的部分,相干部分认为是地动信号。信噪比是信号有效值与噪声有效值的比,不可能直接由记录获得。
在对比法测试中,采用性能相近的2台地震计,使用P Welch方法计算波形功率谱密度Pii、Pjj及互功率谱密度Pij,计算2台地震计记录信号的相干系数,公式如下
| $ {\gamma ^2} = \frac{{{{\left| {{P_{ij}}} \right|}^2}}}{{{P_{ii}}{P_{ij}}}} $ | (6) |
假设2台仪器的信噪比水平一致,则可由下式计算地震计信噪比(Holcomb,1990)
| $ {\rho ^2} = \frac{X}{N} = \frac{\gamma }{{1 - \gamma }} $ | (7) |
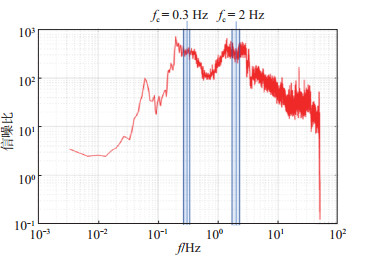
式中,ρ为信噪比,X为信号的功率谱密度,N为噪声功率谱密度,γ为2路信号的相干系数。由式(7)可知,信噪比越大,相干系数越大,则式(5)中Vxyz近似越接近精确值,计算得到的地震计传感参数就越准确。如,相干系数γ = 0.999 9,计算得到信噪比约99.995倍,约等于100倍。参与测试的2台地震计记录的信噪比曲线见图 2,可见:在频点2 Hz附近频带内,地震计信噪比最高,平均可达约400倍;在低频部分的0.3 Hz附近频带内,地震计信噪比平均约350倍。因此,2个频段是传感参数测试较理想的选择。
|
图 2 对比法测试中信噪比随频率变化与频带选择 Fig.2 Selection of frequency band with ratio on signal to noise curve in side by side comparison computation |
采用以中心频率为基准的倍频程来定义频带宽度。频带越窄,计算所得传感参数更接近于中心频率单频的传感参数值。在实际计算中,采用1/3倍频程的频带宽度,给定中心频率fc,则频带范围为0.890 9 fc—1.122 5fc。如图 2所示,试验中分别选用0.3 Hz、2 Hz作为计算中心频率。
1.3 XYZ传感参数对比计算方法实际应用中,地震计具有相互正交的一个垂直轴、2个水平轴共3个分向,对应或等效传感器的3通道输出。将标准地震计记录代入式(5),计算得到给定测试场地振动速度向量Vxyz,获得一个单分向地震传感器输出波形信号记录的N样点时间序列ui(i = 1,2,...,N)后,对于任意一组传感参数(s′,α′,β′),代入式(1),计算可得传感器输出时间序列
| $ f\left({s', \alpha ', \beta '} \right) = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^n {{{\left[ {{u_i} - {u_i}^\prime } \right]}^2}} } $ | (8) |
求解该问题就是求得一组参数(s′,α′,β′),使得f (s′,α′,β′)最小,作为问题的解。这是一个非线性问题,本文采用无约束、非线性最优化方法求解。
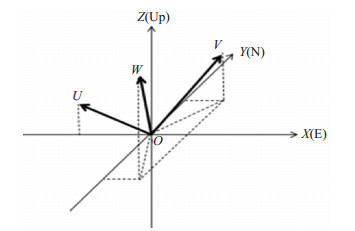
1.4 UVW传感参数对比计算方法在地震计设计方案中,3个相同传感器斜挂方式安装已被广泛使用。标称的3个传感器的敏感轴向正交,其水平面投影成120°夹角均匀分布,并与水平面投影成35.264 4°夹角(图 3),这类仪器的直接输出为UVW输出信号。在地震计内,通过电路把UVW输出信号变成与传统地震计一致的XYZ输出信号。与传统地震计相同,斜轴轴向间的夹角和灵敏度也存在误差,精确确定UVW 传感器的传感参数,对于了解、控制地震计最终输出信号的传感参数误差,追溯误差来源具有重要意义。
|
图 3 斜挂式地震计传感方向及投影角度 Fig.3 Sensing angles and their projection on horizontal plane of an inclined suspension seismometer |
用标准地震计记录按(5)式计算得到测试场地地面振动XYZ向量Vxyz,按式(9)计算测试场地振动UVW速度向量Vuvw = [Vu,Vv,Vw]
| $ \left[ {\begin{array}{*{20}{l}} {{V_u}}\\ {{V_v}}\\ {{V_w}} \end{array}} \right] = \frac{1}{{\sqrt 6 }}\left[ {\begin{array}{*{20}{c}} { - 2}&0&{\sqrt 2 }\\ 1&{\sqrt 3 }&{\sqrt 2 }\\ 1&{ - \sqrt 3 }&{\sqrt 2 } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{v_x}}\\ {{v_y}}\\ {{v_z}} \end{array}} \right] $ | (9) |
以矩阵形式表示为
| $ {V_{uvw}} = T{V_{xyz}} $ | (10) |
式中,T为变换矩阵。这样,在获得Vxyz后,可由式(10)计算Vuvw。简化式(10),可得
| $ {V_{xyz}} = {T^{ - 1}}{V_{uvm}} $ | (11) |
将式(11)带入式(3),得
| $ U = SP{T^{ - 1}}{V_{uvw}} + SN $ | (12) |
测试中选择信噪比足够大的频段,忽略噪声,采用式(10)计算得到Vuvw,给定一组传感参数,忽略噪声,即可通过式(12)计算得到传感器输出。为便于计算,将式(12)展开,得
| $ \begin{array}{l} u = \frac{s}{{\sqrt 6 }}\left[ {{V_u}(- 2\cos \alpha \sin \beta + \sqrt 2 \cos \beta) + {V_v}(\cos \alpha \sin \beta + \sqrt 3 \sin \alpha \sin \beta + \sqrt 2 \cos \beta) + } \right.\\ \;\;\;\;\;\;\;\;\left. {{V_w}(\cos \alpha \sin \beta - \sqrt 3 \sin \alpha \sin \beta + \sqrt 2 \cos \beta)} \right] \end{array} $ | (13) |
这样,可按照上述传感器参数求解办法,获得斜轴地震计传感器参数。需要说明的是,在斜轴传感器描述中,使用悬挂角的概念,与本文定义的倾角为互补关系,可在程序中直接把斜轴传感器的倾角变换为悬挂角。
2 对比法测试与数据处理流程(1)测试数据获得。测试时,把待测地震计和标准地震计安装在同一坚实平台上,方向指向一致,调平上电后由仪器自动完成调零。一次测试多台地震计时,需要使用2台以上数据采集器,此时所有数据采集器需连接GPS,并与GPS保持同步1小时以上。数据采集器通道采集参数设置需一致,并经精确校准。采集参数设置如下:采样率100 sps,最小相位,输入电压满幅值±2.5 V,连续记录1小时以上。
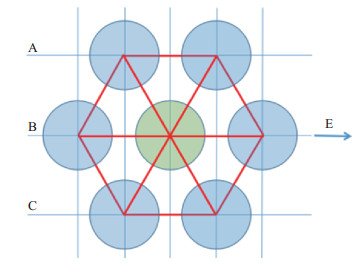
(2)测试地震计布局。如图 4所示,6台地震计同时参与测试,采用正六边形布局,每个顶点放一台地震计,中心放置标准地震计,定向平行指向同一方向。这样,待测地震计与标准地震计的中心距相同,指向一致。
|
图 4 同时测试的6台地震计布局 Fig.4 Distribution of 6 instruments measured at the same time |
(3)数据选择。通过波形浏览程序,选择、截取相对干扰较小的一小时记录波形数据。
(4)数据处理过程与误差估计。对选择得到的数据,按设置的频带范围滤波,选择一定长度的数据窗、1/2长度重叠,使用滑动窗口数据段计算求解地震计传感参数,得到多组地震计传感参数,取中值作为计算结果,计算标准差作为误差参考。
(5)结果判定。当计算得到的灵敏度误差小于0.2%,方位角误差小于0.1°(垂直向除外),倾角(悬挂角)误差小于0.1°,可认为满足地震计传感参数测量精度要求。
3 测试检验(1)测试仪器。本次试验采用北京港震仪器设备有限公司生产的EDAS-24GN地震计数据采集器及10台GL-CS60斜轴地震计。GL-CS60可以在UVW输出状态或XYZ输出状态进行工作,在XYZ输出模式下,GL-CS60输出与传统地震计一致。
(2)合成数据测试检验。将EDAS-24GN数据采集器记录的GL-CS60斜轴宽频带地震计数据作为标准记录,假设其对应的灵敏度、安装方位角、悬挂角均为标准值。按灵敏度为2 000±60 V·sm-1、安装方位角和悬挂角在标准值±1.5°范围内随机设定,使用式(1)合成10组XYZ输出待测地震计记录,使用式(12)合成10组UVW输出待测地震计记录,使用本文方法求解待测地震计传感参数。在合成记录中加上有效值为记录幅度有效值1%的白噪声(相当于100倍信噪比),使用本文方法求解待测地震计参数。结果统计见表 1、表 2。
| 表 1 XYZ模式地震计传感器参数测试模拟数据检验偏差统计 Table 1 Statistics of sensing parameters error of seismometer in XYZ mode computeded with synthetic data |
| 表 2 UVW模式地震计传感器参数测试偏差统计 Table 2 Statistics of sensing parameter error of seismometer in UVW mode computed with synthetic data |
(3)振动台测试检验。选择2台地震计,在振动台上测试XYZ输出方式和UVW输出方式的传感参数,把其中一台作为标准地震计,用对比法2次测试另一台地震计传感参数,结果见表 3。由表 3可见,UVW输出时,与振动台测试结果相比,灵敏度差小于0.2%,方向角差小于0.3°,悬挂角误差小于0.02°。XYZ输出时,灵敏度偏差小于0.05%,方向角偏差达0.593 1°(垂直向由于夹角较小,方向角度变化较大,统计时排除在外),倾角误差小于0.05°。方向角偏差略大与多次安装方向对准误差有关。
| 表 3 对比法与振动台测试结果比较数据 Table 3 Comparison for data from measurements between shake table and side-by-side method |
(4)批量地震计测试检验。采用2台双通道EDAS-24GN地震数据采集器和10台GL-CS60地震计样机进行比对测试,其中:1台UVW输出和XYZ输出的传感参数由振动台精确测定,作为标准地震计;其余9台分3组分别进行2轮对比法测试,测定UVW和XYZ输出的传感参数。2轮测试结果标准差统计结果见表 4,可见,①XYZ输出时,两轮测试的灵敏度标准差最大为2.117 V·s·m-1,最大误差约为0.1%,方向角误差除垂直向外均小于0.3°,水平向倾角偏差小于0.04°,垂直向小于0.2°,而EW与NS的夹角变化最大标准差小于0.065°;②在UVW输出时,方向角误差最大为0.288°,悬挂角差值最大标准差为0.049 7°,而U与V及V与W传感夹角的标准差为0.090 8°。总体来看,方向角偏差略大,与多次安装方向对准误差有关,其他参数偏差相当小,可以满足地震计测试需要。
| 表 4 批量地震计传感参数实测参数标准差统计 Table 4 Statistics of standard deviation of sensing parameters of seismometer in batch measurement |
对比法测试与振动台测试均为客观测试,依赖测试场地的振动,与振动台测试的不同主要表现在:①当前,测试振动台的振动均采用激光干涉法,由于激光波长的高稳定性,测试结果可靠性较高。对比法采用标准地震计记录,需要确保地震计工作状态的稳定性和记录的可靠性;②振动台可给出较大振动,测试时信噪比高,而对比法使用环境噪声作为信号源,振动幅度较小,总体信噪比较低;③振动台可输出单向信号,一次进行一个方向振动的测试,单纯、直接,对比法一次完成所有参数测试,理论上没有问题;④振动台输出强度可控,可测试任意频点的响应参数,对比法使用的场地噪声不可改变,只能选择利用合适频带的信号。需要说明的是,只要选择合适的频带,如本研究选用的2次海洋噪声和城市环境噪声的中心频率为0.3 Hz、2 Hz的频带,具有足够的信噪比,测试精度相当高,可以满足测试要求。
通过合成数据、振动台及批量地震计重复测试,表明使用对比测试方法,可准确测试地震计的传感参数,其精度可满足测试需要。在测试过程中发现,有时2次测试得到的方向角偏差较大,可能是因为2次安装定向存在误差,说明对于地震计提供的精确定向装置,需采用正确安装方式进行安装使用。总之,使用本文提出的方法,认真仔细地操作,可以取得精确的测试结果。
对比法可以以一台标准地震计为中心,同时完成多台地震计测试,测试数据采集过程避免人为干预,效率较高。本文开展的对比法测试实验在城市办公条件下进行,若条件允许,选择夜间、干扰小的场地进行测试,测试效果将更好。
本文提出的测试方法只需要地震数据采集器和一台标准地震计,对测试设备要求较低,可在许多场合应用,完成地震计传感参数测试,可以完成工厂生产时的批量地震计传感参数测试,也适用于地震仪器不能移动的固定地震台站,在不影响其日常观测的情况下,进行地震计传感参数校准测试。
本文计算基于Matlab平台及信号处理工具包编程完成。
陈继锋, 李亮, 李少睿, 刘白云, 陈晓龙. 2016. 甘肃省测震台网地震台站地震计方位角检验与校正[J]. 地震工程学报, 38(3): 460-465. DOI:10.3969/j.issn.1000-0844.2016.03.018 |
黄静, 房立华, 王长在, 郭永霞. 2015. 采用P波分析法校正北京遥测地震台网地震计方位角[J]. 地震地磁观测与研究, 36(4): 47-53. |
李少睿, 赵建和, 王党席, 董平江. 2014. 全国测震台站仪器方位角普查校正[J]. 地震地磁观测与研究, 35(1/2): 224-230. |
李少睿, 毛国良, 王党席, 罗治国. 2016. 井下地震计方位角检测技术应用研究[J]. 地球物理学报, 59(1): 299-310. |
林湛, 薛兵, 朱小毅, 陈阳, 李江, 彭朝勇, 刘洋君. 2013. 地震计灵敏度的对比测量法[J]. 地震, 33(1): 22-28. |
龙剑锋, 张学应, 骆佳骥, 赵希磊. 2016. 偏振分析算法测定井下地震计方位角偏差[J]. 地震地磁观测与研究, 37(1): 86-90. |
吕永清, 蔡亚先, 程骏玲. 2007. 确定地震计安装方位的相干性分析法[J]. 大地测量与地球动力学, 27(4): 124-127. |
谢剑波. 2014. 地震记录的时间域反褶积、仿真及在地震计方位角相对测量中的应用[J]. 地球物理学报, 57(1): 167-178. |
张正伟, 杨洪刚. 2016. 西昌台网地震仪方位角校正[J]. 华南地震, 36(2): 96-100. |
中国地震局. DB/T 22-2007地震观测仪器进网技术要求——地震仪[S]. 2007.
|
Niu Fenglin, Li Juan. 2011. Component azimuths of the CEArray stations estimated from P-wave particle motion[J]. Earthquake Science, 24(1): 3-13. |
Holcomb L G. A numerical study of some potential sources of error in side-by-side seismometer evaluations[R]. Albuquerque, New Mexico: U.S. Geological Survey, 1990.
|
Holcomb L G. Experiments in seismometer azimuth determination by comparing the sensor signal outputs with the signal output of an oriented sensor[R]. Albuquerque, New Mexico: U.S. Geological Survey, 2002.
|
Pavlis G L, Vernon F L. 1994. Calibration of seismometers using ground noise[J]. Bull Seismol Soc Am, 84(4): 1243-1255. |
Tasič I, Runovc F. 2013. Determination of a seismometer's generator constant, azimuth, and orthogonality in three-dimensional space using a reference seismometer[J]. Journal of Seismology, 17(2): 807-817. DOI:10.1007/s10950-012-9355-y |
Zha Y, Webb S C, Menke W. 2013. Determining the orientations of ocean bottom seismometers using ambient noise correlation[J]. Geophysical Research Letters, 40(14): 3585-3590. DOI:10.1002/grl.50698 |
 2019, Vol. 40
2019, Vol. 40

