0 引言

灾难性地震往往在短时间内造成严重破坏, 对人类社会造成巨大的生命财产损失, 因此科学合理地进行地震死亡人数预测对于防震减灾工作具有重要的指导意义(吴新燕等, 2014; 张文路等, 2016)。

地震死亡人数受多个因子的共同影响, 且死亡人数与影响因子之间存在复杂的非线性关系, 利用传统的方法很难科学地对此进行解释。为了解决该问题, 何明哲等(2011)提出了基于地震损伤指数的地震人员死亡预测方法。周德红等(2017)选用BP神经网络建立地震死亡人数预测模型。张莹等(2017)采用多元非线性回归法建立了基于多因素的地震灾害人员死亡评估模型。虽然以上研究对于该问题的解决均有一定的效果, 但也存在着一些不足, 如神经网络收敛速度过慢, 易陷入局部最优, 而多元非线性回归法的主观性较强。

基于此, 本文提出PCA和PSO算法优化的支持向量机模型, 用于地震死亡人数预测。首先采用PCA分析法对地震死亡人数的7个影响因子中的6个进行降维处理, 同时对第7个发震时刻因子单独进行区间分类, 将提取的主成分作为模型的输入向量; 然后利用PSO算法训练支持向量机从而获得最优参数; 最终建立PCA-PSO-SVM模型, 运用该模型对测试样本进行预测, 同时对比分析包含和不包含发震时刻因子的2种情况下的模型预测效果, 以期为地震死亡人数预测提供参考。

1 基本原理 1.1 主成分分析法

主成分分析法是通过构造原变量的线性组合得到维数较少且互不相关的新变量(王岩等, 2017; 史才旺等, 2018)。

设(X₁, X₂, …, X_n)为总体X的n个样本, 每个样本对应m维变量, 则对应矩阵为

$ {\mathit{\boldsymbol{X}}_{\mathit{\boldsymbol{m}} \times \mathit{\boldsymbol{n}}}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \ldots &{{x_{1n}}}\\ {{x_{21}}}&{{x_{22}}}& \ldots &{{x_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{x_{m1}}}&{{x_{m2}}}& \cdots &{{x_{mn}}} \end{array}} \right] $

(1)

首先求出式(1)矩阵的协方差阵, 为了减少变量间由量纲差异引起的误差, 根据公式${\rho _{ij}} = {\mathop{\rm cov}} \left({{X_i}, {X_j}} \right)/\sqrt {{\sigma _{ii}}{\sigma _{jj}}} $将协方差阵化为相关系数阵。通过求解相关系数阵的特征值λ₁≥λ₂≥λ_m≥0, 得到特征值对应的正交单位化特征向量e₁, e₂, …, e_m。第i个主成分的贡献率为λ_i/P(i = 1, 2, 3, …, m); $P = \sum\limits_{i = 1}^m {{\lambda _i}} $, 前q个主成分的累计贡献率为$\sum\limits_{i = 1}^q {{\lambda _i}} /P$。当前q个主成分累计贡献率大于85%时, 用其代替初始的影响因素进行分析, 一般是满足要求的。

1.2 粒子群优化算法

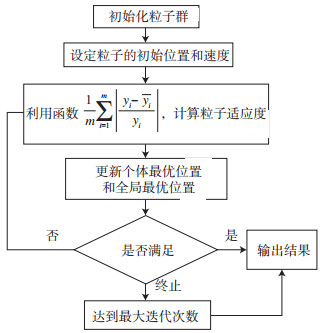
粒子群优化算法是通过模仿鸟群觅食而演化来的启发式优化算法, 它能够通过快速收敛来寻找全局最优参数(谢玮等, 2016), 具体流程见图 1。

1.3 支持向量机

支持向量机是由统计学理论发展而来的适用于小样本的机器学习方法, 其核心思想如下(文翔等, 2014; 王军, 2018)。

设训练样本集为(X_i, y_i), 其中, i=1, 2, …, n, X_i∈Rⁿ, 为输入矢量; y_i∈R, 为对应的输出结果, 则线性回归函数在高维特征空间的表达式为

$ {y_i} = \mathit{\boldsymbol{w}} \cdot \phi \left({{\mathit{\boldsymbol{X}}_\mathit{\boldsymbol{i}}}} \right) + b $

(2)

式中, $\phi \left({{\mathit{\boldsymbol{X}}_\mathit{\boldsymbol{i}}}} \right)$为样本数据转换到高维空间的非线性映射; w为权值矢量; b为偏置值。w、b有最优解, 可通过构造下列目标函数求得

$ \begin{array}{l} \mathop {\min }\limits_{w, b, \xi, {\xi ^*}} \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + C\sum\limits_{i = 1}^m {\left({{\xi _i} + \xi _i^*} \right)} \\ {\rm{ s}}{\rm{.t }}\left\{ {\begin{array}{*{20}{l}} {{y_i} - {\mathit{\boldsymbol{w}}^{\rm{T}}}\phi \left({{X_i}} \right) + b \le \varepsilon + \xi _i^*}\\ {{\mathit{\boldsymbol{w}}^{\rm{T}}}\phi \left({{X_i}} \right) + b - {y_i} \le \varepsilon + {\xi _i}}\\ {{\xi _i}, \xi _i^* \ge 0} \end{array}\quad \;\;(i = 1, \ldots, m)} \right. \end{array} $

(3)

式中, C为惩罚参数, 即对SVM分类出错时的惩罚程度, 此参数的设置有效防止了个别误差影响到支持向量机整体的优化性能。

利用最优化理论将式(3)复杂的二次规划问题转变为一种对偶问题

$ \begin{array}{l} L\left({\mathit{\boldsymbol{w}}, b, \xi, {\xi ^*}, a, {a^*}, r, {r^*}} \right) = \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + C\sum\limits_{i = 1}^m {\left({{\xi _i} + \xi _i^*} \right)} -\\ \sum\limits_{i = 1}^m {a_i^*} \left({{y_i} - {\mathit{\boldsymbol{w}}^{\rm{T}}} \cdot \phi \left({{X_i}} \right) - b - \varepsilon - \xi _i^*} \right) - \sum\limits_{i = 1}^m {{a_i}} \left({{\mathit{\boldsymbol{w}}^{\rm{T}}} \cdot \phi \left({{X_i}} \right) + b - {y_i} - \varepsilon - {\xi _i}} \right) - \sum\limits_{i = 1}^m {{r_i}} - \sum\limits_{i = 1}^m {r_i^*} \end{array} $

(4)

式中, $a_i^*、{a_i}$为位格朗日乘子; K(X_i·X_j)为支持向量机的核函数。常用核函数为RBF核函数, 其表达式为${K_g}\left({\left| {X - {X_i}} \right|} \right) = \exp \left({ - g{{\left| {X - {X_i}} \right|}^2}} \right)$。

求式(4)的最优解, 记为${\hat a^{(*)}} = {\left({{{\hat a}_1}, \hat a_1^{(*)}, \ldots, {{\hat a}_l}, \hat a_l^{(*)}} \right)^{\rm{T}}}$。选择$\hat a$的1个正分量$0 < {\hat a_j} < C/l$, 计算$\hat b = {y_i} - \sum\limits_{j = 1}^l {\left({\hat a_j^* - {{\hat a}_j}} \right)} K\left({{X_i} \cdot {X_j}} \right) + \varepsilon $, 或选择${{{\hat a}^{\rm{*}}}}$的1个正分量$0 < \hat a_j^* < C/l$, 计算$\hat b = {y_i} - \sum\limits_{j = 1}^l {\left({\hat a_j^* - {{\hat a}_j}} \right)} K\left({{X_i} \cdot {X_j}} \right) - \varepsilon $。

根据非线性回归问题在高维空间的解法, 最终得到支持向量机的回归函数为

$ f(X) = \sum\limits_{i = 1}^m {\left({a_i^* - {a_i}} \right)} \phi {\left({{X_i}} \right)^{\rm{T}}}\phi \left({{X_i}} \right) + b $

(5)

2 地震死亡人数预测

通过参阅前人文献(周德红等, 2017), 本文选取近50年来的32个样本地震数据, 其中, 前27个地震数据作为学习样本, 后5个地震数据作为测试样本, 原始数据见表 1。

地震发生的时间对灾难中人员伤亡数有较大影响。如果地震发生在白天, 那么会有较少的人员伤亡; 如果地震发生在晚上或者凌晨, 就会造成不可估量的人员伤亡。为了在预测中更准确地体现发震时刻对伤亡人数的影响, 本文将发震时刻分为2个时间段：发震时刻“1”表示白天(7:00—19:00), “0”表示夜晚(19:00—次日7:00);“ΔL”为震中烈度与抗震设防烈度之差。

2.1 主成分分析

由于发震时刻因子为离散变量, 而直接将PCA分析法用于离散变量是不适用的, 因此利用主成分分析法对其余6个影响因子进行降维处理, 相关系数矩阵见表 2, 归一化特征值, 各成分贡献率和累计贡献率见表 3。由表 3可见, 前3个主成分的累计贡献率为87.841%, 包含了原始变量绝大部分信息, 3个主成分表达式如下

$ Y_{1}=0.368 S_{1}+0.114 S_{2}+0.388 S_{3}+0.135 S_{4}+0.28 S_{5}-0.056 S_{6}\\Y_{2}=0.071 S_{1}+0.38 S_{2}-0.067 S_{3}+0.534 S_{4}-0.421 S_{5}-0.032 S_{6}\\Y_{3}=-0.064 S_{1}+0.443 S_{2}+0.014 S_{3}-0.161 S_{4}+0.121 S_{5}+0.794 S_{6} $

(6)

其中, S₁为震级, S₂为震源深度, S₃为震中烈度, S₄为抗震设防烈度, S₅为震中烈度与抗震设防烈度, S₆为人口密度。将3个新生成的线性无关的主成分替代原始地震死亡人数的6个影响因子, 并采用下式进行归一化处理

$ X_i^* = \left({{X_i} - {X_{\min }}} \right)/\left({{X_{\max }} - {X_{\min }}} \right) $

(7)

其中, X_i、$X_i^*$分别为各主成分的第i个样本数值与其相对应的归一化数值; ${{X_{\min }}}$、${{X_{\max }}}$分别为各个主成分的最小值、最大值。以归一化后的3个主成分数据作为输入变量来建立SVM模型, 归一化结果见表 4。

2.2 模型建立

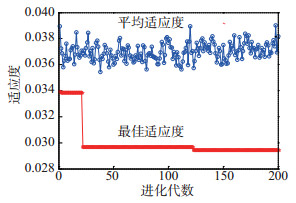
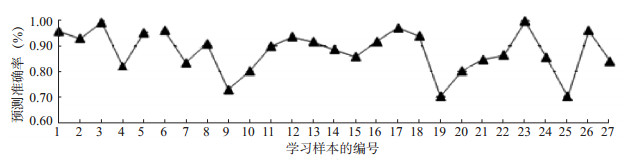
SVM核函数为径向基函数(RBF), 影响其性能的主要参数为核参数g和惩罚参数C。为搜索最佳SVM参数, 编写基于Matlab语言的粒子群优化支持向量机程序。以表 4中3个主成分作为输入变量, 地震死亡人数作为输出变量, 设置终止代数为100, 种群数量为20, 经反复训练获得粒子群算法最优适应度曲线(图 2), 同时搜索到SVM的最优参数C =16.128 8;g = 2.252 3;eps = 0.039, 并对学习样本进行预测准确率回判检验, 预测准确率回判结果见图 3。由图 3可见, 预测准确率回判结果最小误差2.9%, 最大误差30%, 平均误差11.99%, 因此该模型可用于测试样本的预测。

2.3 预测结果与分析

为研究发震时刻对模型预测精度的影响, 分别讨论输入向量包含和不包含发震时刻因子的2种情况下模型的预测效果, 同时采用降维后的主成分数据作为PCA-PSO-SVM模型的输入向量, 而PSO-SVM模型和SVM模型的学习样本则未经PCA降维处理, 3种模型同时对测试样本进行预测, 结果见表 5、表 6。

由表 5、表 6可见：①在不考虑发震时刻的情况下, SVM模型的最小、最大、平均误差分别为6.12%、20.00%、12.28%, PSO-SVM模型的分别为5.98%、20.00%, 12.08%;PCA-PSO-SVM模型的分别为0.85%、20.00%、10%。PCA-PSO-SVM模型预测结果平均误差相比PSO-SVM、SVM模型分别降低2.08%、2.28%;②在考虑发震时刻的情况下, SVM模型的最小、最大、平均误差分别为4.59%、20.00%、10.68%, PSO-SVM模型的分别为4.27%、20.00%、10.51%, PCA-PSO-SVM模型的分别为0.25%、20.00%、7.18%。PCA-PSO-SVM模型预测结果平均误差相比PSO-SVM、SVM模型分别降低3.34%、3.50%。

由此可见, 加入发震时刻因子后3种模型的平均误差明显降低, 其中, PCA-PSO-SVM模型由于进行了主成分降维处理和粒子群算法的优化, 明显提高了运行效率, 降低了模型的复杂度, 故提升了预测精度。

3 结论

(1) 地震死亡人数与影响因子间关系错综复杂, 本文通过主成分降维与粒子群算法优化的支持向量机有机结合, 建立了基于PCA-PSO-SVM的地震死亡人数预测模型, 同时考虑了包含和不包含发震时刻因子对模型预测效果的影响。结果表明, 加入发震时刻因子后3种模型的平均误差明显降低, 其中, PCA-PSO-SVM模型由于进行了主成分降维处理和粒子群算法的优化, 明显提高了运行效率, 降低了模型的复杂度, 进而提升了预测精度。

(2) 在保证模型预测精度的前提下, 利用主成分分析法对地震死亡人数的6个影响因子进行降维处理, 提取3个主成分, 有效降低了模型维度, 提高了预测效率。

(3) PSO粒子群算法具有较快的收敛速度, 寻优得到的最优支持向量机参数C=16.1288;g = 2.2523, 较明显地优化了支持向量机的性能。