0 引言

重庆市位于四川盆地东南缘长江与嘉陵江交汇处。该区域主要的构造表现形式为发育背斜高陡、向斜宽缓的一系列隔挡式褶皱, 地质构造复杂, 断裂较为发育, 且地表断裂构造形迹大多与褶皱构造伴生。该区毗邻中国南北地震带中段, 地处大陆岩石圈东西地壳差异较大的边缘过渡带内, 隶属一级构造单元——扬子准地台和秦岭地槽褶皱系, 二级构造单元为四川台坳、上扬子地台和北大巴山冒地槽(赵军龙等, 2007)。区内的地质构造按走向特征大致可分为3类：NE向的华蓥山断裂、七曜山—金佛山断裂、方斗山断裂、彭水断裂等, NW向的城口深断裂等, 以及NS向的长寿—遵义断裂等(赵军龙等, 2007)。从历史上中强地震的空间分布来看, 地震多发生在二、三级构造单元的边界断裂带附近及NE向背斜褶皱的轴部附近。2003年三峡水库开始蓄水, 重庆巫山—湖北巴东、石柱、奉节等地小震活动有所增加。为了探究地震活动与地质构造及人为活动之间的关系, 针对区域内的地质构造情况研究不同地震定位方法从而提高地震定位精度一直是地震学研究中的重要工作。贺曼秋等(2012)、魏红梅等(2015)对重庆荣昌及邻区的地震进行重定位, 发现地震活动与断裂构造展布形态密切相关。

中国地震局“十五”数字化地震观测网络项目建设完成后, 全国各数字地震台网日常资料分析处理中使用的是MSDP软件自带的单纯型、自适应法、HypSAT、LocSAT、Hypo2000等地震定位方法, 而重庆地震台网目前主要使用HypSAT、LocSAT定位方法来进行区域地震的定位和编目。但这2种方法对震中距较小区域内地震的定位深度并不准确。如何选取更适宜的定位方法及地壳速度结构模型以提高定位精度, 一直是地震监测人员努力的方向。本文利用2009年1月至2018年10月重庆数字地震台网及周边省局地震台网记录到的地震数据, 应用Hypo2000定位方法及双差定位方法进行重定位, 将重定位结果与中国地震台网中心地震目录进行比较, 分析不同定位方法的优劣及适用性, 进而探究该区地震活动的可能原因(殷伟伟等, 2018)。

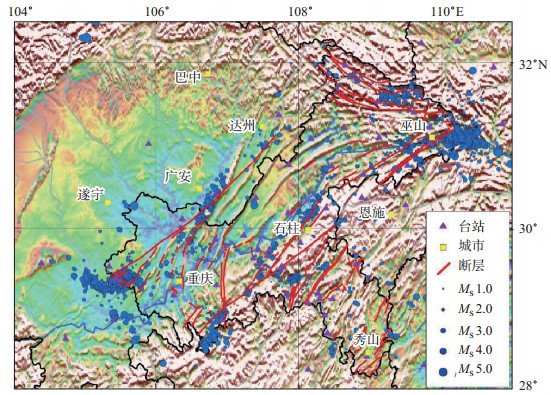
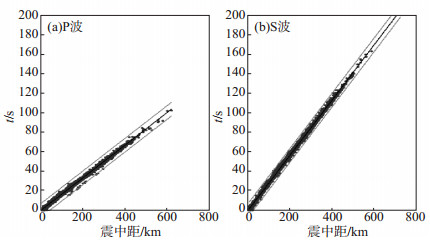
1 资料选取和研究方法 1.1 台站分布和数据提取

本文选取了重庆数字地震台网建成以来的观测资料, 震相数据来源于国家地震科学数据共享中心(http://earthquake.cn), 从中国地震台网中心地震目录中查询得到重庆台网的震相报告, 其中包含重庆及邻区(26°—35°N, 103°—113°E)2009年1月至2018年10月5 637个M_S＞0.5地震。所使用地震的震中及台站分布如图 1所示, 其中, 重庆数字地震台网固定台站36个, 流动台站4个, 周围邻近省份台站31个。为了避免人工拾取到时震相数据可能存在的误差, 对收集到的地震资料进行检查与筛选。根据震相报告提供的到时数据进行P波与震中距的时距曲线拟合, 对于少数偏差大于±5 s的震相数据, 在定位前予以剔除。筛选后的到时—震中距曲线如图 2所示, 由于拾取P波、S波到时的精度不同, 故反演过程中赋予P波震相权重为1.0, S波震相权重为0.8。

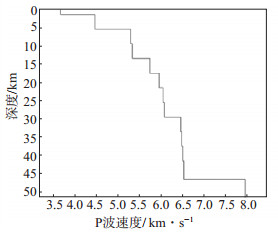
震相报告显示, 重庆地区地震的初步定位深度集中在10 km左右。重庆地区毗邻四川盆地的东南缘, 从西北向东南地形起伏呈现从低到高的走向, 区内多丘陵地貌, 七曜山—金佛山以南多山脉, 区域内地形起伏不大。速度结构特征差异不明显, 因此对数据进行定位分析时采用区域内单一速度结构模型。定位中选取了王小龙等(2010)根据接受函数得到的重庆地区一维速度结构模型(图 3), P波、S波波速比为1.7。

1.2 Hypo2000定位方法基本原理

Hypo2000方法是Klein(1978)在Geiger法基本思想上提出的一种绝对地震定位法。地震台站k观测到的震相到时T_k与理论到时t_k之差r_k可以表示为

$ r_{k}=T_{k}-t_{k} $

(1)

当r_k很小时, 对其作泰勒展开并忽略高次项可得

$ {r_k} = {\rm{d}}t + \frac{{\partial {t_k}}}{{\partial x}}{\rm{d}}x + \frac{{\partial {t_k}}}{{\partial y}}{\rm{d}}y + \frac{{\partial {t_k}}}{{\partial z}}{\rm{d}}z + {{\rm{e}}_k} $

(2)

在实际地震定位中, 地震一般会被多个台站记录到。当台站数大于未知数[式（2）中dx、dy、dz、dt]的个数时, 可使用最小二乘法求取未知数的解。令$\frac{{\partial {t_k}}}{{\partial x}} = {a_k}、\frac{{\partial {t_k}}}{{\partial y}} = {b_k}、\frac{{\partial {t_k}}}{{\partial z}} = {c_k}$, 如果有n个地震台站, 要使e_k取得最小值, 则必须满足

$ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{k = 1}^n {a_k^2} {\rm{d}}x + \sum\limits_{k = 1}^n {{a_k}} {b_k}{\rm{d}}y + \sum\limits_{k = 1}^n {{a_k}} {b_k}{\rm{d}}z + \sum\limits_{k = 1}^n {{a_k}} {\rm{d}}t = \sum\limits_{k = 1}^n {{a_k}} {r_k}}\\ {\sum\limits_{k = 1}^n {{a_k}} {b_k}{\rm{d}}x + \sum\limits_{k = 1}^n {b_k^2} {\rm{d}}y + \sum\limits_{k = 1}^n {{b_k}} {c_k}{\rm{d}}z + \sum\limits_{k = 1}^n {{b_k}} {\rm{d}}t = \sum\limits_{k = 1}^n {{b_k}} {r_k}}\\ {\sum\limits_{k = 1}^n {{a_k}} {b_k}{\rm{d}}x + \sum\limits_{k = 1}^n {{b_k}} {c_k}{\rm{d}}y + \sum\limits_{k = 1}^n {c_k^2} {\rm{d}}z + \sum\limits_{k = 1}^n {{c_k}} {\rm{d}}t = \sum\limits_{k = 1}^n {{c_k}} {r_k}}\\ {\sum\limits_{k = 1}^n {{a_k}} {\rm{d}}x + \sum\limits_{k = 1}^n {{b_k}} {\rm{d}}y + \sum\limits_{k = 1}^n {{c_k}} {\rm{d}}z + \sum\limits_{k = 1}^n {\rm{d}} t = \sum\limits_{k = 1}^n {{r_k}} } \end{array}} \right. $

(3)

利用式（3）可以求得震源参数的dx、dy、dz、dt解, 再根据初始震源位置(x₀, y₀, z₀)得到修正后的震源坐标(x₀ + dx, y₀ + dy, z₀ + dz), 即完成一轮迭代。然后, 将修正后的震源参数重新带入计算, 反复迭代修正, 直到震源参数的修正值小于给定的时间误差及位置误差时停止迭代, 最终得到定位后的震源位置及发震时刻。选取精确的速度模型对于获得准确的定位结果较重要, Hypo2000定位法充分考虑了地下速度结构的复杂性, 可以使用多重速度模型, 从而有效减少了速度模型差异所引起的走时误差。

1.3 双差定位方法基本原理

双差定位法是Waldhauser等（2000）提出的一种相对地震定位方法, 其基本原理如下（左可桢, 2018）。

震源i到台站j的体波观测到时T可以表述为如下积分形式

$ T_k^i = {\tau ^i} + \int_i^k u {\rm{d}}s $

(4)

其中, τⁱ为第i个震源的初始发震时刻; T_kⁱ为第i个震源到个台站的走时; u为慢度。使用截断的泰勒展开对其进行线性化, 即可得到地震波从地震i到台站k的观测到时与理论到时之差

$ r_k^i = \sum\limits_{l = 1}^3 {\frac{{\partial T_k^i}}{{\partial x_l^i}}} \Delta x_l^i + \Delta {\tau ^i} + \int_i^k \delta u{\rm{d}}s $

(5)

其中, $\Delta x_l^i(l = 1, 2, 3)$为震源位置参数在3个坐标轴方向上的扰动; $\Delta {\tau ^i}$为地震i的发震时刻扰动; δu为地震波的慢度扰动。因此, 地震i与地震j到达同一个观测台站k的走时残差之差为

$ r_k^i - r_k^j = \sum\limits_{l = 1}^3 {\frac{{\partial T_k^i}}{{\partial x_l^i}}} \Delta x_l^i + \Delta {\tau ^i} + \int_i^k \delta u{\rm{d}}s - \left({\sum\limits_{l = 1}^3 {\frac{{\partial T_k^i}}{{\partial x_l^j}}} \Delta x_l^j + \Delta {\tau ^j} + \int_i^k \delta u{\rm{d}}s} \right) $

(6)

其中, $r_k^i - r_k^j$即双差, 为2个地震事件的观测到时残差与计算到时残差之差, 也可以表述为如下形式

$ r_k^i - r_k^j = {\left({T_k^i - T_k^j} \right)^{{\rm{obs}}}} - {\left({T_k^i - T_k^j} \right)^{{\rm{cal}}}} $

(7)

观测到时残差${\left({T_k^i - T_k^j} \right)^{{\rm{obs}}}}$可以通过波形互相关技术或由绝对到时数据计算得到（段云歌等, 2013）。对所有台站(k =1, 2, …)和所有事件(i, j = 1, 2, …, N)得到的形如式（7）的方程构成1个线性系统, 以矩阵形式表述为

$ \mathit{\boldsymbol{WGm}} = \mathit{\boldsymbol{Wd}} $

(8)

式中, G为M×4N的偏微分矩阵, 其中, M为双差观测数, N为地震数; d为双差数据向量; m为待定震源参数改变量(∆xⁱ, ∆yⁱ, ∆zⁱ, ∆τⁱ)^T（i = 1, 2, …, N）的4N维向量; W为用于加权的对角矩阵。在反演过程中, 对所有地震重新定位后的震源参数增加了使其平均移动为0的约束条件, 公式如下

$ \sum\limits_{i = 1}^N \Delta {m_i} = 0 $

这是由于2个地震震中相距较近, 到同一个台站的射线路径在震源区之外基本上是重合的, 使用相对到时数据能够消除震源区外共同射线路径上由速度误差所造成的影响, 从而提高地震定位的精度。

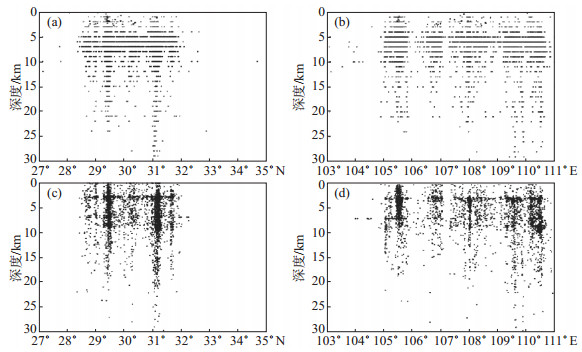
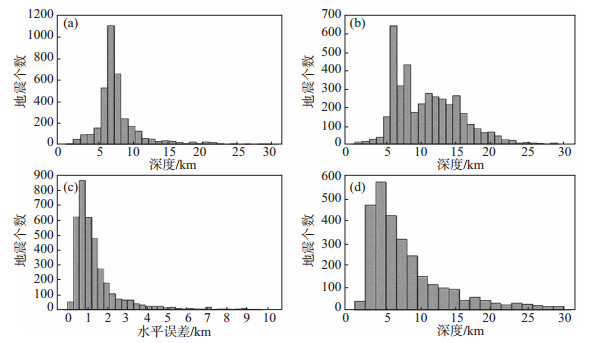
2 定位结果分析 2.1 Hypo2000定位分析

Hypo2000重定位后震中分布如图 4所示。由图 4可见, 与定位前相比, 重定位后沿平面方向震中位置有所收敛, 沿着断裂带展布形态分布。网内地震的震中与重定位前变化不大, 网外多个地震的震中位置发生了明显的变化, 说明Hypo2000定位方法对网外地震的定位精度值得探究（李兴泉等, 2018）。重定位前后震源深度分布如图 5（a）、5（b）所示。由图 5（a）、5（b）可见, 重定位后深度上震源位置表征出竖状分布, 与定位前的水平分层现象相比, 真实客观地反映了地下断层的分布情况。重定位前震源深度主要分布在7 km附近, 7 km是分析软件预设的缺省深度, 对于很多地震的实际情况并不合适。重定位后深度除了在7 km附近分布, 在10—16 km之间的地震个数也明显增多, 这与地震波形中的震相数据较一致。

重定位后水平、垂直误差分布如图 5（c）、5（d）所示。由图 5（c）、5（d）可见, 重定位后水平误差主要分布在0—2 km的范围内, 此类地震约占地震总数的86%;重定位后垂直误差略大于水平误差, 主要分布在0—5 km的范围内, 此类约占总数的82%。

2.2 双差法定位分析

利用经Hypo2000重定位后2009年1月至2018年10月的数据, 并舍弃走时残差大于1 s的地震事件, 选择震相数据大于4个的地震事件进行双差定位。设置地震对之间的最大距离为20 km, 共得到3 597个地震的31 562条P波绝对到时数据、38 548条S波绝对到时数据, 以及881 923条相对到时数据, 其中, P波相对到时数据373 096条, S波相对到时数据438 717条。速度模型选取研究区域的平均速度模型。因双差定位法需要形成地震对, 并且会反复调整地震对与地震簇中心的位置来获得最终的定位结果, 这会造成一些偏离地震簇中心的地震在计算中被丢弃, 进而造成参与实际定位的地震数量相对于地震目录会有所减少, 但这对地震序列空间分布的影响并不大, 并且对于揭示区域地震活动性具有一定的实践意义（赵博等, 2013）。

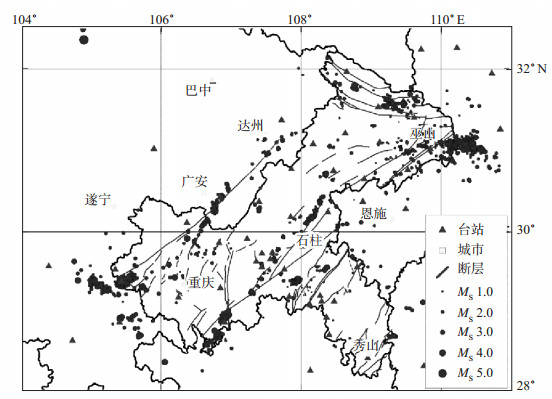
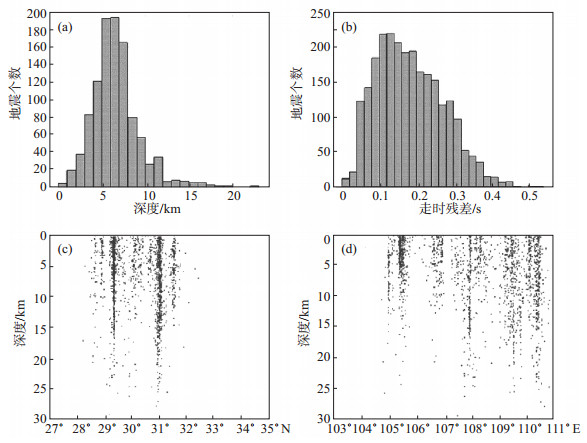
图 6为双差定位后的震中分布图。由图 6可见, 相比利用Hypo2000方法的定位结果, 双差定位后误差有了显著的降低。重定位后震中位置较Hypo2000方法定位后有所收敛, 向断裂带走向的分布有所聚集。图 7为双差定位后残差及深度分布图。由图 7可见, 深度为0—12 km的地震个数分布近似于正态分布, 与实际地震震相数据一致。重定位后的走时残差基本小于0.3 s, 此类地震个数占总数的92%。在深度上震源位置表征出竖状分布, 与Hypo2000方法定位结果对比可见, 在经度、纬度剖面有所收敛, 深度上的分层现象进一步消失。重庆及邻区地震主要发生在中上地壳内, 地震活动的下界面约在20 km附近, 震源较浅, 这与实际地质情况相一致（马宏生等, 2008）。

3 区域地震活动性分析

震源位置的研究对于探索地震孕育、发生的深部环境, 地震能量集结、释放的活动构造背景等具有重要意义。经过重定位的地震震源位置及深度、精度均会有所改善, 据此可以探究地震活动的成因。重定位后的结果显示, 重庆地区地震活动强度不高, 震源不深, 深度竖状分布主要集中在华蓥山基底断裂末端。历史上该区发生多次5级以上地震, 如1997年荣昌5.2级地震及其200多个余震, 其中, 深度最大达40 km, 在其分支——璧山断裂上也曾发生震源深度40 km左右的地震, 表明华蓥山基底断裂深度可达莫霍面顶部。另一个竖状分布集中区域为三峡库区, 主要在七曜山—金佛山基底断裂、高桥断裂、牛口断裂等附近, 七曜山—金佛山基底断裂长期以正断力学性质活动, 形成了重庆区域内最深的盖层中心, 厚度最大可达17 km。而湖北巴东附近的断裂同时会受到水库的影响, 这导致该区域浅层小震密集, 深部地震主要集中在断裂附近。

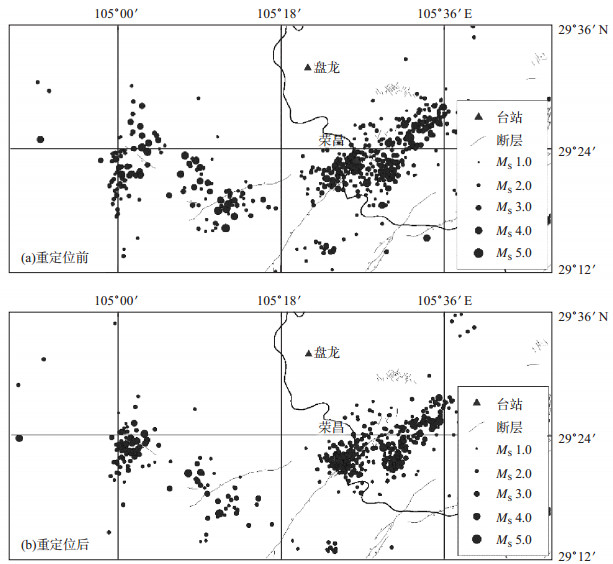
3.1 荣昌地区

图 8为荣昌地区重定位前后震中分布图。如图 8所示, 重定位前地震震中沿华蓥山断裂展布, 但分布较分散。华蓥山断裂走向N40°—45°E, 倾向SE, 倾角30°—70°。重定位后地震震中向断裂形态有所集中, 呈条带状分布。荣昌地区存在开采气体及废井注水等一系列人为干扰活动, 这些干扰活动对该地区的地震活动性存在一定的影响。诱发地震主要发生在采气及注水井附近, 与这些活动的深度相近, 集中在浅部沉积层中。重定位后该地区地震的深度主要集中在10 km以内, 尤其是小震的多分布在5 km附近。王小龙等（2011）研究表明, 该地区地震丛集现象与注水井的位置密切相关; 贺曼秋等（2012）研究认为, 注水活动增加了断层交汇部分的压力, 使得断层强度降低, 继而产生了破裂并诱发地震。该地区地震主要沿断裂分布, 受地质构造控制, 同时该地区人为干扰活动较多, 不排除存在诱发地震的可能。

3.2 巫山地区

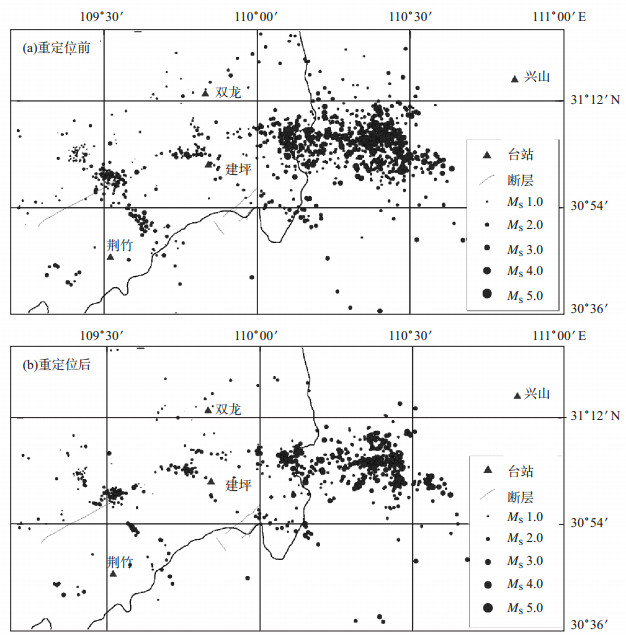
图 9为巫山地区重定位前后震中分布图。如图 9所示, 重定位前, 重庆巫山至湖北巴东地区小震密集, 成团簇状。重定位后, 部分小震在定位过程中被舍弃, 其余地震分布有所集中, 在巴东神农溪呈现出一定的条状分布趋势。震中分布与地层走向一致, 且沿着三峡水库分布。震源较浅, 集中在10 km以内, 平均深度为6 km左右。2006年三峡水库蓄水之前, 该地区地震零星分布（魏红梅等, 2015）。在三峡水库蓄水完成后, 该地区小震频发, 同时3级以上地震数目较之前大幅增加, 且与蓄水深度呈现一定的关联性。对该地区历史地震震中的调查表明, 震中岩溶发育, 可能由于库区水体渗透进入附近的小断层从而诱发一系列地震活动。震中集中区域存在高桥断裂、牛口断裂、水田坝断裂、九畹溪断裂、仙女山断裂等众多小断裂, 张娜等（2018）对三峡地区地震活动的研究表明, 该地区地震多为诱发与构造活动共同作用的结果。

3.3 北碚地区

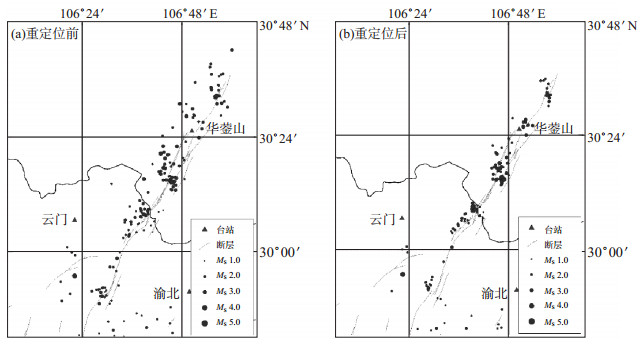
图 10为北碚地区重定位前后震中分布图。如图 10所示, 重定位前, 重庆北碚至四川渠县的地震多分布在华蓥山断裂附近, 与断裂展布形态一致, 倾向SE, 倾角30°—60°, 但分布较分散。重定位后, 震中分布有向断裂集中的趋势, 呈条状分布, 震源深度约为7 km, 地震序列的关联性不强, 具有一定的孤立性。该区地震活动主要受断裂地质活动的影响, 为构造地震, 与人为干扰活动的关联性不大。

3.4 石柱地区

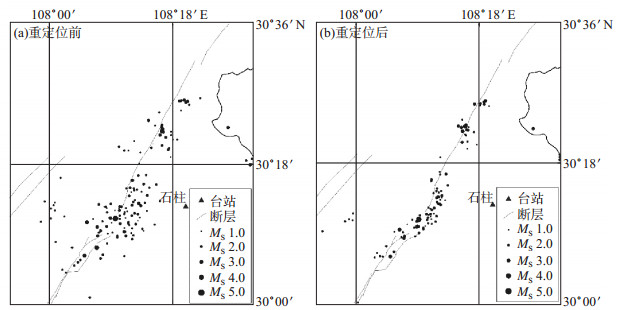
图 11为石柱地区重定位前后震中分布图。如图 11所示, 石柱地区小震较多, 重定位前, 地震主要集中分布在方斗山基底断裂附近, 且分布较分散。方斗山基底断裂为七曜山—金佛山基底断裂的分支, 与其斜交于长寿地区, 倾角70°—80°, 具正断层力学性质, 在石柱地区沉积最大厚度达17 km。重定位后, 震中分布沿方斗山断裂集中, 呈条状分布。震源深度约为7 km, 地震序列的关联性不强, 表明该区地震活动主要受基底断裂地质构造的控制。该区毗邻三峡库区重庆段, 不排除库区蓄水造成该区地震活动性增强的可能。

3.5 武隆地区

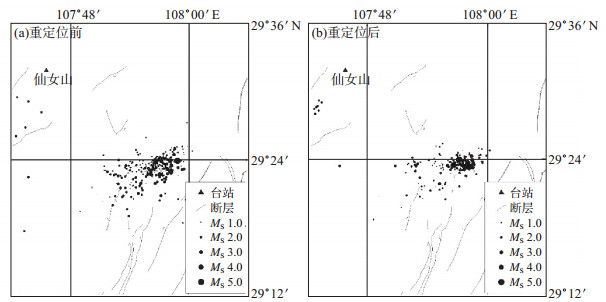
图 12为武隆地区重定位前后震中分布图。如图 12所示, 重定位前, 该地区地震活动主要集中在七曜山—金佛山、彭水2条基底断裂夹持的褶皱束中, 分布较分散, 区域历史地震活动性不强, 2017年11月23日该地区发生了5.0级地震, 地震活动性有所增强。重定位后, 地震分布向此次地震的主震集中, 形成较密集的地震团簇。震源区附近并无已确认的断层构造, 最近的文复断裂距其约5 km, 表明该区的地震活动与该断裂的地下构造有一定的相关性, 同时不排除有潜伏的其他地下构造的可能。

3.6 巫溪地区

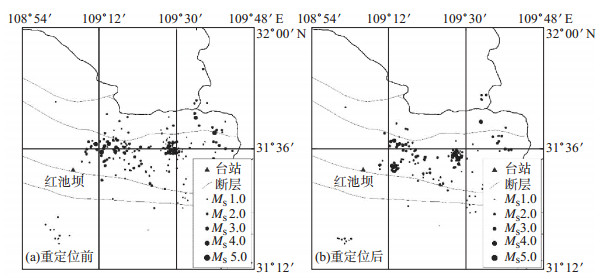
图 13为巫溪地区重定位前后震中分布图。如图 13所示, 该地区地震主要分布在以城口深断裂为主干、巫溪断裂以北的构造区, 断层多数倾向NE, 压性逆冲力学性质, 断裂破碎带显著, 区域地震活动性不强。重定位前, 该区地震主要为小震, 分布在该区的断裂构造附近。重定位后, 地震有向断裂集中的趋势, 因为该区小断裂破碎带较多, 地震分布较分散, 符合该区的地质构造情况。同时, 该区毗邻三峡库区的巫山段, 不排除库区蓄水诱发该区小地震的可能。

3.7 綦江地区

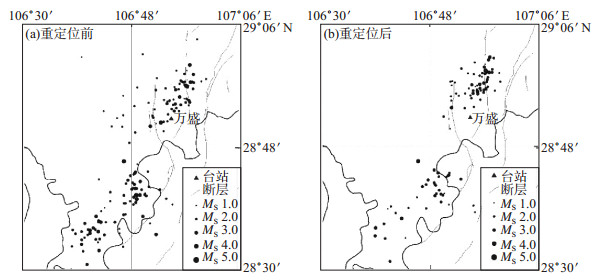
图 14为綦江地区重定位前后震中分布图。如图 14所示, 该地区主要有NS向的长寿—遵义基底断裂和NE向的七曜山—金佛山断裂2条断裂, 它们在綦江万盛附近相交, 造成区域应力场的应力集中, 同时也使得该区成为地震活动分布较集中的地区。重定位后, 该区地震震中有向断裂展布方向集中的趋势, 主要分布在2条断裂的交汇地区, 呈现出一定的条状分布形态, 表明该区地震活动主要受2条断裂地质构造活动的控制。

4 结论

利用Hypo2000定位法与双差定位法分别对重庆及邻区2009年1月至2018年9月的地震序列进行精确定位后, 震源相对位置精度有了显著提高。Hypo2000绝对定位法重定位后深度水平分层现象消失, 地震走时残差均值为0.25 s, 水平误差、垂直误差都有所降低。利用双差绝对定位法重定位后的走时残差基本小于0.30 s, 重定位后沿着平面方向震中位置较Hypo2000方法定位后有所收敛, 向断裂带的分布走向有所聚集。深度上的分层现象进一步消失, 深度为0—12 km的地震分布近似于正态分布, 表明重庆地区的地震震源较浅, 与实际地质构造情况相一致。

在地震活动性方面, 重定位后荣昌、巫山地区地震震中成团簇分布, 与人为干扰活动关联性较强。北碚、石柱地区地震震中向断裂汇集, 呈条状分布, 与断裂构造的关联性较强。武隆地区地震震中汇集, 且不在已知断裂区域中, 疑似震中存在潜伏断裂。巫溪、綦江地区地震震中处于断裂交汇处, 地震活动性与区域地质构造密切相关。