0 引言

直流电阻率测深法作为一种应用广泛而重要的地球物理勘探方法，在能源与矿产勘探、水文及工程勘察中发挥着越来越重要的作用（徐晶，2012）。近年来，随着电子计算机、数字处理等技术的飞速发展，电测深方法在资料处理、正反演计算等方面有了长足进步。虽然直流电测深二维反演已较成熟，且目前发展方向为三维正反演，但一维反演仍具有不可取代的重要作用，如一维反演结果可以作为二维反演的初始模型（欧东新等，2009）。

目前，常用一维电测深反演软件（如RES1D、1X1D等）存在反演误差较大、成图不够美观、无法根据使用者需求修改源代码等问题。笔者基于Matlab，设计一款一维电测深正反演可视化软件。该软件源代码开源，界面简洁友好，反演速度快，结果误差小。使用该软件能够有效提高工作效率，并可得到更加可靠的电性结构参数，进而为相关领域更加深入的研究工作打下良好基础。

1 原理

对于电测深曲线的正演计算，软件中采用递推公式

${T_i} = \frac{{{T_{i + 1}} + {\rho _i}\tan h\left({\lambda {h_i}} \right)}}{{1 + {T_{i + 1}}\tan h\left({\lambda {h_i}} \right)/\rho }} $

(1)

其中，T_i为第i层的电阻率转化函数；ρ_i为第i层电阻率；h_i为第i层厚度；λ为常数。利用20点汉克尔滤波系数，将电阻率转化函数T₁转化为所求的视电阻率ρ_t。

软件使用最小二乘法进行反演。电测深反演可归结为：寻找模型m，以使得目标函数φ趋于极小，公式如下

$ \varphi = \sum {{{\left({{\rho _{{\rm{s}}i}} - {\rho _{{\rm{t}}i}}\left(m \right)} \right)}^2}} $

(2)

其中，ρ_si为第i个极距的实测视电阻率；ρ_ti为由模型m正演计算所得第i个极距的理论视电阻率。反演过程采用奇异值分解法，对线性方程组进行求解。当实测视电阻率与理论视电阻率的相对误差小于阈值时，认为反演所得模型可以采用。

2 软件功能及使用

软件主要包含3个功能，即正演拟合、直接反演和相关系数计算功能。

2.1 正演拟合

在软件界面上点击“导入实测数据”按钮，选择需导入的实测电测深数据文件，根据实测曲线，在“电性结构模型”区域手动调整模型参数。点击“正演拟合法”按钮，软件根据输入的模型参数，正演拟合得到理论观测数据，并显示实测曲线和拟合曲线对比图及二者相对误差（图 1），使用者可重复调整模型参数进行拟合，直至结果满足需求。每次拟合后，软件自动将正演模型保存到zymodel.txt文件，将由该模型正演得到的理论观测数据保存到zyresult.txt文件，将实测曲线与拟合曲线对比图保存到zyfigure.jpg文件。

2.2 直接反演

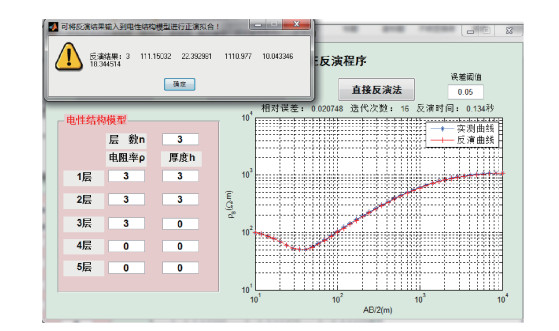
在软件界面上点击“导入实测数据”，选择实测电测深数据文件，设置误差阈值和初始模型，点击“直接反演法”，反演得到测区电性结构模型参数以及由该模型正演拟合得到的理论观测数据。软件界面上将显示实测曲线与拟合曲线对比图及二者相对误差（图 2）。软件自动将反演得到的模型参数保存到fymodel.txt文件，将由该模型正演得到的理论观测数据保存到fyresult.txt文件，将实测曲线与拟合曲线对比图保存到fyfigure.jpg文件。

2.3 相关系数计算

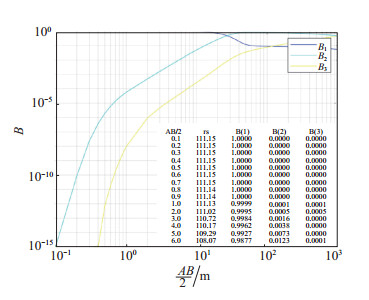
对相关系数的计算包含在前2个功能之中。每次点击“正演拟合法”或“直接反演法”按钮，均会自动计算对应模型在不同极距下的地电阻率理论观测值和每层影响系数，并将结果保存在zybval.txt或fybval.txt文件中，同时绘制各层影响系数曲线（图 3）。

3 软件测试

在不修改电性结构模型参数的情况下，软件会将所有层参数设为3，并作为初始模型进行反演。为了探讨初始模型对反演结果的影响，笔者对常见的3层、4层电性结构模型进行测试，结果如下。

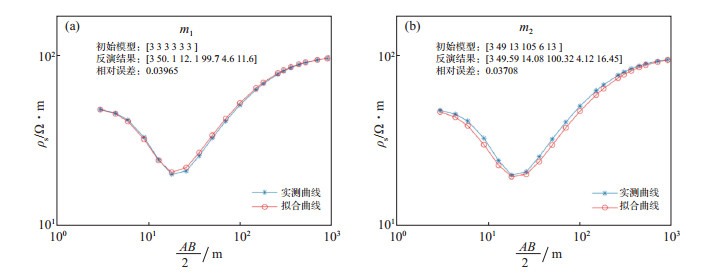
利用理论模型m = [3 50 10 100 5 10]（模型参数含义：层数第1层电阻率值第2层电阻率值第3层电阻率值第1层层厚第2层层厚），正演得到一系列不同极距下的理论观测数据，加入5%的高斯误差后，分别采用初始模型m₁ = [3 3 3 3 3 3]和初始模型m₂ = [3 49 13 105 6 13]进行反演，可得到m₁反演结果与理论值间的相对误差为0.039 65，m₂反演结果与理论值间的相对误差为0.037 08（图 4）。

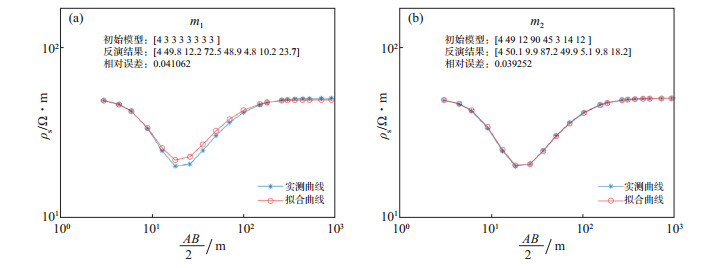
利用理论模型m = [4 50 10 100 50 5 10 15]，正演得到一系列不同极距下的理论观测数据，并加入5%的高斯误差，分别采用初始模型m₁ = [4 3 3 3 3 3 3 3]和初始模型m₂ = [4 49 12 90 45 3 14 12]进行反演，得到m₁反演结果与理论值间的相对误差为0.041 062，m₂反演结果与理论值间的相对误差为0.039 252（图 5）。

综上，无论在3层还是4层电性结构模型下，初始模型的优劣均对反演结果影响不大，但选择较好的初始模型会使反演结果的误差更小。在加入5%的高斯误差后，反演结果与理论结果间的相对误差均小于5%，说明软件运行所得结果稳定可靠。

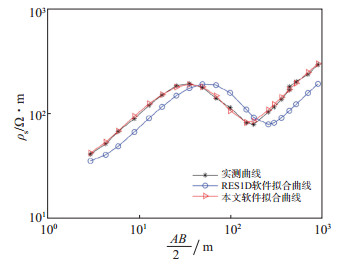
4 实测数据反演

利用常用的RES1D软件和本文介绍的Matlab可视化软件对2009年5月23日昌黎县后土桥的电测深数据（NE17°方向）进行反演，并对反演结果进行对比分析（图 6）。RES1D软件反演结果为m₁ = [4 32.36 573.02 40.07 768.79 3.9 18.8 140.02]，相对误差为0.121 9；本文软件反演结果为m₂ = [4 33.39 498.13 35.26 955.43 2.59 14.24 72.93]，相对误差为0.047 8。

由图 6可见，RES1D软件反演结果m₁模型和本文软件反演结果m₂模型均反映出后土桥NE17°电测深曲线为KH型，且与实测曲线拟合较好，故反演结果具有一定可信度。相比而言，本研究软件反演结果拟合度更高。在实际工作中，由于测量误差和问题的非线性等原因造成解的非唯一性，且等值作用的存在使反演结果具有多解性。因此，应尽量减小测量误差，并结合地质资料，在等值范围内求出合理解。

5 结束语

文中基于Matlab设计一款一维电测深正反演可视化软件，相比常用的RES1D等软件，该软件源代码开源，可根据需求修改参数，界面简洁友好，图片更为美观。软件对初始模型的依赖较弱，反演速度快，结果误差小，还可自动计算不同极距下各层的影响系数，可直接用于测区地电阻率数值计算。经测试，该软件功能达到预期目的，值得推广使用。