2. 中国天津 300201 天津市地震局
2. Tianjin Earthquake Agency, Tianjin 300201, China
长期地震监测预报实践和科学研究证明,与地震孕育发生有关的震兆信息要求观测环境噪声背景低,以产出观测精度高、长期连续可靠的观测数据。目前国内大多数地电阻率观测台站场地均存在一定程度的电磁干扰,其中:工频干扰对观测系统的影响被抑制在规范允许范围内;非工频干扰中城市轨道交通(如地铁、轻轨)影响最大,范围可达数十千米(徐学恭等,2008)。如何抑制轨道交通对地电观测的干扰,已成为地电观测学科的研究热点(赵家骝等,1997;谢凡等,2011)。
小波变换和HHT(Hilbert-Huang Transform,希尔伯特-黄变换)方法是非平稳信号的时频分析工具,在地震电磁数据处理中得到广泛应用,如:宋治平等(2004)证明,小波变换可作为电磁数字化资料分析处理的有效方法;邱颖等(2009)利用小波域阈值滤波方法,对地电场秒采样信号中叠加地电阻率人工供电干扰信号进行分析和处理;安张辉等(2010)将HHT方法用于地电场观测数据处理,较好地分析并认识其频谱特征;李伟等(2013)通过小波变换方法分解地电场观测原始信号,分析环境噪声对原始观测数据的影响强度。
对于地电阻率观测的干扰研究,张磊等(2010)对全国7个地震台站地电阻率观测干扰源进行汇总,分析天津塘沽地震台津滨轻轨铁路干扰,并建议采用非平稳信号的时频分析方法;张世中等(2013)对受轨道交通干扰的地电阻率测量背景电位差数据进行FFT变换和功率谱分析,认为城市轨道交通运行干扰能量集中在50-250 s,并提出采用非干扰时段数据均值代替日均值的抗干扰措施和建议。该处理方式较为简单且易实现,但观测信号信噪比被降低。本文以津滨轻轨干扰的典型台站--塘沽地震台地电阻率观测数据为例,采用小波和HHT方法进行滤波处理,对比2种方法的优缺点,以取得更好的滤波效果。
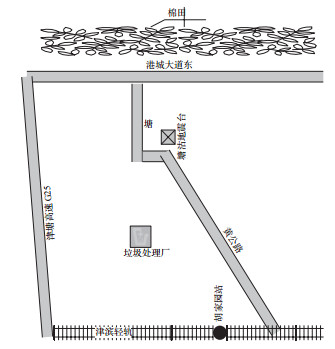
1 轻轨干扰天津塘沽地震台(下文简称塘沽台)位于津滨轻轨铁路以北,垂直距离约6 km,台站相对位置见图 1。津滨轻轨2004年3月28日运营,列车运行时间为早6时至晚22时30分,在此时段,塘沽台地电阻率观测受到较大干扰,数据跳变达2%-7%,淹没地震前异常信息,见图 2。按照观测要求,地电阻率观测误差应不超过0.3%(杜玮,2004)。因此,难以直接从受轻轨干扰的塘沽地电阻率观测资料中检测到与地震孕育过程相关的异常信息。
|
图 1 塘沽地震台相对位置 Fig.1 Relative location of Tanggu Seismic Station |

|
图 2 塘沽地电阻率观测数据轻轨干扰曲线 (a) 2个月观测数据;(b) 5日观测数据 Fig.2 The curve of Tanggu geo-resistivity observation data disturbed by subway |
选取塘沽台某日地电阻率观测数据进行方差分析,结果见图 3、表 1。在00:00-05:00时段和06:00-23:00时段,原始观测数据存在明显差异,见图 3(a)。分析NS、EW向地电阻率小时值变化(最大值与最小值之差)与全天平均值的比值,可知NS向为5.835%,EW向为1.025%。小时值相对方差明显变大,见图 3(b),其中NS向相对方差由00:00-05:00时段平均0.031%变为06:00-23:00时段的7.36%,变化幅度达237.4倍;EW向相对方差由平均0.077%(00:00-05:00)变为1.34%(06:00-23:00),变化幅度达17.4倍。

|
图 3 塘沽台某日地电阻率观测原始数据及相对方差曲线 (a)原始曲线;(b)相对方差曲线 Fig.3 Geoelectric resistivity observation and its relative variance in one day at Tanggu Seismic Station |
| 表 1 塘沽台某日两时段地电阻率观测值相对方差比较 Table 1 Contrast between relative variances of observed geoelectric resistivity data during two time periods one day at Tanggu Seismic Station |
小波包变换是小波变换的进一步完善与发展。在小波去噪过程中,仅对小波分解的每层低频系数进行分解,而细节系数向量(高频系数)不再分解,导致部分高频信息丢失。而在小波包分解中,每层分解所得向量均使用近似系数向量分解的方法分为低频系数和高频系数向量2部分。因此,小波包分解克服了小波分解在高频段频率分辨率和在低频段时间分辨率较差的问题,是一种更精细的信号分析方法,可提高信号的时频分辨率(程正兴等,2007)。诸多研究表明,高频信号依然可能存在有用信息(杜方等,2004;于晨等,2017),为了防止高频部分信息的过多丢失,使用小波包分解实现观测信号的降噪处理。
基于正交小波变换的阈值降噪方法是一种实现简单、效果较好的小波去噪方法,是小波分析在信号降噪处理中的主要滤波方法,对于非平稳信号滤波具有较好效果。阈值去噪方法的思想是,对小波分解后各层系数中模大于或小于某阈值的系数分别处理,然后进行反变换,重构去噪信号。
在阈值去噪过程中,小波基和分解层数的选择、阈值选取规则和阈值函数设计,均为影响最终去噪效果的关键因素(高静怀等,1996;杜文辽等,2010)。文中以降噪信号的信噪比为选取准则,确定最优基和分解层数,即根据信号特点和实验效果进行反复测试验证,选择db4(Daubechies)作为最佳基,分解层数为5,以极大极小准则阈值选择规则确定阈值。
2.2 EMD分解和EMD尺度滤波希尔伯特-黄变换(Hilbert-Huang Transform,简称为HHT)法(Huang et al,1998)是一种全新的信号处理方法,对于非线性、非平稳信号处理具有清晰的物理意义,能够得到信号的振幅-时间-频率分布特征。HHT变换将时间信号通过经验模态分解(empirical mode decomposition,EMD)成为一组固有模态函数(intrinsic mode function,IMF),进行Hilbert变换,得到Hilbert谱,即可描绘出信号的时频图、时频谱和幅值谱。由于HHT变换在分解的过程中不需要预设基函数,可以依据信号自身时间尺度特征进行模态分解,并保留数据自身特性,且具有自适应性。
IMF的定义必须满足2个条件:①在整个信号包络中,极值点与零点的数量相等或最多相差一个;②在任意一个局部范围内,极大值点确定的包络和极小值点确定的包络均值为0,即关于时间轴近似对称。
EMD是以IMF为基函数的时域分解方法,认为信号由IMF分量信号叠加而组成,因此对所有信号均可进行EMD分解。EMD分解的一种方法过程如下(安张辉等,2010):①遍历信号x(t),标记信号的所有极值点;②利用拟合函数将极大值点和极小值点分别拟合,得到xmax(t)、xmin(t)2条包络曲线;③计算包络线均值m1(t) = [xmax(t) + xmin(t)]/2;④定义h1(t) = x(t) - m1(t),当h1(t)满足IMF的条件时记为模态输出c1(t);⑤若h1(t)不满足IMF的条件,重复以上循环,直至满足条件。EMD分解结果公式如下
| $ x(t) = \sum\limits_{i = 1}^n {{c_i}} (t) + {r_n}(t) $ | (1) |
式中,x(t)为信号,ci(t)为第i次分解出的IMF分量,rn为残余项。
2.3 滤波效果评价标准文中尝试采用小波滤波方法、EMD滤波方法及EMD与小波相结合的滤波方法,将信噪比和方差作为滤波效果评价标准(胡广书,2004),对比分析3种方法的滤波效果。
2.3.1 信噪比信噪比定义为
| $ {\rm{SNR}} = 10\lg \frac{{\frac{1}{n}\sum\limits_n {{f^2}} (i)}}{{\sum\limits_n {{{\left[ {f(i) - {f^\prime }(i)} \right]}^2}} /n}} $ | (2) |
式中,f (i)为不含噪声的原始信号,f′(i)为滤波去噪信号。
2.3.2 方差去噪后信号方差Rmes定义为
| $ R_{\mathrm{mes}}=\sqrt{\frac{\sum\left[f(i)-f^{\prime}(i)\right]^{2}}{n}} $ | (3) |
式中,f (i)为原始信号,f′(i)为滤波去噪信号。
3 数据处理选取塘沽台2014年1-6月地电阻率观测数据,分别采用小波阈值滤波和小波包阈值滤波方法,对轻轨干扰数据进行降噪处理,并通过均方误差和信噪比,对比分析滤波结果。
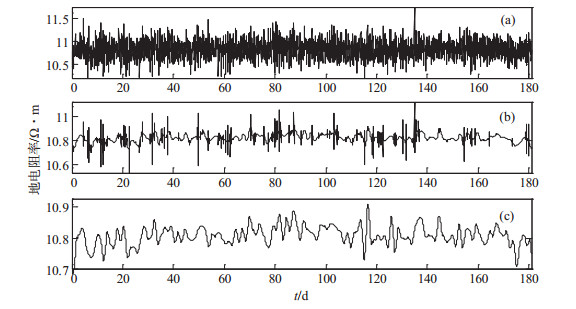
3.1 小波滤波处理选取2014年1-6月塘沽台地电阻率观测数据,采用小波函数db4分解到第5层,分别进行小波阈值滤波和小波包阈值滤波处理,对比分析结果见图 4,可知小波包阈值滤波结果明显优于小波阈值滤波结果。引入均方误差,可验证小波包阈值滤波方法的优越性,结果见表 2,明显可见小波包阈值滤波均方误差偏小。
|
图 4 NS向地电阻率小波及小波包阈值滤波结果 (a)NS向原始数据曲线;(b)小波阈值滤波;(c)小波包阈值滤波 Fig.4 Wavelet and wavelet packet threshold filtering results of geo-resistivity observation data |
| 表 2 小波及小波包阈值滤波均方差 Table 2 Mean square difference of wavelet threshold and wavelet packet threshold filtering |
为了避开城市轨道交通运行干扰,在数据处理时,张世中等(2013)提出:分析短时间段(若干天)地电阻率变化,应舍弃干扰时间段(06:00-23:00)数据;分析长时间段(月、年)地电阻率变化,可采用由每天24小时观测数据计算得到的日均值数据。由于地电阻率的采样率为1/3 600 Hz,即一小时记录一个观测值。若只保留00:00-05:00时段的观测数据,则将损失75%的观测数据,对于震兆异常信息的提取不利。
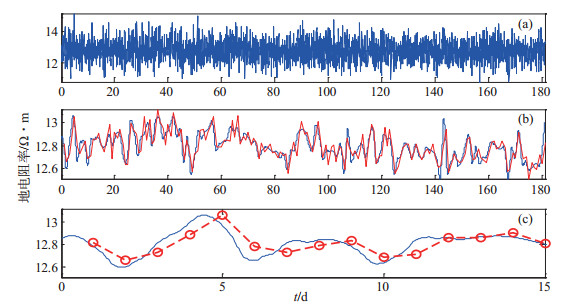
为保留观测信息,对塘沽台2014年1-6月地电阻率观测数据的干扰时段(06:00-23:00)和全天时段分别进行滤波处理,即分别对干扰时段(06:00-00:23)(设为A)、全天时段(00:00-23:00)(设为B)数据进行滤波和日均值处理(设为C),并计算各类数据信噪比,对比日均值和小波包阈值滤波方法的滤波效果,结果见图 5、图 6、表 3。

|
图 5 干扰时段小波阈值滤波与日均值对比结果 (a)EW向原始数据曲线;(b)仅对干扰时段小波包阈值滤波与日均值对比;(c)15天结果对比 Fig.5 The comparisons of wavelet packet threshold filtering results of interference period with daily means results |
|
图 6 全天时段小波阈值滤波与日均值对比结果 (a)小波阈值滤波;(b)小波包阈值滤波与日均值处理对比;(c)15天的结果对比 Fig.6 The comparisons of wavelet packet threshold filtering results with daily means results of the whole day |
| 表 3 不同处理方式下塘沽地电阻率信噪比 Table 3 The signal to noise ratio of ground resistivity in Tanggu under different treatments |
图 5(b)中蓝线所示为采用小波包阈值滤波方法仅对干扰时段(06:00-00:23)数据处理结果,红线为日均值,图 5(c)所示为处理结果对比的放大效果。图 6(b)中蓝线所示为采用小波包阈值滤波方法对全天小时值处理结果,红线为日均值。图 6(c)为处理结果对比的放大效果。由图 5、图 6、表 3可知:小波包阈值滤波和日均值曲线一致性较好;采用小波包阈值滤波算法,干扰数据是否分段处理对滤波结果的信噪比影响较小;采用小波包阈值滤波方法进行数据处理,滤波效果明显优于日均值,且信噪比高,观测资料质量明显提高。
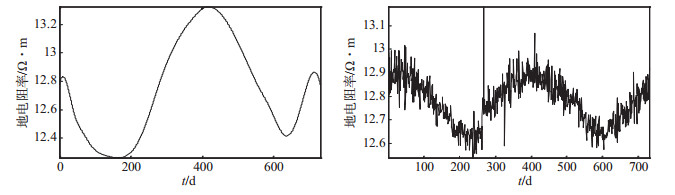
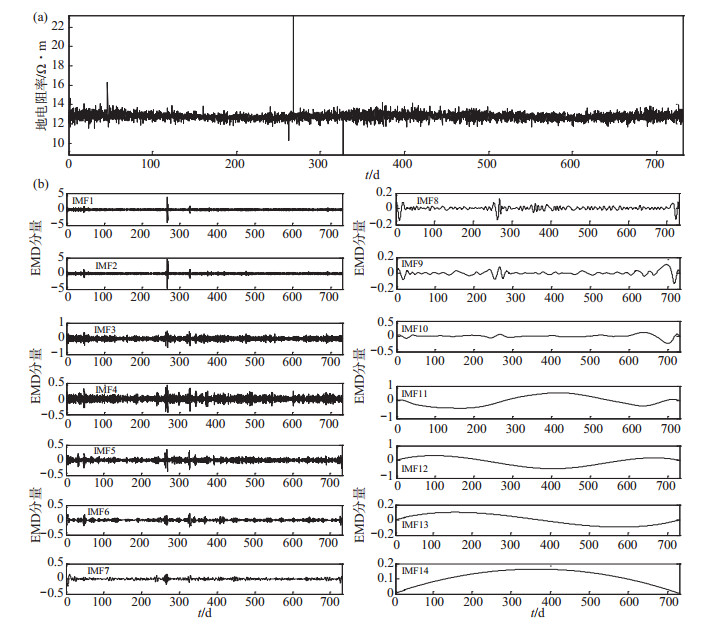
3.2 EMD滤波方法对信号进行EMD尺度滤波,实质是从IMF中剔除扰动干扰的IFM分量。选取2007-2008年地电阻率观测数据,进行EMD尺度滤波及EMD分解,结果见图 7、图 8。
|
图 7 EMD滤波结果与日均值对比 Fig.7 Comparison between filtering results of EMD and mean values |
|
图 8 2007-2008年塘沽台地电阻率观测数据EMD分解 (a)原始信号;(b)EMD分解 Fig.8 EMD decomposition of Tanggu geo-resistivity observation data from 2007 to 2008 |
图 7中(a)图为EMD尺度滤波曲线,(b)图为日均值曲线,对比可知,EMD尺度滤波对轻轨干扰滤波效果较好,且年变信息保留较为准确,但二者极值大小有偏差,使得2种方法的处理结果在形态上有一定区别。造成这种差别的原因是,EMD分解的IMF分量是信号所有极大值、极小值包络的平均值,且滤波结果由符合滤波条件的IFM分量组合而成,若信号出现较大突跳,将造成极值包络的变化,进而影响分解结果及EMD尺度滤波的结果。由图 8(a)可见,塘沽地电阻率NS向原始数据出现数值较大突跳点,影响了EMD分解精度,从而影响EMD滤波结果的幅值。
4 结论与讨论选取受天津轻轨干扰的塘沽台地电阻率观测数据进行滤波实验,将小波方法、HHT方法的滤波结果与日均值进行对比,并结合信噪比和均方差讨论滤波效果,结果表明:①小波包阈值滤波与日均值处理结果一致性较好,且信噪比提高;②EMD滤波是基于信号形态的滤波方法,若信号中存在较大突跳,则对EMD滤波结果产生较大影响;③对比日均值,小波包阈值滤波方法将数据利用率提高了75%,有利于震兆信息提取。
综合分析,基于小波变换的滤波方法更加稳定,信噪比较高,观测资料质量提高。应用地电阻率观测资料时,若要求高信噪比,小波包阈值滤波方法可为有效途径之一。
安张辉, 元丽华, 李宁, 等. 2010. HHT方法在地电场数据处理中的应用[J]. 地球物理学进展, 25(2): 525-532. DOI:10.3969/j.issn.1004-2903.2010.02.020 |
程正兴, 杨守志, 冯晓霞. 2007. 小波分析的理论算法进展和应用[M]. 北京: 国防工业出版社.
|
杜方, 吴江.川滇强震前短临综合前兆时间、空间特征研究[C]//中国地震学会第十次学术大会论文摘要专集.北京: 中国地震学会, 2004: 38.
|
杜文辽, 朱茹敏, 李彦明. 2010. 小波滤波分解层数的自适应确定方法[J]. 光电子·激光, 21(9): 1408-1411. |
杜玮. 2004. 《地震台站观测环境技术要求》宣贯教材[M]. 北京: 地震出版社, 90-130.
|
高静怀, 汪文秉, 朱光明, 等. 1996. 地震资料处理中小波函数的选取研究[J]. 地球物理学报, 39(3): 392-400. DOI:10.3321/j.issn:0001-5733.1996.03.013 |
胡广书. 2004. 现代信号处理教程[M]. 北京: 清华大学出版社.
|
李伟, 马钦忠, 宋志平, 王冠玥. 2013. 小波变换在地电场数据分析中的应用[J]. 地震学报, 35(1): 26-35. DOI:10.3969/j.issn.0253-3782.2013.01.004 |
邱颖, 席继楼. 2009. 小波方法在地电场干扰处理中的分析研究[J]. 地震地磁观测与研究, 29(2): 57-63. DOI:10.3969/j.issn.1003-3246.2009.02.009 |
宋治平, 武安绪, 马钦忠, 等. 2004. 小波分析在电磁数字化资料分析处理中的应用[J]. 西北地震学报, 26(1): 38-43. |
谢凡, 滕云田, 胡星星, 等. 2011. 地磁台站的城市轨道交通干扰的小波抑制方法研究——以天津轨道交通干扰为例[J]. 地球物理学报, 54(10): 2698-2707. DOI:10.3969/j.issn.0001-5733.2011.10.027 |
徐学恭, 田山, 韩润泉, 等. 2008. 津滨轻轨地磁干扰范围的实验研究[J]. 地震地磁观测与研究, 29(6): 41-44. DOI:10.3969/j.issn.1003-3246.2008.06.008 |
于晨, 卢军, 解滔, 等. 2017. 基于概率密度分布的地电场地震前兆异常提取方法[J]. 地震, 37(4): 22-36. |
张磊, 关华平, 田山, 等. 2010. 地电阻率观测各类干扰源的分析与研究[J]. 地震地磁观测与研究, 31(2): 68-76. DOI:10.3969/j.issn.1003-3246.2010.02.012 |
张世中, 石航, 王兰炜, 胡哲, 刘大鹏, 魏连生, 鞠永. 2013. 地电台站受城市轨道交通干扰的测试分析与抗干扰措施研究[J]. 地震学报, 35(1): 117-124. DOI:10.3969/j.issn.0253-3782.2013.01.012 |
赵家骝, 王燕琼, 关华平, 唐九安, 武华峰. 1997. 电气化铁路对平凉地震地电观测干扰的实验研究[J]. 地震, l7(2): 212-220. |
Huang N E, Zheng S, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc R Sco Lond, 545(1 971): 903-995. |
 2019, Vol. 40
2019, Vol. 40

