2. 中国三河 065201 防灾科技学院;
3. 中国武汉 430071 中国地震局地震研究所;
4. 中国四川 610000 成都理工大学
2. Institute of Disaster-Prevention, Sanhe 065201, China;
3. Institute of Seismology, China Earthquake Administration, Wuhan 430071, China;
4. Chendu University of Technology, Sichuan Province 610000, China
在海岸观测海水面运动时,容易发现海水面每天有1次或者2次周期性涨落。19世纪末,科学家怀疑,当起潮力对地球的固体部分发生作用时,固体部分也会发生周期性变化。1876年,开尔文(Kelvin)为了估算地球在太阳、月亮起潮力作用下发生形变的量级,假设了一个最简单的地球模型——球状无海洋不旋转均匀不可压缩模型,检验该模型对引潮力的响应。考虑到刚体地球在引潮力的影响下不会发生形变,在开尔文地球模型上覆盖一层海水,并研究引潮力影响下海水表面各点的变形,此为平衡潮理论。1882年,英国人达尔文(Darwin)将当时的海潮观测资料与平衡潮理论值进行对比,发现观测值与理论值的潮高比值为0.68,表明地球在起潮力作用下发生形变,升降幅度为海潮平衡潮潮高的1/3,该形变即为固体潮(方俊,1984;吴庆鹏,1997;朱平,2005),是在月球、太阳和其他星体作用下地球发生的周期性形变。固体潮种类较多,例如倾斜固体潮、重力固体潮、应变固体潮等(徐华君等,2006)。
随着观测技术的提高,现代大地测量观测精度大幅提升,发现地球的潮汐形变对固定在地球表面的任何观测(如重力、倾斜、应变、水准测量等)均有影响。此外,现代大地测量技术的飞速发展依赖于空间对地观测技术的进步,地球的潮汐形变导致地球内部物质的重新分布,从而产生扰动附加位,引起对地观测卫星(尤其是近地卫星)轨道的扰动(许厚泽,2010)。因此,地球潮汐观测对于国家的基础测绘、空间技术发展和卫星定轨等具有重要意义,确定固体潮理论值显得尤为重要(许厚泽等,1997;王谦身,2003)。就当前而言,在种种导致固体地球变形的原因(比如板块移动、冰川和海水的压力、岩石圈的构造活动等)中,由于已知的引力潮影响,地球潮汐活动引起的固体地球变形作用力是唯一可以预先通过理论计算得到的,如:万永革等(2006)利用Visual Basic,实现了以波形图方式输出某一地区重力固体潮理论值的功能;徐华君等(2009)仿真实现了全球重力固体潮在二维和三维尺度上的可视化功能。
文中利用改进的新计算方法进行Matlab编程,采用GUI进行可视化,以波形图和Excel的形式计算输出某一地区的重力固体潮理论值,并在此基础上,实现未来24小时全球重力固体潮仿真模拟,直观观察固体潮在地面的时空变化规律,为固体潮研究提供有利平台。
1 重力固体潮理论值计算引潮力的垂直分量使地球表面重力发生变化,称之为重力固体潮。重力固体潮理论值可利用天顶距直接计算或利用分波法计算(赵晓燕等,1997)。文中采用天顶距方法计算重力固体潮理论值,通过董良等(2015)提出的新参数和新方法,在Matlab软件中利用以下方式改进计算程序:①采用Matlab自带函数计算儒略日;②采用最新公布的J2000系统(郗钦文等,1986)计算天文参数;③改变计算地心纬度公式,使其更加有物理意义。
1.1 引潮力和引潮力位把作用在地球随机一点的引潮力定义为,日、月及其他天体对地心的引力与对随机点的引力之差的绝对值。引潮力是引潮力位的梯度,与时间及在地球上的经纬度有关(郜晓亮,2009)。则月球、太阳的起潮力位Vn计算公式如下
| $ V_n^{\rm{m}} = \frac{{GM}}{{{d_{\rm{m}}}}}\sum\limits_{n = 2}^\infty {{{\left({\frac{r}{{{d_{\rm{m}}}}}} \right)}^n}} {{\rm{P}}_n}\left({\cos {z_{\rm{m}}}} \right) $ | (1) |
| $ \cos {z_{\rm{m}}} = \sin \varphi \sin {\delta _{\rm{m}}} + \cos \varphi \cos {\delta _{\rm{m}}}\cos {H_{\rm{m}}} $ | (2) |
| $ V_n^{\rm{s}} = \frac{{GS}}{{{d_{\rm{s}}}}}\sum\limits_{n = 2}^\infty {{{\left({\frac{r}{{{d_{\rm{s}}}}}} \right)}^n}} {{\rm{P}}_n}\left({\cos {z_{\rm{s}}}} \right) $ | (3) |
| $ \cos {z_{\rm{s}}} = \sin \varphi \sin {\delta _{\rm{s}}} + \cos \varphi \cos {\delta _{\rm{s}}}\cos {H_{\rm{s}}} $ | (4) |
式中,G为重力固体潮理论值;dm、ds分别为月心、日心到地心的距离;zm、zs分别为月球、太阳对p点的地心天顶距;φ为p点地理纬度;M、S分别表示地球、太阳的总质量;r表示地球内某点到地心的距离,是地球内位置函数;δm、δs分别为月球、太阳的赤纬;Hm、Hs分别为月球、太阳的地方时角;Pn表示勒让德多项式。
1.2 计算原理对引潮力位进行拉普拉斯展开,一般对太阳引潮力位进行二阶展开,月亮引潮力位进行二、三阶展开,得到重力固体潮理论值。重力固体潮理论值计算公式(中国科学院地质研究所计算组,1974)如下
| $ \begin{array}{l} G = - 165.17F(\varphi){\left({\frac{{{c_{\rm{m}}}}}{{{d_{\rm{m}}}}}} \right)^3}\left({{{\cos }^2}{z_{\rm{m}}} - 1/3} \right) - 1.37{F^2}(\varphi){\left({\frac{{{c_{\rm{m}}}}}{{{d_{\rm{m}}}}}} \right)^4}\left({5{{\cos }^3}{z_{\rm{m}}} - 3\cos {z_{\rm{m}}}} \right)\\ \;\;\;\;\;\; - 76.08F(\varphi){\left({\frac{{{c_{\rm{s}}}}}{{{d_{\rm{s}}}}}} \right)^3}\left({{{\cos }^2}{z_{\rm{s}}} - 1/3} \right) \end{array} $ | (5) |
式中,G为重力固体潮理论值,单位为cm/s2(1 μcm/s2= 1 μGal);cm、cs为月亮、太阳到地心的平均距离;φ为p点地理纬度。
按照中华人民共和国地质矿产行业标准·大比例尺重力勘探规范(DZ/T0171—1997)(中华人民共和国地质矿产部,1997),使用董良等(2015)给出的新参数,根据公式(5)计算重力固体潮理论值,所得结果更为准确、可靠。具体计算步骤如下。
(1) F(φ)为地球上任意一点到地心的距离与地球半径的比值,是关于地理纬度的函数,根据台站地理纬度φ,得
| $ F(\varphi) = 0.998327 + 0.00167\cos (2\varphi) $ | (6) |
(2) 采用Matlab自带的儒略日计算函数,计算儒略日T0和儒略世纪数T,得
| $ {T_0} = {\rm{ juliandate }}({\rm{y}}, {\rm{m}}, {\rm{d}}, {\rm{t}}, {\rm{min}}, {\rm{sec}}) $ | (7) |
| $ T = \frac{{{T_0} - 2451545.0 + (t - \delta)/24}}{{36525}} $ | (8) |
其中,2451545.0指起算时间为2000年1月1日12时,t为北京时间(单位为小时),δ为所在地时区。
(3) 采用J2000.0系统计算6个天文参数,具体计算公式见表 1。
| 表 1 6个天文参数的计算公式 Tab.1 Calculation formula with 6 astronomical parameters |
(4) 根据6个天文常数计算月亮、太阳参数c/r和cosz。地方恒星时θ为
| $ \theta = (t - \delta ) \times 15^\circ + h + L - 180^\circ $ | (9) |
地理纬度φ转换成地心纬度φ的公式(张少泉,1985)为
| $ \varphi = \arctan {(1 - 1/298.256)^2}\tan (\varphi) $ | (10) |
根据表 1给出的公式,计算月亮参数cm/dm、coszm和太阳参数cs/ds、coszs。详细计算公式郜晓亮(2009)已给出。
将所得F(φ)、cm/dm、coszm、cs/ds、coszs代入公式(5),计算重力固体潮理论值。
2 重力固体潮可视化实现Matlab是一种高级程序开发语言,拥有开发算法、数据分析和实现可视化等功能,可提供简洁实用的图形用户界面(GUI)工具。由于GUI简单易上手的特性,容易满足非专业用户需求,无需深入学习编程知识,即可通过窗口、菜单方便地进行操作,便于科研和工程工作的开展(施晓红等,2003)。使用Matlab中的GUI工具实现视觉化编程,主要环节如下:利用Guide软件设计GUI外观,即设置所需控件与菜单等,对相应菜单和控件的Callback函数进行编程(樊华等,2014)。
2.1 Matlab GUI程序设计流程在Matlab中创建一个Matlab GUI界面,添加控件,包括静态文本、按钮控件和编辑框控件,拖动控件,创造一个良好的界面更利于使用,在不同控件中添加代码,即写回调函数,该函数在程序运行时开始执行。Matlab GUI程序设计流程见图 1。设计界面并完成编程后,打开界面,输入信息即可得到结果。文中设计的程序需要完成以下任务:①在界面中输入时间、经纬度,确定采样频率,得到某时段内重力固体潮理论值,并以图像展示;②在界面中输入时间,得到未来24小时全球重力固体潮动态模拟图。

|
图 1 Matlab GUI程序设计流程 Fig.1 Flow chart of Matlab GUI programming |
该程序还需具备3个附加功能:①程序运行时显示进度条;②数据输入错误时提示框;③以Excel形式输出某时段重力固体潮理论值。
2.2 功能实现程序界面设计要求简单易懂,使用Matlab GUI程序,设计完成重力固体潮理论值计算程序界面。该界面友好,便于研究者使用。此处给出Matlab R2014a版本的演示界面,见图 2。
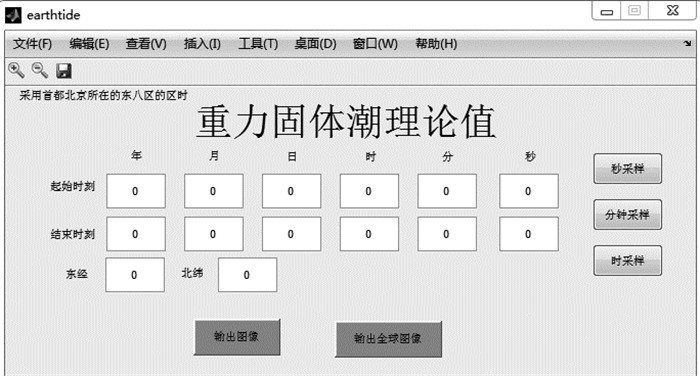
|
图 2 重力固体潮理论值计算程序界面 Fig.2 Interface of theoretical calculation of gravity earth tide |
在实现主要功能时,考虑到快速识别输入会遇到的问题以及知晓程序运算速率等因素,设计3个附加功能,使程序更加便利,如:当程序运行时显示进度条,见图 3(a);在数据输入错误时予以提示,见图 3(b);以Excel形式输出某时段内重力固体潮理论值,见图 3(c)。
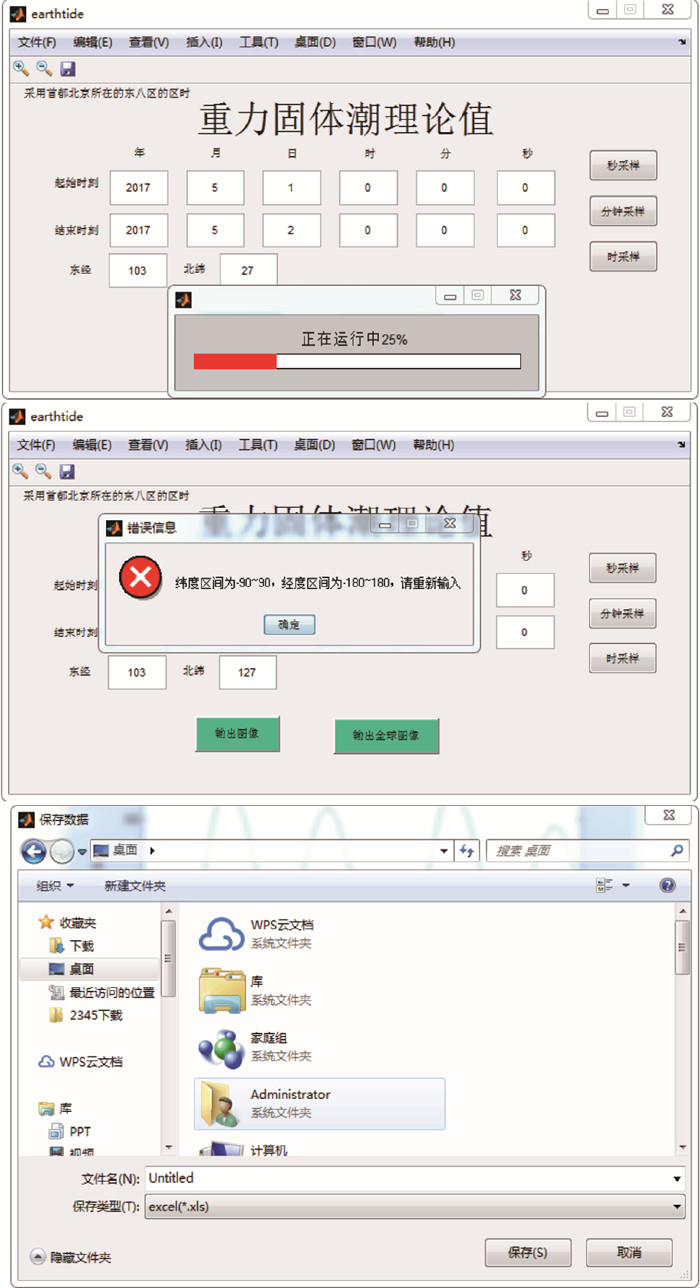
|
图 3 附加功能实现 (a)运算时显示进度条;(b)输入错误后提示;(c)以Excel格式输出数据 Fig.3 Implementation of additional functions |
设固定点位(103°E,27°N),采样率分别为秒采样、分钟采样、时采样,计算一天、一个月、半年的重力固体潮理论值,采用重力固体潮理论值计算程序输出图像,见图 4,其中:①采样间隔为秒采样,计算得到2017年5月1日重力固体潮理论值,输出图像见图 4(a);②采样间隔为分钟采样,计算得到2017年4月1日至2017年5月1日重力固体潮理论值,输出图像见图 4(b);③采样间隔为时采样,计算得到2017年1月1日至7月1日的重力固体潮理论值,输出图像见图 4(c)。

|
图 4 同一参考点不同采样率不同周期重力固体潮理论值 (a)秒采样一天图像;(b)分钟采样一个月图像;(c)时采样半年图像 Fig.4 Theoretical values of gravity solid tides with different sampling rates for different periods at the same location |
为了不同的工作需求,设定不同采样率。若需精确知道1 s、1 min的重力固体潮理论值,可采用秒采样;若只需了解重力固体潮观测曲线的大致走向,可选择低频率采样,如时采样,将加大时间效率。
3 讨论为了验证计算结果的正确性,与郜晓亮等(2009)程序模拟结果作对比。采用相同的点位(104°E,30.6°N)数据,利用重力固体潮理论值计算程序,计算2008年11月1日至11日重力固体潮理论值。对比发现,2个计算结果在数值上吻合,且波峰和波谷的相位几乎一致,均接近郜晓亮等(2009)的计算结果,说明该程序比较可靠性。
采用重力固体潮理论值计算程序计算全球重力固体潮理论值,需模拟最大潮(农历腊月十五)和最小潮数据(农历腊月初七),观测半月潮变化。以2018年1月31日(农历腊月十五)和2018年1月23日(农历腊月初七)全球重力固体潮数据为例,对比最大潮和最小潮时的全球重力固体潮汐,结果见图 5,可见最大潮振幅明显比最小潮大,其中:最大潮正值最大值可达100 μGal左右,负值最大值可达-200 μGal左右;最小潮正值最大值可达70 μGal左右,负值最大值可达-120 μGal左右。
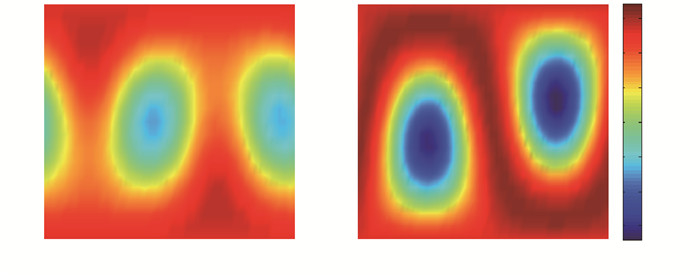
|
图 5 2018年1月23日与1月31日全球重力固体潮分布 (a)最小潮(农历腊月初七零时);(b)最大潮(农历腊月十五零时) Fig.5 Global gravity solid tide distribution on January 23 and January 31, 2018 |
由图 5可知,在南北纬20°附近,固体潮振幅出现最大值,与白赤交角和黄赤交角有关。黄赤交角是地球公转轨道所在的平面即黄道面与地球赤道面的交角,为23°26′。白赤交角是月球绕地球公转所在的平面即白道面与地球赤道面的夹角,最大值为28.5°,最小值为18.5°,变化周期18.6年。白赤交角和黄赤交角分别为地球距太阳和月亮的最近位置,由引潮力位计算公式[公式(1)、(3)]可知,距离越近,引潮力越大,从而导致振幅越大。
当太阳在赤道面时(春分3月21日—23日,秋分9月21日—23日),由于地球自转,地球赤道面同一地点的潮汐一天有2次高潮、2次低潮,此时潮汐产生EW向震荡。当太阳在南北回归线时(冬至12月22日—23日,夏至6月21日—22日),南北回归线的重力固体潮值达到最大值,此时潮汐不仅使地球产生EW向振荡,也会有NS向振荡。因此,每年5—7月(夏至前后)、11—12月(冬至前后),潮汐强度大(图 6),地震活动比较强烈。同理,月亮的赤纬角与黄赤交角也会使地球产生NS向震荡,周期则为每月2次。当太阳和月亮对地球的作用结合时,就会发生最强烈的潮汐NS向震荡。
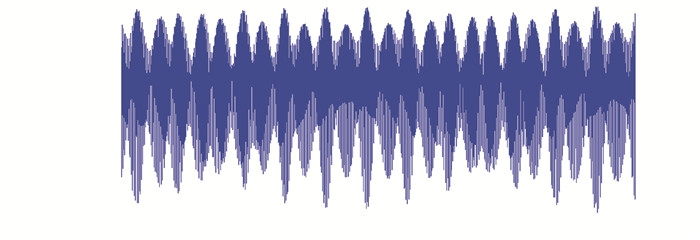
|
图 6 2017年整年重力固体潮理论值 Fig.6 The theoretical value of gravity earth tide for the whole year of 2017 |
此程序采用的起始计算时间指在GUI界面的“起始时刻”一栏输入的时间,得到未来24小时全球重力固体潮的动态模拟仿真。输出动画,由于文章的局限性,把每一帧图像截取出来,见图 7(图中经度以东经为正,纬度以北纬为正)。对比图 7中各时刻图像,清晰可见地球重力固体潮汐移动轨迹。

|
图 7 2017年1月1日1时至24时重力固体潮理论值全球仿真 Fig.7 Global simulation of theoretical values of gravity earth tide for the whole day of January 1, 2017 |
基于Matlab软件,利用其GUI开放环境,运用改进的新计算方法编写计算重力固体潮理论值的图形用户界面,通过与其他程序的重力固体潮理论值计算结果进行对比,验证了该程序的可靠性。通过观察全球重力固体潮理论值,发现在南北纬20°附近,振幅最大,应与白赤交角和黄赤交角有关,同时解释了在夏至和冬至前后地震活动强烈的原因。重力固体潮理论值计算程序实现了重力固体潮的可视化,为观察固体潮的分布规律提供了直观平台。
| 董良, 彭芳苹, 杨涛, 等. 利用新参数和软件改进重力固体潮计算程序[J]. 地球物理学进展, 2015, 30(1): 421-424. | |
| 樊华, 刘明军, 赵国春. 基于Matlab平台GUI的地震走时层析成像快速实现[J]. CT理论与应用研究, 2014, 23(3): 403-412. | |
| 方俊. 固体潮[M]. 北京: 科学出版社, 1984. | |
| 郜晓亮, 荆磊, 孙明国. 基于Matlab的重力固体潮理论值计算[J]. 中国西部科技, 2009, 8(1): 33-34. DOI:10.3969/j.issn.1671-6396.2009.01.017 | |
| 施晓红, 周佳. 精通GUI图形界面编程[M]. 北京: 北京大学出版社, 2003. | |
| 万永革, 黄猛. 固体潮汐理论值算法在VB6.0中的应用与实现[J]. 地震地磁观测与研究, 2006, 27(6): 97-102. DOI:10.3969/j.issn.1003-3246.2006.06.016 | |
| 王谦身. 重力学[M]. 北京: 地震出版社, 2003. | |
| 吴庆鹏. 重力学与固体潮[M]. 北京: 地震出版社, 1997. | |
| 郗钦文, 侯天航. 固体潮汐与引潮常数[J]. 中国地震, 1986, 2(2): 30-41. | |
| 徐华君, 柳林涛. 全球重力固体潮的可视化模拟[J]. 辽宁工程技术大学学报, 2006, 25(Z1): 76-78. | |
| 徐华君, 柳林涛, 罗孝文. 全球重力固体潮的仿真实现[J]. 系统仿真学报, 2009, 21(24): 7824-7827. | |
| 许厚泽, 张赤军. 我国大地重力学和固体潮研究进展[J]. 地球物理学报, 1997, 40(Z1): 192-205. DOI:10.3321/j.issn:0001-5733.1997.z1.017 | |
| 许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010. | |
| 张少泉. 有关地理纬度和地心纬度的换算问题[J]. 西北地震学报, 1985, 7(1): 41-45. | |
| 赵晓燕, 陈春生. 重力观测技术[M]. 北京: 地震出版社, 1997. | |
| 中国科学院地质研究所计算组. 固体潮理论值计算及其应用[J]. 地质科学, 1974, 9(3): 246-268. | |
| 中华人民共和国地质矿产部. DZ/T 0171-1997大比例尺重力勘查规范[S]. 1997. | |
| 朱平.固体潮汐对中国大陆地震活动性的影响研究[D].北京: 中国地震局地震研究所, 2005. |
 2019, Vol. 40
2019, Vol. 40

