地震动是由震源释放出来的地震波引起的地面运动,表征地震动的物理参数包括峰值、反应谱和持续时间等。地震动是由不同频率、不同幅值(或强度)在一个有限时间范围内的集合,通常以幅值、频率特性和持续时间3个参数表达地震特点(袁一凡等,2012)。地震动幅值是地震振动强度的表示,通常以峰值加速度、峰值速度来表示。地震动峰值大小反映了地震过程中某一时刻地震动的最大强度,直接反映了地震力及其产生的振动能量和引起的结构地震变形的大小,是地震对结构影响大小的尺度。地震动频谱特性是强震地面运动对具有不同自振周期结构的响应。反应谱是工程抗震用来表示地动频谱的一种特有方式,可以简单理解为具有相同阻尼特性,但结构周期不同的单自由度体系,在某一地震作用下的最大反应(袁一凡等,2012)。反应谱理论的提出和发展建立在强震动观测记录的基础之上。以往震害研究经验表明,近震、小震坚硬场地上的地震动所包含的高频震动比较丰富,容易和刚性结构产生共振响应后产生震害(张敏政,2015)。同理,对于远震、大震软厚场地上的地震动所包含的低频震动比较丰富,容易使高柔结构产生震害。强地震动的持续时间对结构的震害影响主要发生在结构反应进入非线性化之后,持时的增加使出现较大永久变形的概率提高,持时愈长,则反应愈大,产生震害的积累效应(周雍年,2011)。对一般工业民用建筑的抗震设计只考虑地震动幅值(强度)即可,但对重大结构和特殊工程的设计,还需加入持时对结构的特殊影响。
随着中国地震局“九五”数字化改造和“十五”数字地震网络项目的完成,我国已建成相当规模的强震动数字观测台网,近年已获取大量宝贵的近场数字化强震动观测记录,在工程抗震、大震应急、地震速报与预警和地震工程学的发展等方面,发挥了重要作用。国家强震动台网中心(国家地震科学数据共享中心强震动分中心)做为我国最权威的强震动观测记录提供单位,每年收到大量来自全国企事业单位和科研部门的强震数据申请需求(解全才等,2017)。伴随着强震动观测数据应用领域的不断扩展,数据共享的目标发展为根据用户需求提供定制化的数据服务,每条数据均可以严格、准确地反映所记录地点的震动情况,提高对原始二进制记录中能够反映传感器方向极性、记录触发时刻和转换因子等关键信息的解译。
作为国际上公认的优秀的数字信号处理程序,Matlab具有强大的计算功能和大量内置函数、可视化的编程界面、较高的编程效率,被广大爱好者所青睐,广泛应用于科学研究、工程计算和教学等方面。本文以Matlab语言为例,详细讲解如何在强震数据处理中识别并应用相关地震动特性参数。
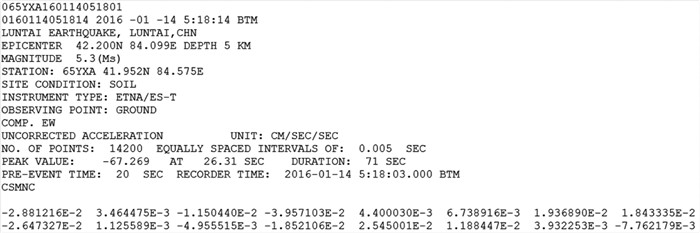
1 我国未校正加速度记录数据格式(UA)我国标准未校正强震动加速度记录由数据头段和数据区2部分组成,其中:数据头段为15行,主要由台站、地震和记录方向、数据峰值、触发时刻等信息组成;数据区为按行续写的的8列未校正的加速度数据(杨程等,2017)。数据头段信息详细解释见表 1,我国标准强震数据示例见图 1。
| 表 1 数据头段结构 Tab.1 The structure of data header |
|
图 1 我国标准强震数据示例 Fig.1 Example of standard strong motion data in China |
UA数据文件由数据头段和数据区2部分组成,在详细了解数据头段后,可以采用略过头段直接读取强震数据的方式,达到强震数据快速读取的目的。UA数据文件通常由3条数据代表一组加速度记录的3个方向(EW、NS、UD),在读取数据时可以一次读入,并把UA数据头段中相关重要信息,如台站代码、通道方向、峰值以及峰值时刻等参数,一并显示在波形振动图中。
2.1 零线漂移的消除理论上,即使无外界干扰,地球表面也在以一定频率发生着振动,即背景噪声一直存在。因此,地震后获取的加速度记录实际包含背景噪声干扰,导致加速度记录的初始值不为零。背景噪声与记录场地条件关系密切,体现为多种频率成分的随机波形(于海英等,2009)。所以,在架设强震仪时,根据中国数字地震观测网络技术规程中的要求,需要设置强震仪的事前时间为20 s,在一般基线校正过程中,采用减掉震前20 s数据的平均值或减掉整段时程均值的方法,去除记录的零线漂移趋势。Matlab中具体实现(文中出现的CH1为第1通道数据)代码如下
% CH1mean=mean(CH1(1:20* Samplefrequency)); “利用mean函数,计算前20 s数据的均值。
% CH1REMOVEZERO=CH1-CH1mean; “全部时程减去前20 s数据的均值”
使用该方法不会改变记录的形状,仅将时程进行上下平移。对数字强震仪而言,引起加速度记录零线漂移的因素除背景噪声外,还有传感器磁滞现象及仪器倾斜等。另外,在诸多文献中探讨的近断层强震记录基线漂移数据处理方法(于海英等,2009),需具体地震具体分析,文中主要介绍背景噪声引起的零线漂移去除方法。强震数据处理前需明确UA数据头段区的另一个重要参数“采样间隔”。通常,强震仪采样率设置为200 sps,即采样间隔为0.005 s,但随着“大监测”提出的关于测震强震一体化进程的开展,以及实时数据传输需要,越来越多的强震仪在架设时将采样率设置为100 sps。
2.2 加速度峰值及峰值时刻的计算地震动参数中的地震动幅值在强震记录中即加速度峰值、速度峰值。
(1) 计算最大峰值是指,在UA时程中,比较数据最大正值和最大负值的绝对值大小。确定最大正值或最大负值的过程在程序语言中是一种递推运算,在Matlab中可调用max函数或min函数一步完成,具体实现代码如下
% CH1maxpga=max(CH1result); “利用max函数找到第1通道全时程中的最大值”
% CH1minpga=min(CH1result); “利用min函数找到第1通道全时程中的最小值”
% if(abs(CH1maxpga) > abs(CH1minpga)); “最大值和最小值取绝对之后比较大小”
% CH1pga=CH1maxpga; “如果最大值的绝对值大,就把最大值赋值给第1通道做为峰值”
% else
% CH1pga=CH1minpga; “如果最小值的绝对值大,就把最小值赋值给第1通道做为峰值”
% end
(2) 确定峰值时刻是指,在UA时程中,找到与峰值对应的时刻。Matlab具体实现代码如下
% delta=1/Samplefrequency; “采样间隔”
% indexCH1=find(CH1result==CH1pga); “找到对应最大峰值的数组下标”
% indexCH1min=min(indexCH1); “选择最先到达的最大峰值数组下标”
% maxTCH1=indexCH1min*delta;
2.3 速度和位移的计算对未校正加速度数据做一次积分得到速度数据,再做一次积分得到位移数据。单纯的2次积分在处理近断层强震记录时并不理想,处理结果与GPS台站真实监测的永久位移数据并不相符,对此需具体分析,文中不做过多解释(于海英等,2009)。若加速度信号中有直流偏移量,通常可以在积分后做一次去趋势处理。使用Matlab的内置函数cumtrapz(基于梯形法则的数值积分公式)进行积分,输出一个与输入数据长度一致的数列。Matlab具体实现代码如下
% v=cumtrapz(t, CH1);“通过对加速度数据进行积分得到速度数据”
% zv=detrend(v); “通过detrend去趋势函数去除直流偏移量”
% d=cumtrapz(t, zv); “通过对速度数据进行积分得到位移数据”
% zd=detrend(d); “通过detrend去趋势函数去除直流偏移量”
2.4 加速度傅里叶幅值谱和反应谱的计算通常用来反映地震动频谱特性的谱有傅里叶谱、功率谱和反应谱。其中:①傅里叶谱包含傅里叶幅值谱和相位谱,全面描述地震动过程的频谱特征,包括各频率分量的相位及幅值信息,从2个傅里叶谱可以反推地震动时程;②功率谱为简化版的傅里叶谱,反映能量特性,失去相位信息;③反应谱一般指单自由度体系在地震时程作用下的最大响应,包括位移谱、速度谱和加速度谱,其作用是建立地震作用与结构特性之间的桥梁,实际工程设计中的振型分解反应谱法正是基于此。
2.4.1 加速度傅里叶幅值谱Matlab具体实现代码如下
% N=length(CH1);“计算CH1通道数据点数”
% fs=200;“采样频率”
% y1=fft(CH1, N); “通过fft函数做快速傅里叶变换”
% mag1=abs(y1)/fs; “求得傅里叶变换后的振幅值”
% ff1=(0:length(y1)-1)'*fs/length(y1);“幅值谱中频率序列”
% figure
% plot(ff1(1:N/2), mag1(1:N/2), 'k'); “画出在Nyquist频率之前随频率变化的振幅”
傅里叶幅值谱若在双数坐标系中显示,需使用“loglog”函数进行变换。
2.4.2 加速度反应谱反应谱以单质点系统振动为基础建立。通常可用卷积计算加速度反应谱,为了提高计算效率,采用逐步积分方法Newmark-β。该积分方法避免任何叠加应用,能较好适应非线性反应分析(金星等,2003)。
Newmark-β方法根据时间增量内假定的加速度变化规律,计算结构动力响应。由于时间增量内加速度变化规律的假定形式多样,通常只采用线性加速度和平均加速度。Newmark-β法统一表达式如下
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;{{\dot u}_{i + 1}} = {{\dot u}_i} + \frac{1}{2}\left({{{\ddot u}_{i + 1}} + {{\ddot u}_i}} \right)\Delta t\\ {u_{i + 1}} = {u_i} + {{\dot u}_i}\Delta t + \left({\frac{1}{2} - \beta } \right){{\ddot u}_i}\Delta {t^2} + \beta {{\ddot u}_{i + 1}}\Delta {t^2} \end{array} $ |
其中: β= 1/6为线性加速度,β= 1/4为平均加速度。可以证明,当β= 1/4,时加速度反应谱计算无条件收敛。
Newmark-β法计算步骤如下。
(1) 初始计算:①形成刚度矩阵[K]、质量矩阵[M]和阻尼矩阵[C];②给定初始值
(2) 对每个时间步的计算:①计算Δt+t时刻的有效荷载:
% newmark-beta method “从动态系统中获取反应谱数据”
% function [x, v, a]=newmarkb(M, K, C, N, P, x0, v0, a0, dt, RecordLength)“建立newmarkb函数”
% M:质量矩阵;K:刚度矩阵;C:阻尼矩阵;N:自由度:P:有效荷载;x0:初始位移向量;v0:初始速度向量;a0:初始加速度向量;dt:步长;RecordLength:采样点数;
%向量和矩阵的初始化
% x=zeros(N, RecordLength); %v=zeros(N, RecordLength); %a=zeros(N, RecordLength);
% P_ = zeros(N, RecordLength); %x(:, 1)=x0;v(:, 1)=v0;a(:, 1)=a0;
%计算前各类系数初始化
%deta=0.50;alpha=0.25;a0=1/alpha/dt^2;a1=deta/alpha/dt; a2=1/alpha/dt; a3=1/2/alpha-1;a4=deta/alpha-1;
% a5=dt*(deta/alpha-2)/2;a6=dt*(1-deta); a7=deta*dt;
% K_=K+a0*M+a1*C;
% iK=inv(K_);
% for i=1:RecordLength-1
% P_(:,i+1)=P(:,i+1)+M*(a0*x(:,i)+a2*v(:,i)+a3*a(:,i))+C*(a1*x(:,i)+a4*v(:,i)+a5*a(:,i));
% x(:,i+1)=iK*P_(:,i+1);
% a(:,i+1)=a0*(x(:,i+1)-x(:,i))-a2*v(:,i)-a3*a(:,i);
% v(:,i+1)=v(:,i)+a6*a(:,i)+a7*a(:,i+1);
% end
3 讨论我国是饱受地震灾害影响的国家之一,为了减轻地震造成的各种生命财产损失,必须了解地震动特性(强度、频谱以及持续时间等)及各类工程结构的地震反应特性。地震后的灾害调查除现场宏观震害调查外,快速的分析布设在各种工程结构、自由场地的强震动观测台站数据是最快捷、最准确的方法。
在“十五”数字观测网络项目中,中国地震局建成由1 390个自由地表固定台站、310个烈度速报台站、12个专业台阵和200台流动观测台站组成的强震动观测台网。截至2015年底,国家强震动台网中心共汇集、处理加速度记录31 360条,其中加速度大于10 Gal的强震动记录有12 005条。随着强震动观测数据的不断积累,每年有大量来自国内外高校、科研院所和企事业单位的数据申请需求。
随着强震动观测技术的不断发展,观测数据应用已不再局限于普通地震工程学领域,逐渐拓展到地震预警与烈度速报工程领域,为震后快速震害评估和应急方案制定提供基础数据,使得地震波到达前几秒到几十秒内对异地提供预警服务成为可能。
以我国标准强震动观测数据(UA)为例,针对一条标准的强震数据,基于Matlab程序,详细描述去漂移、计算峰值、速度和位移以及反应谱和傅里叶振幅谱的实现过程。该方法同样适用于国外多种格式的强震动观测数据分析处理。
| 解全才, 马强, 杨程. 强震动数据库发展现状与展望[J]. 地震工程与工程振动, 2017, 37(3): 48-56. | |
| 金星, 马强, 李山有. 四种计算地震反应数值方法的比较研究[J]. 地震工程与工程振动, 2003, 23(1): 18-30. DOI:10.3969/j.issn.1000-1301.2003.01.004 | |
| 杨程, 解全才, 马强, 王丽艳. 强震动记录数据格式研究[J]. 地震地磁观测与研究, 2017, 38(3): 196-202. DOI:10.3969/j.issn.1003-3246.2017.03.034 | |
| 于海英, 江汶乡, 解全才, 杨永强, 程翔, 杨剑. 近场数字强震仪记录误差分析与零线校正方法[J]. 地震工程与工程振动, 2009, 29(6): 1-12. | |
| 袁一凡, 田启文. 工程地震学[M]. 北京: 地震出版社, 2012: 7. | |
| 张敏政. 地震工程的概念和应用[M]. 北京: 地震出版社, 2015: 12. | |
| 周雍年. 强震动观测技术[M]. 北京: 地震出版社, 2011: 9. |
 2019, Vol. 40
2019, Vol. 40

