地震波传播过程中的能量衰减是地震研究的重要课题,对于地震波传播过程中的非弹性衰减,地震学上用品质因子Q值来加以度量。Q值是地球介质的一个重要基本参数,也是定量研究震源性质所必须的重要参数,也是地震学研究的重要组成部分,在震源物理、工程地震研究、地震预测预报中具有重要的应用价值。
现今,随着我国数字地震台网监测范围的日益扩大,数字地震记录资料的产出日益丰富。数字地震资料分析处理及各种地震参数的结果产出,是地震基础科研和地震预报的重要基础,体波Q值求解计算是其中一个重要方面。体波Q值的求解涉及大量数据处理运算,在以往区域体波Q值计算中,地震科研工作者一般选取某区域一段时间内大量地震记录数据,进行相应的位移谱求取、去噪处理,利用遗传算法进行最优化反演。计算过程较为复杂,每个步骤有不同处理方法,未集成较为方便、界面友好的软件进行地震体波Q值计算。
笔者以体波三段衰减模型为基础,在Matlab平台下开发地震体波Q值求解计算软件,在软件上实现体波Q值求解步骤,并在软件界面上设置对应的操作控件。软件界面友好,易于操作,最终可根据某批次地震记录产出地震发生区域的品质因子Q值。
1 体波Q值计算原理地震仪记录的地震波是一种综合信息,包含地震震源效应、地震波的传播路径效应、台站场地响应、仪器响应和噪声。地震记录在时间域的表达式为
| $ A_{i j}(t)=S_{i}(t) \otimes P_{i j}(t) \otimes L_{j}(t) \otimes I_{j}(t) \otimes N_{j}(t) $ | (1) |
式中,Aij(t)为第i个地震在第j个台站记录的地震记录位移(速度计或加速度型地震仪记录,可通过积分获得),Si(t)为震源效应,Pij(t)为传播路径效应,Lj(t)为台站场地响应,Ij(t)为仪器响应,Nj(t)为台站噪声。
将表达式(1)转换为频率域,卷积形式转换为乘积形式,则
| $ A_{i j}(f)=S_{i}(f) \cdot P_{i j}(f) \cdot L_{j}(f) \cdot I_{j}(f) \cdot N_{j}(f) $ | (2) |
式中,Pij(f)为与品质因子Q值相关的传播路径衰减项,有
| $ P_{i j}(f)=G\left(R_{i j}\right) \cdot \mathrm{e}^{\frac{\pi R_{i j} f}{Q(f) V}} $ | (3) |
去掉仪器响应Ij(f)和台站噪声Njj(f),式(3)转换为
| $ A_{i j}(f)=S_{i}(f) \cdot G\left(R_{i j}\right) \cdot \mathrm{e}^{\frac{\pi R_{i j} f}{Q(f) V}} \cdot L_{j}(f) $ | (4) |
根据Atkinson等(1992)的三段几何衰减函数经验公式,式中G(Rij)具体表述如下
| $ G\left(R_{i j}\right)=\left\{\begin{array}{ll}{R_{i j}^{-b_{1}}} & {R_{i j} \leqslant R_{1}} \\ {R_{1}^{-h} R_{1}^{b_{2}} R_{i j}^{-b_{2}}} & {R_{1} \leqslant R_{i j} \leqslant R_{2}} \\ {R_{1}^{-h} R_{1}^{b_{2}} R_{2}^{-b_{2}} R_{2}^{b_{3}} R_{i j}^{-b_{3}}} & {R_{i j} \geqslant R_{2}}\end{array}\right. $ | (5) |
式中:b1 = 1,b2 = 0.097,b3 = 0.5,R1 = 1.5H,R2 = 2.5H(H为区域地壳厚度),代入三段几何衰减模型,将等式两边取对数,可得
当Rij ≤ R1时
| $ \log A_{i j}(f)=\log S_{i}(f)-b_{1} \log R_{i j}+\frac{\pi R_{i j} f}{Q(f) V} \log \mathrm{e}+\log L_{j}(f) $ | (6) |
当R1 ≤ Rij ≤ R2时
| $ \log A_{i j}(f)=\log S_{i}(f)-b_{1} \log R_{01}-b_{2} \log \left(R_{i j} / R_{01}\right)+\frac{\pi R_{i j} f}{Q(f) V} \log \mathrm{e}+\log L_{j}(f) $ | (7) |
当Rij≥R2时
| $ \begin{aligned} \log A_{i j}(f)=& \log S_{i}(f)-b_{1} \log R_{01}-b_{2} \log \left(R_{02} / R_{01}\right)-\\ & b_{3} \log \left(R_{i j} / R_{01}\right)+\frac{\pi R_{i j} f}{Q(f) V} \log \mathrm{e}+\log L_{j}(f) \end{aligned} $ | (8) |
对于式(6)—式(8),未知量只有震源谱部分logSi(f)、非弹性衰减项πRijf/[Q(f)V]、场地响应项部分logLj(f),在地震记录足够情况下,联立方程组表现为超定方程形式,利用最小二乘法(王家映,2002)对一定批次的地震记录进行反演,反演不同频率点f下的πRijf/[Q(f)V],综合不同批次处理结果,拟合求取Q(f)与f对应关系,即可求得台站周围一定区域的品质因子值。另外,在地震体波Q值求解计算软件中采用非线性遗传算法反演方法,同样可求取不同频率点f下的πRijf/[Q(f)V],最终拟合求得Q(f)与f的对应关系。
2 数据处理根据三段几何衰减模型及最小二乘反演计算原理,软件总体设计思路如下:①导入原始地震波形数据; ②导入对应地震台站仪器参数数据; ③截取所分析地震S波时间长度,根据P波与S波走时差,经验估算S波持续时间,在软件内实现自动截取S波; ④根据P波与S波走时差,自动检索内嵌走时表确定震源距; ⑤依次计算S波位移谱并去仪器响应; ⑥对于不同的频率点f,采用最小二乘法,依次反演不同频率点下的品质因子Q。
2.1 数据导入sac数据格式为地震波形数据的通用格式,有ASCII码和二进制2种形式,广泛用于地震学分析软件。在JOPNES地震速报分析系统截取并导出sac地震记录数据文件与台站地震计参数的.par文件(包含对应地震记录的地震计灵敏度、传递函数零极点等信息)。将导出的地震记录和相关仪器参数信息的sac文件,导入地震体波Q值求解计算软件,在对应显示窗口直接显示地震记录和仪器幅频响应图。
2.2 地震S波位移谱求取S波位移谱求取是品质因子Q反演的基础,需要在软件中解决以下问题:①截取确定S波时间长度; ②去仪器响应; ③去背景噪声位移谱。
(1)确定S波时间长度。黄玉龙等(2003)指出,用于计算位移谱的S波时间长度应为从S波开始到包含90% S波能量的时间段,通过回归分析1 900条地震记录,得到S波截取时间长度与Pg、Sg波走时差为线性关系,并给出线性拟合表达式。采用黄玉龙等(2003)的研究结果,在地震体波Q值求解计算软件中,通过波形显示界面拾取Pg、Sg波走时差,确定S波位移谱计算时间长度。
(2)去地震计仪器响应。在地震体波Q值求解计算软件中,利用导入的仪器参数文件,计算仪器的幅频响应,求取地震S波记录速度震幅谱,在不同频率点上,将对应于该频率点的速度震幅谱除以相应仪器幅频响应值,完成去仪器响应,然后将速度震幅谱转换为位移震幅谱即可。
(3)去除背景噪声位移谱。在地震体波Q值求解计算软件中,选取Pg波或Pn波到时前256个点的时间记录段,计算其位移谱,然后在每个频点上,将对应的地震记录S波位移谱减掉噪声位移谱,得到去仪器响应与背景噪声后的纯地震S波位移谱。为了得到相同频率隔间点震幅谱,对于不同S波时间长度,软件采用平移窗谱法,得到S波地震位移谱后,插值求取以10为底的对数频率,即0.0、0.05、0.1、0.15、...、1.6,共33个频率点的位移谱,用于反演S波位移谱。
2.3 震源距计算以三段衰减模型为基础,推导得出,式(6)—式(8)中震源距Rij是反演求取品质因子Q值的必要参数。在地震体波Q值求解计算软件中,对于震源距采用以下算法处理:对于读入的地震记录,在界面上手动截取对应的Pg波与Sg波,利用二者走时差,根据所求地区走时表虚波速度,采用虚波速度法求取震源距(吴书贵等,2009)。
2.4 Q与频率f的反演拟合一般,在地震震幅谱求取准确、最小二乘反演偏差平方和最小或采用遗传算法收敛较好时,logQ与logf线性关系明显。但是,对于某些频率点,可能出现线性相关性较差的情况。对此,在地震体波Q值求解计算软件中,可以根据logQ与logf在双对数坐标系的显示情况,选取线性相关性好的点进行拟合,以期得到Q与f较好的拟合关系。
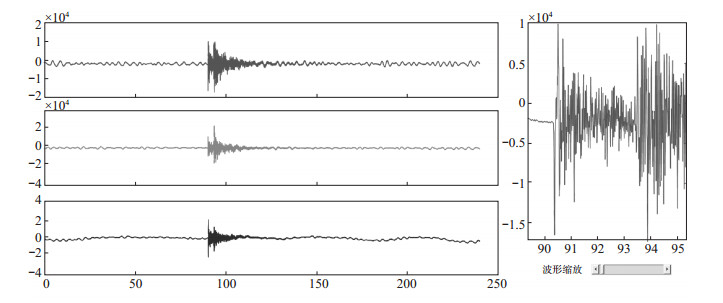
3 软件应用 3.1 软件界面地震体波Q值求解计算软件主界面包括参数输入及计算流程控制、波形显示、Q值结果拟合显示3部分,见图 1。运用界面上的滑动滚动条对波形数据进行缩放,将波形放大,手动拾取Pg与Sg波,以期求取较为准确的Pg与Sg波走时差,震相拾取见图 2。

|
图 1 程序界面截图 Fig.1 The surface of programme |
|
图 2 地震波形导入后放大波形细节截图 Fig.2 The magnified details of wave after importing seismic wave data |
软件计算流程由4个面板框控制,分别是区域波速度输入、地震数据及仪器参数读入、反演Q值最优化方式、拟合结果4个部分。
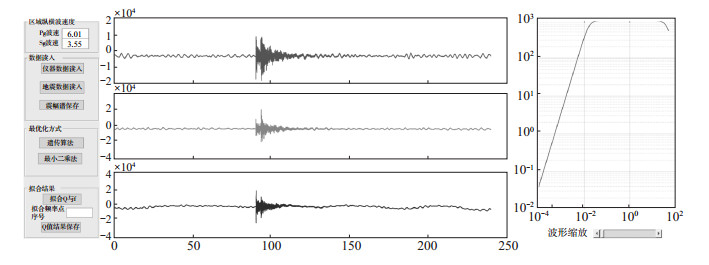
3.2 操作流程程序运行时,在面板框中输入本研究区域的Pg波及Sg波速度,然后逐条导入地震记录和对应的地震计仪器参数,计算该条地震记录位移震幅谱值的同时计算震源距。在面板中点击仪器数据读入,地震记录导入后,在左侧坐标轴中自动绘制该仪器的幅频响应,见图 3。
|
图 3 地震数据记录以及地震计幅频响应截图 Fig.3 The seismic wave data and amplitude frequency response of seismic instrument |
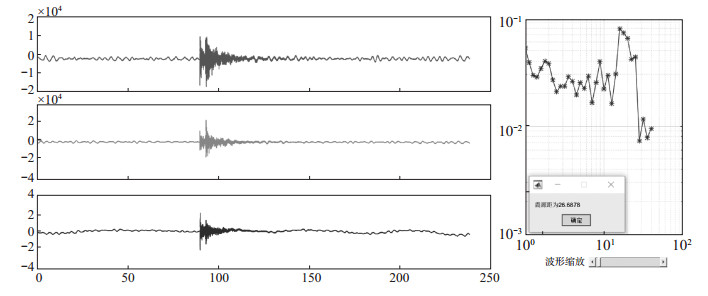
在中间坐标轴三通道地震记录里,选择某个通道,左侧窗口显示出来后,调节缩放波形,见图 2,拾取Pg、Sg波后,计算并显示该条记录位移谱及震源距,地震记录位移谱与震源距在软件界面左侧显示,见图 4。
|
图 4 地震数据记录以及地震记录位移谱截图 Fig.4 The seismic wave data and displacement spectrum |
计算需要分析的每条地震序列的震源谱与震源距,点击震源谱保存按钮,保存所有地震震源谱与震源距结果,点击最优化方式中的最小二乘法或遗传算法按钮,读取保存的震源谱与震源距结果,反演计算每个频点f的Q值,然后进行拟合,得到Q与f的拟合关系。
3.3 应用实例以广东地震台网记录的2017年5月23日21时39分广东阳江ML 2.9地震为例,验证地震体波Q值求解计算软件的实用性。广东地震台网大部分台站及部分省外台站清晰记录到此次地震波形,将地震记录及仪器参数逐条导入软件,计算各条地震位移震幅谱,选取最小二乘法或遗传算法进行反演,每个频点f与对应的Q结果采用双对数坐标系显示在软件界面左侧,中间第3个坐标轴显示用于计算的所有震源谱,可见约10 Hz以上频点线性关系较好,选取10 Hz以上频率点开始的拟合结果,见图 5,得到由该批次地震序列计算得到的品质因子Q与f的关系式:Q(f) = 469.62f 0.4467。

|
图 5 Q与频率f的拟合关系截图 Fig.5 The fitting relationship between Q value and frequency f |
为了验证该软件对Q反演结果的准确性,选择广东河源新丰江水库区域2017年2月28日ML 3.6地震进行计算,Q(f)拟合结果见图 6,得到由该地震序列品质因子Q与f的关系式:Q(f) = 399.80f 0.38823。

|
图 6 2017年2月28日ML 3.6地震 Q(f)拟合结果 Fig.6 The Q fitting result of the ML 3.6 earthquake on Feb.28, 2017 |
对比分析可知,2次不同区域地震的反演计算结果与黄玉龙等(2003)反演所得广东地区体波Q值平均结果Q(f) =(481.5±73.28)f 0.31基本相当。新丰江水库地区比阳江地区Q值结果小,说明新丰江地区地震活动性较强,与每年广东地区地震编目结果显示的新丰江区域地震频度高于阳江地区是一致的,从侧面佐证了结果的准确性。
5 结束语以Matlab为开发平台,编制基于三段衰减模型的S体波品质因子Q值计算软件,并通过相关震例的计算,对比前人Q值计算结果,证明了利用该软件所得Q值计算结果的准确性。该软件界面友好,将数据导入、仪器响应去除、最优化反演、结果拟合集成一体,操作简单,可用于某个区域范围内Q值计算、大震前后Q值追踪变化研究等工作。体波Q值的计算过程,可满足不同层次地震工作人员的研究工作,值得推广。
| 黄玉龙, 郑斯华, 刘杰, 等. 广东地区地震动衰减和场地响应的研究[J]. 地球物理学报, 2003, 46(1): 54-61. DOI:10.3321/j.issn:0001-5733.2003.01.009 | |
| 王家映. 地球物理反演理论[M]. 北京: 高等教育出版社, 2002: 18-38. | |
| 吴书贵, 赵永. 实用数字地震分析[M]. 北京: 地震出版社, 2009: 113-115. | |
| Atkinson G, Mereu R. The shape of ground motion attenuation curves in southeastern Canada[J]. Bull Seismol Soc Am, 1992, 82(5): 2014-2031. |
 2019, Vol. 40
2019, Vol. 40

