2. 中国石家庄 050021 河北省地震局
2. Hebei Earthquake Agency, Shijiazhuang 050021, China
大地震除产生涉及地球局部运动的体波和面波外,还能激发全球规模的地球自由振荡。1960年,贝尼奥夫小组(Benioff et al,1961)和Ness等(Ness et al,1961)分别用Isabella应变仪和Lacoste-Romberg重力仪观测到智利8.9级大地震激发的地球自由振荡,从而拉开了一个新的地球物理学分支的序幕。
21世纪以来,地球自由振荡研究在中国受到广泛关注,其中一个重要的研究方向是,对地球自由振荡谱峰之频率的研究与检测,如:雷湘鄂等(2002)利用超导重力观测资料研究2001年秘鲁大地震激发的地球自由振荡; 万永革等(2007)利用中国数字地震台网观测资料、邱泽华等(2007)利用钻孔差应变仪观测资料、唐磊等(2007)利用中国钻孔体应变台网观测资料、任佳等(2009)利用数字水位观测资料,研究2004年苏门答腊大地震激发的地球自由振荡; 孟方杰等(2018)利用中国大陆倾斜台网多台垂直摆倾斜仪数据,研究2011年日本大地震激发的低频自由振荡。目前,利用数字化形变观测资料仅能检测到频率小于0S60振型的基频球型自由振荡,而利用分钟值采样数据,理论上应能检测到0S2—0S76的基频球型振荡。如何进一步提取更高频率的地球球型自由振荡,是当前广大科研工作者关注的问题。
利用地球自由振荡观测资料,不仅可以约束地球内部结构(Dziewonski et al,1981),还可以反推震源破裂参数,并对地球液体层和固体层之间的相互作用提供约束(Park et al,2005)及研究慢地震和静地震等(Beroza et al,1990)。因此,进行范围更广的地球自由振荡振型的检测具有重要意义。2011年3月11日在日本东北部海域发生9.0级地震,引发海啸和核泄露,造成重大人员伤亡和财产损失。文中利用张家口地震台体应变观测资料,采用功率谱密度估计方法,研究此次9.0级大地震激发的地球球型自由振荡。
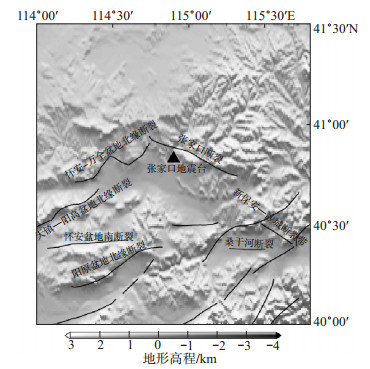
1 观测背景张家口地震台(下文简称张家口台)地处阴山EW向构造带与山西地震带北段、张渤地震带西北段交汇部位,附近主要断裂有张家口断裂、怀安—万全盆地北缘断裂、天镇—阳高盆地北缘断裂、怀安盆地南断裂、阳原盆地北缘断裂、桑干河断裂和新保安沙城断裂,见图 1。
|
图 1 张家口地震台地质构造位置 Fig.1 Tectonic positions at Zhangjiakou Seismic Station |
张家口台形变观测井位于张家口市桥东区鱼儿山山脚,井孔岩性为侏罗纪火山岩,钻孔直径220 mm,孔深63.2 m,井水为基岩裂隙水,与地表潜水不相通,水温约11 ℃,1989年5月安装TJ-1型钻孔体应变仪(由中国地震局地壳应力研究院研制,是目前我国应变潮汐观测台网中使用的主要观测仪器,下文简称体应变仪),探头埋深约20 m,灵敏系数为14.73 mV/10-8,年稳定性4.0×10-8(池海江等,2005)。自安装以来,TJ-1型钻孔体应变仪工作状态良好,体应变观测资料稳定、可靠,适合观测地球球型自由振荡。
2 体应变观测资料预处理2011年3月11日日本9.0级地震发生后,张家口台体应变观测记录到地震异常数据。分析发现,3月11日—15日(7 200 min)震后影响比较明显,分钟值原始曲线见图 2。由图 2可见,数据虽未经干扰剔除处理,但固体潮和地震波清晰可见。

|
图 2 张家口地震台TJ-1型钻孔体应变仪记录的日本9.0级大地震分钟值曲线 Fig.2 Minute value curve of the Japan M 9.0 earthquake recorded by TJ-1 the borehole strainmeter at Zhangjiakou Seismic Station |
地球自由振荡信号属于非稳态信号(瞬态信号),通常采用功率谱密度估计方法进行分析。功率谱密度的谱分辨率与数据长度成正比,若采样数据过少,则不能有效分辨其频率成分。因此,应保证数据样本有足够长度,频谱图才具有较高质量。
地震发生后,激发的地球自由振荡振幅随着时间流逝快速衰减。样本数据多,会对高频自由振荡信号产生抑制效应,若样本数据少,则不能有效识别低频自由振荡信号。在保证低频自由振荡信号的分辨率,又不对高频自由振荡信号产生抑制效应的前提下,选取此次9.0级地震发生后,张家口体应变记录的震后影响明显的分钟值观测数据,即3月11日—15日共7 200个数据进行预处理,剔除错误数据(如尖蜂、突跳、掉格等),基于潮汐模拟信号,对因断电、地震等导致中断的数据进行内插,采取逐步增减数据个数的方法进行试验,解决数据长度与地球自由振荡信号衰减之间的矛盾,提取此次9.0级地震激发的地球球型自由振荡振型。试验结果表明,对于此次9.0级地震,采用震后1 400—2 000个数据进行分析较为合理。
3 地球自由振荡谱分析数据预处理后,采用功率谱密度估计方法分析地球自由振荡信号。
3.1 计算原理功率谱密度估计定义为记录到波形资料的自相关函数Rn的傅里叶变换(万永革,2007),即
| $ {S_k} = \sum\limits_{n = 0}^{N - 1} {{R_n}} {{\rm{e}}^{ - i\frac{{2\pi nk}}{N}}}\quad k = 0, \quad 1, 2, \ldots, N - 1 $ | (1) |
| $ R_{n}=\frac{1}{N} \sum\limits_{j=0}^{N-1} x_{j} x_{j+n} \quad n=-(N-2), -(N-1), \cdots, -1, 0, 1, \cdots, N-2, N-1 $ | (2) |
式中,Sk为功率谱密度离散值,其所对应的频率值由观测数据采样率(60/s)乘以k确定; N = 2 000,为参与计算的数据个数; x为张家口台记录的体应变数据; k为序号。
为消除数据不能无限长而必须加窗对功率谱密度估计的影响,采用汉宁窗来抑制旁瓣,以突出主瓣。
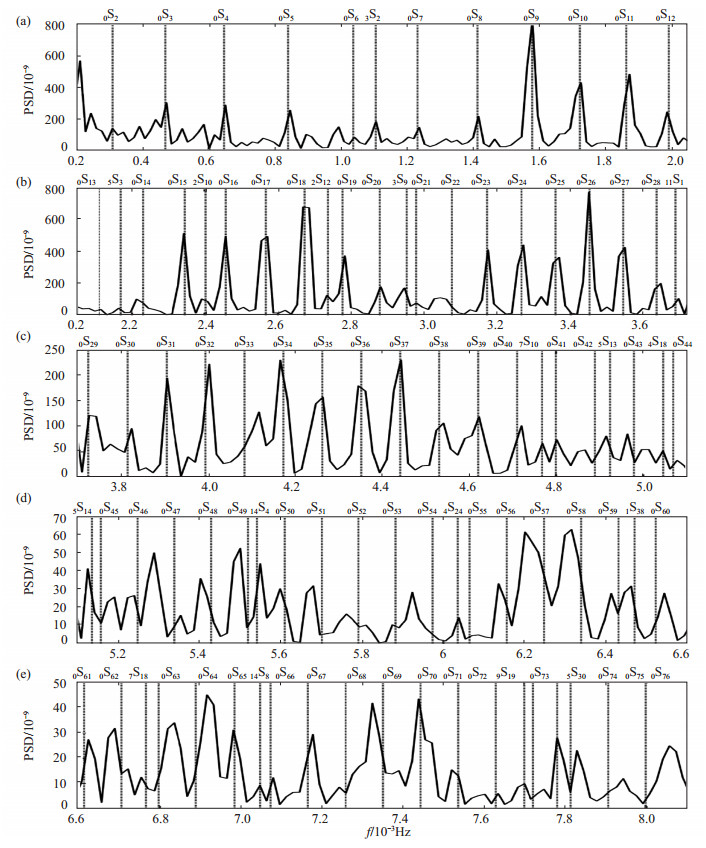
3.2 功率谱密度估计据以上功率谱计算方法,计算0.2 mHz—8.1 mHz频率范围内张家口台体应变观测数据功率谱密度,分析不同频段功率谱密度(相对值)与PREM模型的球型振荡频率的对应关系。体应变数据功率谱密度(PSD)估计结果见图 3,图中虚线表示地球初步参考模型(PREM模型)给出的球型自由振荡理论频率值。
|
图 3 0.2 mHz—8.1 mHz频段体应变数据功率谱密度估计曲线 (a) 0.2 mHz—2.05 mHz频段; (b)2.05 mHz—3.7 mHz频段; (c)3.7 mHz—5.1 mHz频段; (d) 5.1 mHz—6.6 mHz频段; (e)6.6 mHz—8.1 mHz频段 Fig.3 Curve of power spectral density estimation of the volume strain data in the frequency scope from 0.2 mHz to 8.1 mHz |
(1)0.2 mHz—2.05 mHz频段。清晰检测到球型振荡的基频振型0S2—0S12和谐频振型3S2。
(2)2.05 mHz—3.7 mHz频段。0S13和0S22振型观测效果不明显,不能清晰分辨其突出的谱峰,可准确检测到其他基频振型,仅0S14振型观测频率值与PREM模型理论值偏差较大。此外,准确检测到谐频振型5S3、2S10、2S12、3S9、11S1。
(3)3.7 mHz—5.1 mHz频段。检测到基频球型自由振荡0S29—0S44和谐频球型自由振荡7S10、5S13、4S18。其中:0S42振型观测效果不明显,0S33和0S43振型观测频率值偏离PREM理论值较大,其余振型符合较好。
(4)5.1 mHz—6.6 mHz频段。检测到基频球型自由振荡0S45—0S60和谐频球型自由振荡5S14、14S4、4S24、1S38。其中:0S52、0S53、0S54、0S55、0S57振型观测效果不明显,其余振型可较准确地检测到,0S45、0S48、0S49、0S51振型观测频率值与PREM模型理论值偏差较大。
(5)6.6 mHz—8.1 mHz频段。检测到基频球型自由振荡0S61—0S76和谐频球型自由振荡7S18、14S8、9S19、5S30。其中:0S68、0S73、0S75、0S76振型观测效果不明显,其他振型可较准确地观测到,0S63、0S64、0S69观测频率值偏离PREM理论值较大。
根据功率谱密度估计结果,统计张家口台体应变仪检测到的日本9.0级大地震激发的球型自由振荡观测周期,并与PREM模型理论值进行对比,结果见表 1,可知:0S2、3S2、0S9、0S16、0S21、0S23、0S26、0S27、0S31、0S35、0S37、0S39、7S10、0S41、4S18、4S24、0S65、14S8、0S70、0S72、9S19、5S30共22个振型的观测周期,与理论值偏差均小于0.1%;0S13、0S22、0S42、0S52、0S53、0S54、0S55、0S57、0S68、0S73、0S75、0S76共12个振型,与附近噪声无法区分,未形成突出的谱峰,观测效果不明显。由表 1可见,绝大部分振型的观测周期与理论值偏差在0.5%以内,说明对0S2—0S74基频和17个谐频球型自由振荡的检测结果,与PREM模型的理论值基本一致,表明张家口台体应变仪对地球自由振荡的检测比较成功。
| 表 1 观测周期与PREM模型理论周期对比 Tab.1 The contrast between the observation period and the theoretical period of PREM model |
选取张家口台体应变仪观测资料,对日本9.0级大地震激发的地球自由振荡进行提取, 准确检测到基频球型振荡0S2—0S74和17个谐频球型振荡3S2、5S3、2S10、2S12、3S9、11S1、7S10、5S13、4S18、5S14、14S4、4S24、1S38、7S18、14S8、9S19、5S30,并与地球初步参考模型(PREM)的理论自由振荡周期进行对比,发现实测振荡周期与PREM预测的振荡周期基本一致,说明该台体应变仪运行状态良好,对地球自由振荡的检测比较成功,表明文中给出的研究结果比较可靠。
在保证低频自由振荡信号的分辨率,又不对高频自由振荡信号产生抑制效应的前提下,采用功率谱密度估计方法直接提取地球自由振荡信息,研究结果证明该方法可行,为检测球型自由振荡提供了一种切实可行的研究方法。
高频(4.8 mHz—8.1 mHz)部分的自由振荡相对幅度低于低频(0.2 mHz—1.5 mHz)和中频(1.5 mHz—4.8 mHz)部分,可能是因为高频部分不易被准确检测到。在5.1 mHz—8.1 mHz的某些高频频段附近存在另外一些谱峰峰值,与PREM模型理论计算值偏差较大, 可能与地球介质的横向不均匀性或各向异性有关,具体原因有待进一步研究。
PREM模型数据由万永革老师提供,在此表示感谢。| 池海江, 朱振兴, 王锐锋, 等. 张家口台印尼苏门答腊大地震钻孔应变观测报告[J]. 地壳构造与地壳应力, 2005(2): 4-8. | |
| 雷湘鄂, 许厚泽, 孙和平. 利用超导重力观测资料检测地球自由振荡[J]. 科学通报, 2002, 47(18): 1432-1436. | |
| 孟方杰, 张燕, 赵佳佳. 利用全台网垂直摆倾斜仪数据检测日本MW 9.0地震激发的低频自由振荡[J]. 大地测量与地球动力学, 2018, 38(6): 650-654. | |
| 邱泽华, 马瑾, 池顺良, 等. 钻孔差应变仪观测的苏门答腊大地震激发的地球环型自由振荡[J]. 地球物理学报, 2007, 50(3): 797-805. DOI:10.3321/j.issn:0001-5733.2007.03.019 | |
| 任佳, 陈华静, 蒋翠荣, 等. 数字化水位仪观测的苏门答腊大地震激发的地球球型自由振荡[J]. 地震研究, 2009, 32(4): 333-338. DOI:10.3969/j.issn.1000-0666.2009.04.002 | |
| 唐磊, 邱泽华, 阚宝祥. 中国钻孔体应变台网观测到的地球球型振荡[J]. 大地测量与地球动力学, 2007, 27(6): 37-44. | |
| 万永革, 盛书中, 周公威, 等. 中国数字地震台网记录的苏门答腊-安达曼地震激发的地球球型自由振荡的检测[J]. 地震学报, 2007, 29(4): 369-381. DOI:10.3321/j.issn:0253-3782.2007.04.004 | |
| 万永革. 数字信号处理的MATLAB实现[M]. 北京: 科学出版社, 2007. | |
| Benioff H, Press F, Smith S. Excitation of the free oscillations of the Earth by earthquakes[J]. J Geophys Res, 1961, 66(2): 605-619. DOI:10.1029/JZ066i002p00605 | |
| Beroza G C, Jordan T H. Searching for slow and silent earthquakes using free oscillations[J]. J Geophys Res, 1990, 95(B3): 2485-2510. DOI:10.1029/JB095iB03p02485 | |
| Dziewonski A M, Anderson D L. Preliminary reference earth model[J]. Phys Earth Planet Inter, 1981, 25(4): 297-356. DOI:10.1016/0031-9201(81)90046-7 | |
| Ness N R, Harrison C T, Slichter L B. Observations of the free oscillations of the earth[J]. J Geophys Res, 1961, 66(2): 621-629. DOI:10.1029/JZ066i002p00621 | |
| Park J, Song T R A, Tromp J, et al. Earth's free oscillations excited by the 26 December 2004 Sumatra-Andaman earthquake[J]. Science, 2005, 308(5725): 1139-1144. DOI:10.1126/science.1112305 |
 2019, Vol. 40
2019, Vol. 40


