2. 中国北京 100081 中国地震局地球物理研究所;
3. 中国济南 250014 山东省地震局
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China;
3. Shandong Earthquake Agency, Jinan 250014, China
地震后地球自身产生的振动称为自由振荡。大地震所产生的地球自由振荡可以延续数周, 甚至数月。对地球自由振荡的认识是地球科学的重要发现之一(傅承义等, 1985)。19世纪末期, Lamb(1882)从理论上推导, 均匀球体简单模型下的自由振荡包括球型振荡和环型振荡2种振型; 1911年, Love(1912)在Lamb(1882)的研究基础上, 考虑了重力作用下可压缩球体振荡问题; 1954年, Benioff等(1961)发现, 应变仪记录到1952年11月4日堪察加地震产生的长周期地震波; 1960年5月22日智利大地震后, Benioff等(1961)、Ness等(1961)、Alsop等(1961)分别观测到该地震激发的地球自由振荡, 为地震学开创了一个全新领域。
地球的自由振荡分为球型振荡S和环型振荡T。球型振荡质点位移包含同心球面水平分量, 同时包含球体径向分量, 而环形振荡质点位移仅有同心球面水平分量。因此, 理论上, 重力仪、地震仪垂向分量、GPS阵列的垂向分量等只能记录到球型振荡信号, 而应变仪、倾斜仪、地震仪水平分量、GPS阵列的水平分量可以同时记录到球型振荡和环形振荡。实际上, 地球物理学结构横向不均匀性及径向不均匀性、地球自转、地球椭率、地球内部各向异性、非弹性以及震源机制性质, 共同造成环型振荡, 产生垂直分量运动, 所以重力仪、地震仪垂向分量等也能记录到环型振荡(Dziewonski et al, 1972;吕永清等, 1997;雷湘鄂等, 2002, 2004, 2007;万永革等, 2004, 2005, 2007;Rosat et al, 2005;于海英等, 2006;邱泽华等, 2007;Mitsui et al, 2012;栾威等, 2015)。
研究地球的自由振荡, 对了解地球密度和弹性结构、地球的非完全弹性以及地震的震源机制等具有重要作用。地球产生的不同自由振荡模态与地球内部相关物理参数有关, 通过观测地球自由振荡模态, 可反过来约束地球内部相关物理参数, 不同震源机制激发的地球自由振荡具有不同波谱结构和振荡特征, 其物理本质及确切的形成机理有待进一步研究。
JCZ-1T超宽频带地震计的LP通道为360 s-DC的加速度平坦输出, 能够记录大于360 s的地震长周期信号, 也能够记录月亮等天体与地球相对运动引起的重力固体潮汐以及地球的自由振荡(蔡亚先等, 2007)。对于BB通道(对速度输入响应平坦), 响应在3 600 s已衰减到-40 dB, 即0.01, 对周期大于6 min的带外信号不敏感; 对于LP通道(对加速度输入响应平坦), 响应在100 s时衰减到约-20 dB, 即0.1, 对周期大于6 min的信号敏感, 也能记录到周期约100 s的信号, 只是信号幅度衰减, 约为360 s-DC通带信号幅度的1/10。文中采用泰安基准地震台(下文简称泰安台)JCZ-1T地震计LP通道数据, 检测斐济MW 8.2深震(震源深度600 km)激发的地球自由振荡, 检测到球型振荡的零级、基振型和高振型以及环形振荡的基振型和高振型, 并分析球型和环型振荡之间的耦合效应。
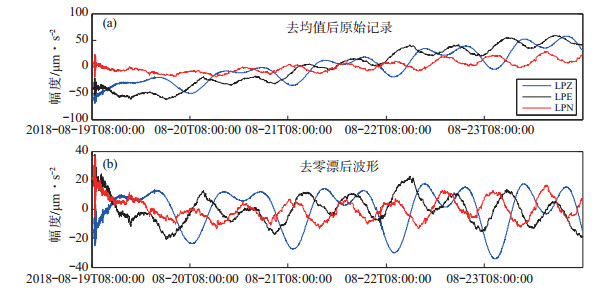
1 数据预处理北京时间2018年8月19日08时19分40秒, 斐济发生MW 8.2地震, 震中位于(18.178°S, 178.111°W), 震源深度600.0 km。采用泰安台JCZ-1T地震计LP通道2018年8月19日08时至24日08时共计120小时数据记录, 检测该地震激发的自由振荡。将所选地震波形去除仪器响应并去均值后, 进行去零漂处理, 结果见图 1[横坐标为时间轴(北京时), 纵坐标为加速度幅值, 单位μm/s2; 蓝色曲线为UD分量数据(LPZ), 黑色曲线为EW分量数据(LPE), 红色曲线为NS分量数据(LPN)]。由图 1(b)可知, 斐济地震激发的地震波清晰可见, 且LPZ分量固体潮记录清晰。
|
图 1 泰安台JCZ-1T超宽频带地震计120小时波形曲线 (a)去除仪器响应及去均值后的原始记录波形; (b)图 1(a)中数据去零漂处理后波形曲线 Fig.1 120 hours length waveform of JCZ-1T ultra broadband seismometer of Taian Seismic Station |
采用经典的谱分析方法(Welch方法), 计算单边功率谱密度, 使用Hamming窗抑制旁瓣, 突出主瓣, 并得到非负功率谱密度。将数据分为8段, 每段重叠50%, 分别计算每段功率谱密度, 之后进行叠加, 得到平均周期图谱。计算公式为
| $ P\left(\omega \right) = \frac{1}{L}\sum\limits_{i = 1}^L {} {P^i}\left(\omega \right) = \frac{1}{L}\sum\limits_{i = 1}^L {} \left({\frac{1}{N}|\sum\limits_{n = 0}^{N - 1} {x_N^i\left(n \right){e^{ - j\omega n}}} {|^2}} \right) $ | (1) |
式中, L为分段数量, N为Hamming窗长度, xNi (n)为第i分段数据。
该方法简单, 且稳定有效, 能够清晰表现数据的频谱。
2.2 功率谱密度估计对于均匀且各项同性球体, 垂直分量仅能够记录到球型振荡, 水平分量可以同时记录到球型振荡和环形振荡, 但实际上, 由于地球介质不均匀性和各向异性导致垂直分量能够记录到环形振荡分量, 利用式(1), 计算泰安台JCZ-1T超宽频带地震计3个LP分量0.001-0.01 Hz频带范围内的功率谱密度, 并将PREM模型球型振荡和环形振荡共计171个振型的理论值一并绘制在图中, 删除LP分量无明显特征的振型理论值, 得到3个LP分量的功率谱密度估计曲线, 与地球初步参考模型(PREM)的理论自由振荡周期进行对比, 结果见图 2-图 7。
|
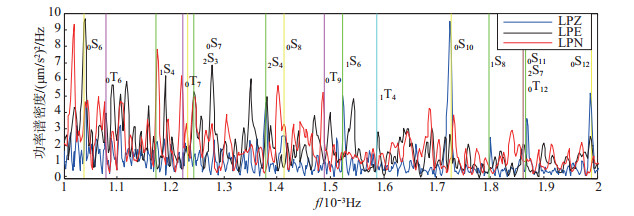
图 2 0.001—0.002 Hz频段3个LP分量功率谱密度估计 Fig.2 Power spectral density estimation of three LP component from 0.001 to 0.002 Hz |
|
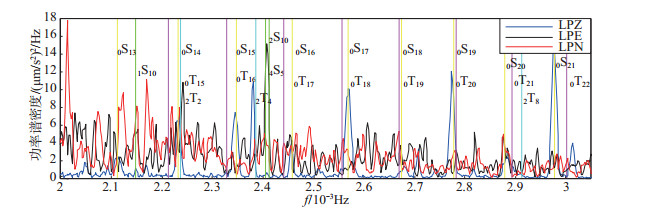
图 3 0.002—0.003 Hz频段3个LP分量功率谱密度估计 Fig.3 Power spectral density estimation of three LP component from 0.002 to 0.003 Hz |
|
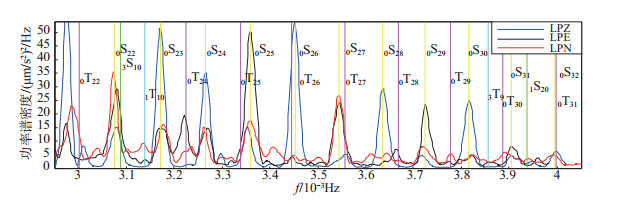
图 4 0.003—0.004 Hz频段3个LP分量功率谱密度估计 Fig.4 Power spectral density estimation of three LP component from 0.003 to 0.004 Hz |
|
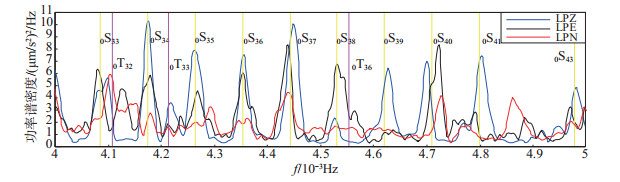
图 5 0.004—0.005 Hz频段3个LP分量功率谱密度估计 Fig.5 Power spectral density estimation of three LP component from 0.004 to 0.005 Hz |
|
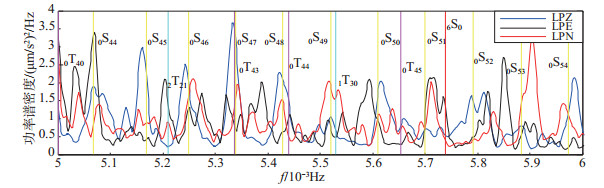
图 6 0.005—0.006 Hz频段3个LP分量功率谱密度估计 Fig.6 Power spectral density estimation of three LP component from 0.005 to 0.006 Hz |
|
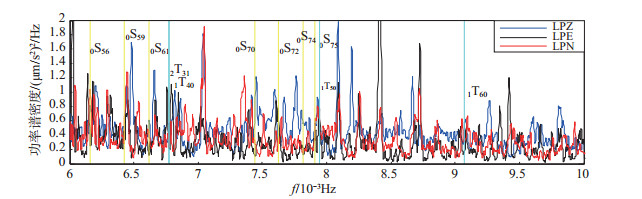
图 7 0.006—0.01 Hz频段3个LP分量功率谱密度估计 Fig.7 Power spectral density estimation of three LP component from 0.006 to 0.01 Hz |
图 2-图 7中竖线表示PREM模型自由振荡振型的理论值, 其中:球型振荡的零级振型为红色竖线, 基振型为黄色竖线, 高振型为绿色竖线; 环形振荡的基振型为洋红色竖线, 高振型为青绿色竖线。
由LP分量功率谱密度估计曲线可知, 低于0.001 Hz频段无明显振型特征, 在0.002—0.006 Hz频段, 可观测到丰富的自由振荡振型, 且振幅均相对明显, 低于0.002 Hz、高于0.006 Hz频段, 3个LP分量功率谱密度振幅明显变小, 振型检测难度和模糊度增加。由图 2可见, 在0.001—0.002 Hz频段, 记录到零级球型振荡以及基振型和高振型球型振荡和环形振荡, 其中:0S11、2S7和0T12振型几乎重叠, 无法分辨; 0S7、0T7间距较小。由图 3可见, 0S14—0S21和0T15—0T22振型间距较小, 尤其是0S19和0T20振型几乎重叠, 难以分辨。由图 4可见, 0S26和0T26振型间距较小, 最大振幅频点观测值介于二者之间, 认为是二者耦合所致。由图 2—图 7可见, 球型振荡在垂直分量表现明显, 即图中LPZ分量功率谱密度曲线(蓝色线条)在PREM模型球型振荡振型理论值位置附近振幅较大, 而2个水平分量功率谱密度曲线(黑色和红色线条)在PREM模型环型振荡振型理论值附近位置振幅相对较大, 即垂直分量记录球型震荡更加清晰, 水平分量记录环型震荡更加清晰, 与之前所述“理论上垂直分量仅能够记录到球型振荡, 水平分量可以同时记录到球型振荡和环形振荡”的结论相符。图 4中0S32和0T31振型几乎重叠, 基于上述分析, 认为由LPZ分量检测到球型震荡0S32振型, 由LPE和LPN分量检测到环型震荡0T31振型。图 7中的1T40和2T31振型几乎重叠, 无法分辨。
3 结论与讨论利用泰安台JCZ-1T地震计LP通道120小时数据记录, 获得2018年8月19日斐济MW 8.2地震激发的地球自由振荡, 检测到基频球型振荡0S6—0S58几乎所有振型, 同时检测到球型振荡的部分零级振型和高振型以及环形振荡的部分基振型和高振型。
(1) 使用PREM模型球型振荡和环形振荡共计171个振型的理论值, 对JCZ-1T超宽频带地震计3个LP分量的功率谱密度进行检测, 共检测到68个与模型比对一致的清晰振型, 由于PREM理论值接近, 有7个振型无法准确判定, 即为:图 2中的0S11、2S7和0T12振型, 图 3中的0S14和2T2振型, 图 7中的1T40和2T31振型。
(2) 对3个LP分量功率谱密度进行振型检测, 根据自由振荡原理以及相关研究成果(于海英等, 2006;邱泽华等, 2007;万永革等, 2007;栾威等, 2015), 对于球型振荡与环形振荡振型差异较小甚至几乎重叠的现象, 如图 3中0S14—0S21和0T15—0T22, 认为球型振荡在LPZ分量表现明显, 环形振荡在LPE和LPN分量表现明显。
(3) 球型振荡基振型在(2—3)×10-3Hz、(3—4)×10-3Hz、(4—5)×10-3Hz及(5—6)×10-3Hz频段分别表现出不同特征, 即在(2—3)×10-3Hz频段, 奇数振型振幅(如0S13、0S15、0S17)明显大于偶数振型振幅(如0S14、0S16、0S18), 而(3—4)×10-3Hz频段则相反, 即球型振荡基振型的偶数振型振幅大于奇数振型振幅, (4—5)×10-3Hz频段反之, 如此循环往复。
(4) 观测到多个振型频点耦合现象, 即最大观测值对应频点位于2个理论振型频点之间, 此最大值应为2个理论振型耦合所致。如4S5和2S10、0T26和0S26振型, 对于振型耦合, 一般以2个理论振型频点之差为判定依据, 当差值大于2.3×10-7Hz时, 则为“真实耦合”, 否则为“虚假耦合”。
(5) 振荡周期观测值与PREM理论值基本一致, 部分存在微小差值, 认为由地球介质的横向不均匀性和各向异性所致。因此, 可以通过地球自由振荡结果约束地球横向不均匀性或各向异性。
| 蔡亚先, 吕永清, 程骏玲, 等. JCZ-1T超宽频带地震计作为综合观测仪器的拓展应用[J]. 地震地磁观测与研究, 2007, 28(5): 29-34. DOI:10.3969/j.issn.1003-3246.2007.05.009 | |
| 傅承义, 陈运泰, 祁贵仲. 地球物理学基础[M]. 北京: 科学出版社, 1985. | |
| 雷湘鄂, 许厚泽, 孙和平. 利用超导重力观测资料检测地球自由振荡[J]. 科学通报, 2002, 47(18): 1432-1436. | |
| 雷湘鄂, 许厚泽, 孙和平. 由5个国际超导重力仪台站资料检测到的秘鲁8.2级大地震所激发的球型自由振荡现象[J]. 中国科学:地球科学, 2004, 34(5): 483-491. | |
| 雷湘鄂, 孙和平, 许厚泽, 石耀霖. 苏门达腊大地震激发的地球自由振荡及其谱线分裂的检测与讨论[J]. 中国科学:地球科学, 2007, 37(4): 504-511. | |
| 栾威, 申文斌, 贾剑钢. 利用VP型垂直摆倾斜仪观测数据检测2011日本MW 9.0级地震激发的低频地球自由振荡[J]. 地球物理学报, 2015, 58(3): 844-856. | |
| 吕永清, 蔡亚先, 周云耀. 用JCZ-1超宽频带数字地震仪观测地球自由振荡[J]. 地壳形变与地震, 1997, 17(3): 103-105. | |
| 邱泽华, 马瑾, 池顺良, 等. 钻孔差应变仪观测的苏门答腊大地震激发的地球环型自由振荡[J]. 地球物理学报, 2007, 50(3): 797-805. DOI:10.3321/j.issn:0001-5733.2007.03.019 | |
| 万永革, 周公威, 郭燕平, 等. 昆仑山口西地震激发的地球环型振荡[J]. 防灾减灾工程学报, 2004, 24(1): 1-7. | |
| 万永革, 周公威, 郭燕平. 中国数字地震台网记录的昆仑山口西地震的球型自由振荡[J]. 地震, 2005, 25(1): 31-40. | |
| 万永革, 盛书中, 周公威, 等. 中国数字地震台网记录的苏门答腊-安达曼地震激发的地球球型自由振荡的检测[J]. 地震学报, 2007, 29(4): 369-381. DOI:10.3321/j.issn:0253-3782.2007.04.004 | |
| 于海英, 朱元清, 寿海涛. 印度洋9.0级大地震激发的地球球型振荡和环型振荡[J]. 地球物理学进展, 2006, 21(3): 706-716. DOI:10.3969/j.issn.1004-2903.2006.03.005 | |
| Alsop L E, Sutton G H, Ewing M. Free oscillations of the earth observed on strain and pendulum seismographs[J]. J Geophys Res, 1961, 66(2): 631-641. DOI:10.1029/JZ066i002p00631 | |
| Benioff H, Press F, Smith S. Excitation of the free oscillations of the earth by earthquakes[J]. J Geophys Res, 1961, 66(2): 605-619. DOI:10.1029/JZ066i002p00605 | |
| Dziewonski A M, Gilbert F. Observations of normal modes from 84 recordings of the Alaskan earthquake of 1964 March 28[J]. Geophys J Int, 1972, 27(4): 393-446. | |
| Lamb H. On the vibrations of an elastic sphere[J]. Lond Math Soc Proc, 1881, 13(1): 189-212. | |
| Love A E H. Some problems of geodynamics[J]. Nature, 1912, 89(2228): 471-472. DOI:10.1038/089471a0 | |
| Mitsui Y, Heki K. Observation of Earth's free oscillation by dense GPS array:After the 2011 Tohoku megathrust earthquake[J]. Scientific Reports, 2012, 2: 931 DOI:10.1038/srep00931 | |
| Ness N R, Harrison C T, Slichter L B. Observations of the free oscillations of the earth[J]. J Geophys Res, 1961, 66(2): 621-629. DOI:10.1029/JZ066i002p00621 | |
| Rosat S, Sato T, Imanishi Y, et al. High-resolution analysis of the gravest seismic normal modes after the 2004 MW=9 Sumatra earthquake using superconducting gravimeter data[J]. Geophys Res Lett, 2005, 32(13): L13304 DOI:10.1029/2005GL023128 |
 2019, Vol. 40
2019, Vol. 40
