地电场是地球表面天然存在的电场,根据场源的不同可分为大地电场和自然电场。大地电场是由固体地球外部的各种电流体系与地球介质相互作用而产生的分布于地表的感应电场,具有全球性或较大区域性特征;自然电场主要源于地壳浅层,由各种物理或化学作用产生,具有局部性特征,是重要的地球物理场之一(钱家栋等,1995;钱复业等,2005;冯红武等,2010)。地震地电场前兆观测是针对地电场地表分量随时间的变化,是地震监测预报中重要的短临前兆手段之一(王同利等,2013)。然而,随着我国城市化、工业化和现代化发展速度的加快,生活社区和大型工厂逐步向城市郊区迁移,大中城市普遍建有轨道交通系统,由此产生的工业游散电流、轨道泄露电流等对地电场观测造成严重影响,观测数据受到不同程度的干扰,表现为原始波形出现周期性高频干扰,增加了有用信息的提取难度,降低了观测数据利用率(安张辉等,2011;李伟等,2013)。目前,北京、上海和天津等大城市的地电台站多受到此类干扰,如北京通州西集台、天津静海台、上海崇明台和青浦台等,预计未来受此类干扰的地电场观测台站将逐年增多,制约了地电场观测工作的开展。
针对轨道交通对地电场观测的干扰影响,席继楼等(2002)、王同利等(2013)开展了相关研究,王兰炜等(2006)提出自适应噪声消除器,邱颖(2008)、李伟等(2013)提出小波阈值滤波,安张辉等(2011)提出EMD时空尺度滤波,等等,并取得一定成效,但存在一些问题。为此,本研究提出一种基于EMD的小波阈值滤波方法,用于剔除地电场观测数据中轨道交通造成的干扰,通过对比分析滤波前后数据,检验该方法的滤波效果,并与已有滤波方法的去噪效果进行比较。
1 去噪方法 1.1 经验模态分解(EMD)及时空尺度滤波 1.1.1 经验模态分解经验模态分解(Empirical Mode Decomposition,EMD)是希尔伯特—黄变换(Hilbert-Huang Transform,HHT)的核心(Huang et al,1998),该方法能自适应地将复杂信号分解成一系列具有不同时间尺度的固有模态函数(Intrinsic Mode Function,IMF)和一个残余分量,从高频到低频的顺序依次分解,即
| $ x\left(t \right) = \sum\limits_{i = 1}^n {} {c_i}\left(t \right) + {r_n}\left(t \right) $ | (1) |
采用EMD方法分解后,各IMF分量按频率由高到低排列,据此提出时空尺度滤波:①去掉若干高频IMF分量,与其余分量重构信号,相当于低通滤波;②去掉若干低频IMF分量,与其余分量重构信号,相当于高通滤波;③同时去掉若干高频和低频IMF分量,与其余分量重构信号,为带通滤波。对于一个分解为n个IMF分量的信号x(t),有
低通尺度滤波
| $ {x_{1k}}\left(t \right) = \sum\limits_{i = k}^n {} {c_i}\left(t \right) + {r_n}\left(t \right) $ | (2) |
高通尺度滤波
| $ {x_{{\rm{h}}k}}\left(t \right) = \sum\limits_{i = 1}^k {} {c_i}\left(t \right) $ | (3) |
带通尺度滤波
| $ {x_{{\rm{b}}k}}\left(t \right) = \sum\limits_{i = {\rm{h}}}^k {} {c_i}\left(t \right) $ | (4) |
公式(2)—(4)中,n为IMF分量个数,k为滤波时选取IMF分量阶数。
1.2 小波阈值去噪算法小波阈值去噪方法由Weaver等(1991)提出,Donoho等(1994)做了系统阐述。利用该方法处理数据,在均方误差意义下可达近似最优。一维信号的小波阈值去噪一般需以下步骤:①对含噪信号进行小波分解。选择一个小波基并确定分解的层次N,对信号进行N层小波分解;②对小波系数进行阈值处理。对分解得到的各层系数选择一个阈值,并对小波系数进行阈值处理;③信号重建。降噪处理系数经小波逆变换重建,恢复原始信号。
1.3 基于EMD的小波阈值滤波算法对于环境激励下的结构输出信号,因有用信号幅值小,用小波阈值去噪算法处理效果不理想。EMD时空尺度滤波方法是一种粗糙的去噪方法,只是简单地用原始信号减去一个或多个IMF分量以实现滤波,容易将相应分量的有用信号与干扰同时滤除,导致信号严重失真。考虑到噪声分解后分布在各IMF分量上,结合小波阈值去噪方法的特点,对所有IMF分量进行相同的小波阈值去噪处理,与小波变换相比,去噪效果可能较好(杜修力等,2007)。因此,提出基于EMD的小波阈值去噪方法。该算法具体步骤为:①对信号x(t)进行EMD分解,得到各IMF分量;②对所有IMF分量选择一种阈值确定准则,并估计各分量阈值;③选择一种阈值函数,结合各分量上的阈值估计值进行去噪计算,得到去噪后各IMF分量;④使用噪后的IMF分量重构信号,得到x(t)的去噪信号x′(t),则
| $ x'\left(t \right) = \sum\limits_{k = 1}^n {} {{c'}_k}\left(t \right) + {{r'}_n}\left(t \right) $ | (5) |
式中,x′(t)为去噪信号;
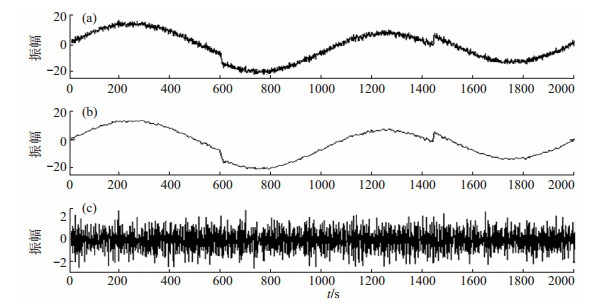
在仿真试验中,选取Heavesine信号(该信号属于含高斯白噪声的信号,数据长度为2 048个点数),验证基于EMD的小波阈值滤波方法的去噪效果。去噪效果优劣的评价标准为:①去噪后信号方差与无噪声时越接近,去噪效果越好;②去噪后信噪比越大,去噪效果越好。在对仿真信号去噪时,小波基函数选取db4函数,采用Birge-Massart策略确定阈值,对细节信号进行软阈值处理,仿真信号去噪效果见图 1和表 1。由图 1可见,基于EMD的小波阈值滤波方法可消除噪声,并保留原始信号形态。由表 1可见,原始信号经去噪处理,信噪比提高,方差减小。可见,该滤波方法去噪效果较好,可最大程度地保留原始信号中的有用信息。
|
图 1 仿真信号去噪结果 (a)原始信号;(b)滤波后的波形;(c)噪声曲线 Fig.1 The denoising results of simulation signal |
| 表 1 仿真信号去噪前后各参数对比结果 Tab.1 Comparison of parameters before and after the simulation signal denoising |
天津静海台地电场观测受城市轨道交通干扰多年,观测数据变化幅度较大,观测曲线发生畸变,不能简单判断日变形态等特征,观测资料使用价值受到较大影响。为此,使用基于EMD的小波阈值滤波方法处理该台地电场原始观测数据。
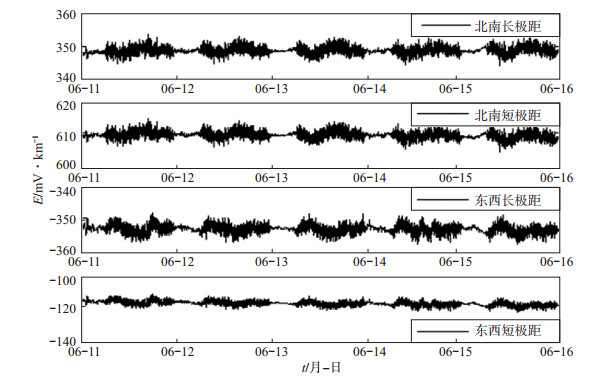
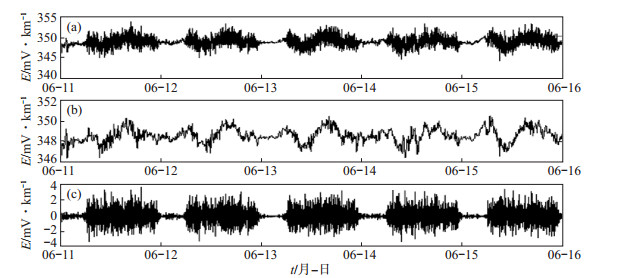
3.1 原始波形以2014年6月11日—15日天津静海台地电场原始观测数据的7 200个数据点为例,分析该处理方法的效果。5日原始数据曲线见图 2,可见:在4个测道曲线上,每日约6时—23时,均有规律的高频干扰出现,与天津地铁运行时间一致,在地铁停运的夜间时段(00时—05时),地电场观测数据变化较平稳,可见该干扰由地铁运行造成。限于篇幅,文中仅提供静海地电场台站NS向长极距数据处理结果。
|
图 2 天津静海台地电场原始波形 Fig.2 The geoelectric original waveform observed by Jinghai station, Tianjin |
采用EMD时空尺度滤波、小波阈值滤波和基于EMD的小波阈值去噪等3种方法,对天津静海台NS向长极距地电场观测数据进行处理,试图剔除地铁干扰。
3.2.1 3种方法处理结果(1)经验模态分解(EMD)及时空尺度滤波。天津静海台NS向长极距地电场观测数据经验模态分解示意见图 3,图中从上到下为第1阶—11阶固有模态函数曲线及残余分量曲线。由图 3可见,静海台记录的地铁干扰主要存在于1—3阶固有模态函数中。利用EMD时空尺度滤波方法进行低通尺度滤波,滤波效果见图 4,可见地铁干扰已基本消除。

|
图 3 NS向长极距经验模态分解示意 Fig.3 Sketch of empirical mode decomposition of North-South long pole pitch |
|
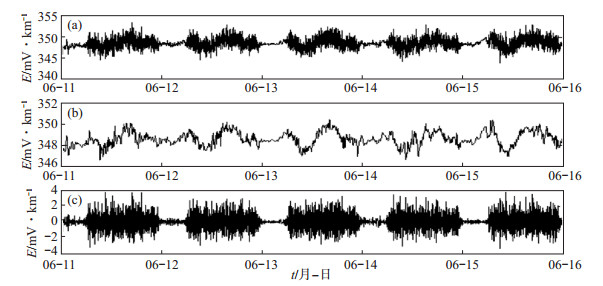
图 4 静海台地电场信号EMD滤波去噪示意 (a)原始信号曲线;(b)滤波后曲线;(c)噪声曲线 Fig.4 Sketch of EMD-based denoising of geoelectric field signal observed by Jinghai Seismic Station |
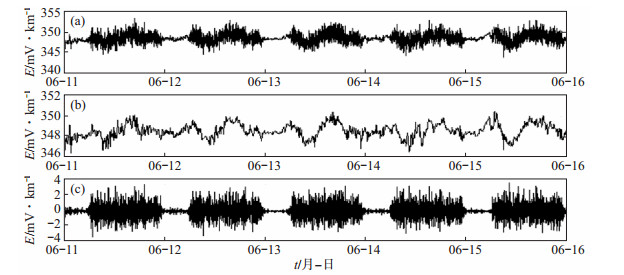
(2)小波阈值及基于EMD的小波阈值去噪。选取小波基db4函数,对地电场观测数据进行3层小波分解;应用Matlab函数库提供的wdcbm函数,采用Birge-Massart策略求取阈值;阈值函数选取软阈值,利用wdencmp函数对地电场信号进行消噪处理。去噪效果分别见图 5、图 6,可见2种方法均能基本滤除地电场信号中的地铁干扰,并同时保留原始信号中的微小突变。由噪声曲线可知,静海台NS向长极距噪声主要干扰强度在±4 mV/km。
|
图 5 静海台地电场信号小波阈值去噪示意 (a)原始信号曲线;(b)滤波后曲线;(c)噪声曲线 Fig.5 Sketch of wavelet threshold denosing of geoelectric field signal observed by Jinghai Seismic Station |
|
图 6 静海台地电场信号基于EMD小波阈值去噪示意 (a)原始信号曲线;(b)滤波后曲线;(c)噪声曲线 Fig.6 Sketch of EMD-based wavelet threshold denosing of geoelectric field signal observed by Jinghai Seismic Station |
Hilbert边际谱对每个频率提供振幅测量,可表达整个时间段内的振幅累积,由该边际谱可见所研究时间序列的优势频率。
为便于比较以上3种方法的去噪效果,对静海台地电场信号,利用希尔伯特—黄变换方法(HHT),得到去噪前后Hilbert边际谱,结果见图 7和图 8。
|
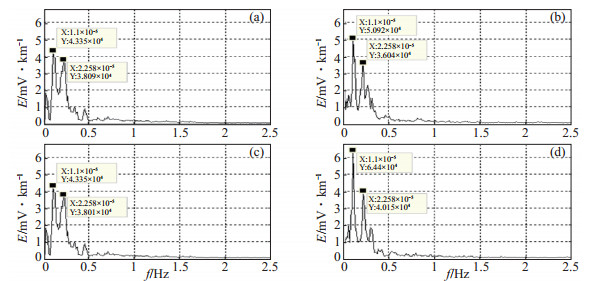
图 7 静海台地电场信号去噪前后边际谱 (a)原始信号;(b)小波去噪后;(c)EMD去噪后;(d)基于EMD的小波去噪后 Fig.7 Marginal spectrum of the geoelectric field signal before and after denosing at Jinghai Seismic Station |
|
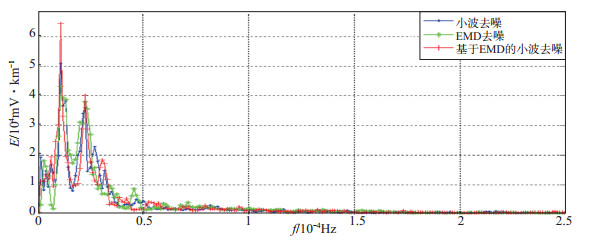
图 8 静海台地电场信号去噪后边际谱 Fig.8 Marginal spectrum map of the geoelectric field signal after denosing at Jinghai station |
由图 7可见,静海台地电场原始信号优势频率以周日波24小时(1.1×10-5 Hz)和半日波12小时(2.258×10-5 Hz)信号为主,此时信号能量最强。对原始地电场信号采用以上3种方法进行滤波,可知:①由时域曲线可见,地电场观测资料不再受地铁漏电干扰压制,地电场数据变化稳定,呈现较清晰的日变形态;②由频域角度,结合图 8进行分析,发现滤波后地电场信号优势频率未变,但其周日波和半日波分别对应的幅值有所不同,其中:基于EMD的小波阈值去噪后地电场信号边际谱幅值最大,说明该方法既能滤除地电场信号中的地铁干扰,又能突出原始信号中的有用信息;采用EMD时空尺度滤波方法,滤波前后地电场信号优势频率对应幅值基本不变,这是因为,该方法去噪过程在时域中进行,滤波时仅对经验模态分解后的前几阶固有模态函数进行减法,且模态函数幅值较小。引入均方根误差(RMSE)、信噪比(SNR)和峰值误差(PE)作为评价指标(段晨东等,2004)。
| $ {\rm{RMSE = }}\sqrt {\frac{1}{N}{{\sum\limits_{i = 1}^N {\left({{x_i} - {{\hat x}_i}} \right)} }^2}} $ | (6) |
| $ {\rm{SNR = 10log}}\frac{{\sum\limits_{i = 1}^N {x_i^2} }}{{{{\sum\limits_{i = 1}^N {\left({{x_i} - {{\hat x}_i}} \right)} }^2}}} $ | (7) |
| $ {\rm{PE = }}\mathop {\max }\limits_{i = 1}^N \left({|{x_i} - {{\hat x}_i}|} \right) $ | (8) |
式中,xi为原始信号在i时刻的采样值,
天津静海台地电场信号采用以上3种去噪方法去除地铁干扰后,利用公式(6)—(8),分别得到RMSE、SNR和PE评价指标,结果见表 2。由表 2可知,与小波阈值和EMD去噪法进行对比,采用基于EMD的小波阈值去噪法进行降噪,能够得到较高的信噪比和较低的均方根误差及峰值误差,表明利用该方法去除地电场信号中的地铁干扰是可行的,去噪效果较好。
| 表 2 地电场受地铁干扰信号去噪前后参数对比结果 Tab.2 Comparison results of parameters before and after the metro interference geoelectric field signal denoising |
利用基于EMD的小波阈值滤波方法,对天津静海台地电场观测资料中的轨道交通干扰进行处理,并将采用小波阈值去噪法和EMD去噪法的效果进行比较,得到以下结论:①3种去噪方法均可基本滤除地电场信号中的地铁干扰,并同时保留原始信号中微小的突变,使地电场观测资料不再受地铁漏电干扰的压制,观测资料数据变化恢复到应有的变化形态,使得地电场台站观测数据使用率得到提高;②基于EMD的小波阈值滤波方法既充分利用EMD时空尺度滤波和小波阈值滤波的优点,又可避免2种方法的缺点,能更加有效地消除地电场观测资料中轨道交通的干扰,且能突出原始信号中的有用信息。
总之,基于EMD的小波阈值滤波方法可作为一种滤除地电场观测资料中轨道交通干扰的新方法,也可在其他地球物理观测资料进行推广,甚至于地电场与地电阻率同场地观测中人工供电干扰信号的剔除。
| 安张辉, 杜学彬, 元丽华, 等. HHT方法在受城市轨道交通干扰地电场观测数据中的应用[J]. 地震学报, 2011, 33(2): 243-251. DOI:10.3969/j.issn.0253-3782.2011.02.011 | |
| 杜修力, 何立志, 侯伟. 基于经验模态分解(EMD)的小波阈值除噪方法[J]. 北京工业大学学报, 2007, 33(3): 265-272. DOI:10.3969/j.issn.0254-0037.2007.03.009 | |
| 段晨东, 何正嘉. 第二代小波降噪及其在故障诊断系统中的应用[J]. 小型微型计算机系统, 2004, 25(7): 1341-1343. DOI:10.3969/j.issn.1000-1220.2004.07.057 | |
| 冯红武, 朱振家, 丁宏, 等. 用FFT消除地电观测对地磁数据的干扰[J]. 地震地磁观测与研究, 2010, 31(4): 83-85. DOI:10.3969/j.issn.1003-3246.2010.04.015 | |
| 李伟, 马钦忠, 宋志平, 等. 小波变换在地电场数据分析中的应用[J]. 地震学报, 2013, 35(1): 26-35. DOI:10.3969/j.issn.0253-3782.2013.01.004 | |
| 钱复业, 赵玉林. 地电场短临预报方法研究[J]. 地震, 2005, 25(2): 33-40. | |
| 钱家栋, 林云芳. 地震电磁观测技术[M]. 北京: 地震出版社, 1995: 6-9. | |
| 邱颖.地电场观测中已知源干扰抑制研究[D].北京: 中国地震局地震预测研究所, 2008. http://cdmd.cnki.com.cn/Article/CDMD-85405-2008129230.htm | |
| 王兰炜, 赵家骝, 庞丽娜. 自适应噪声消除器在地电场观测数据处理中的应用[J]. 地震, 2006, 26(1): 87-92. | |
| 王同利, 胡乐银, 崔博闻, 等. 北京城市轨道交通对地电场观测的干扰影响[J]. 地震地质, 2013, 35(4): 887-893. DOI:10.3969/j.issn.0253-4967.2013.04.017 | |
| 席继楼, 赵家骝, 王燕琼, 等. 地电场观测技术研究[J]. 地震, 2002, 22(2): 47-53. | |
| Donoho D L, Johnstone I M. Ideal spatial adaptation by wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 | |
| Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 | |
| Weaver J B, Xu Y S, Healy D M Jr, et al. Filtering noise from images with wavelet transforms[J]. Magnetic Resonance in Medicine, 1991, 21(2): 288-295. DOI:10.1002/mrm.1910210213 |
 2019, Vol. 40
2019, Vol. 40

