2. 中国呼和浩特 010010 内蒙古自治区地震局
2. Earthquake Agency of Inner Mongolia Autonomous Region, Hohhot 010010, China
受经济发展及人类活动的影响, 乌兰浩特地震台地震观测资料中出现较多干扰信号, 如人工地震、爆破等, 此类干扰波形类似于地震波形, 会在一定程度上影响地震事件识别的有效性及准确性(包淑娴, 2011), 若不能及时准确地剔除干扰, 必将影响以后的地震研究工作(边银菊, 2002), 因此, 增强波形识别能力, 为乌兰浩特地震台爆破及地震波形记录提供有效的识别判据, 具有重要意义。
近年来, 关于天然地震与爆破的识别, 主要研究方向如下:①根据震相特征识别天然地震和爆破, 如:王婷婷等(2011)给出快速识别天然地震与人工爆破的5种震相特征判据; 王婷婷(2015)根据振幅衰减特性研究地震与爆破; 包淑娴(2011)对比研究了天然地震和人工爆破波形; 杨锐(2016)根据震相特征, 建立河北数字地震台网典型震例库; ②根据各种算法识别天然地震和爆破, 如:边银菊等(2002)使用学习向量化(learning vector quantization, 简写为LVQ)识别地震与爆破; 边银菊(2002)采用遗传BP网络识别地震与爆破, 并将Fisher方法应用于mb/MS判据, 定量得到全球普适的识别方程; 李夕海等(2009)采用最近邻支撑向量特征线融合算法、黄汉明等(2010)采用SVC算法识别天然地震与爆破。
小波分析方法是一种时间—频率分析方法, 具有多分辨率分析的特点。对于乌兰浩特地震台记录到的近震及爆破, 小波分析方法拥有多种小波函数, 根据数据特征, 可以使用最佳小波函数, 而且小波分析方法能够提取出多种有效的波形特征, 在波形特征提取时小波包变换方法能够对低频信号及高频信号逐层分解, 为爆破及地震事件的识别提供更有效的数据基础。本文在基于前人研究基础上, 对于乌兰浩特地震台记录的爆破及地震波形, 采用离散小波变换、静态小波变换及小波包变换方法, 使用db4小波基函数进行4层小波分解(边银菊, 2002), 采用第4层分解系数提取地震及爆破的3种波形特征, 即能量比特征、香浓熵特征、对数能量熵特征, 使用v—SVC支持向量分类机, 对不同小波变换提取的不同波形特征组合进行爆破与地震的识别效果检验。
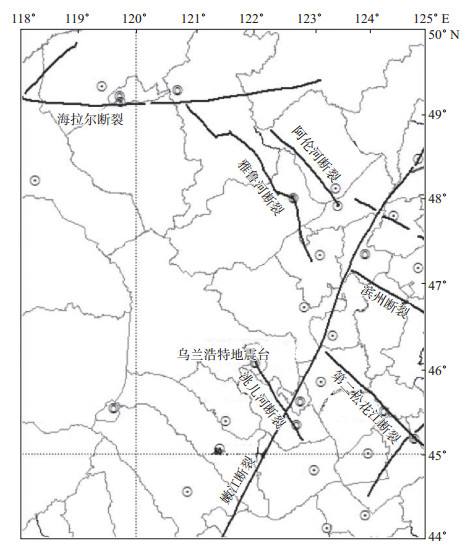
1 台站观测背景乌兰浩特地震台(下文简称乌兰浩特台)位于内蒙古自治区东北部兴安盟乌兰浩特境内, 为国家有人执守数字化测震台, 始建于1972年, 隶属内蒙古自治区地震局, 负责监测分析地震事件。乌兰浩特区域地处新华夏系大兴安岭隆起带中段, 东南与松辽坳陷相邻。该区位于蒙古弧形构造带东西翼, 为新华夏系包容、复合华夏系构造。区内主要分布洮儿河断裂、嫩江断裂、第二松花江断裂及滨州断裂, 台站及主要断裂分布见图 1。
|
图 1 台站及主要断裂分布 Fig.1 Distribution of stations and major fault zones |
随机选取2017年1月到2018年8月乌兰浩特台记录的50个地震事件及50个爆破事件, 地震事件多为发生在扎兰屯地区及松原地区的近震, 爆破事件多为乌兰浩特科右前旗及通辽霍林郭勒地区爆破事件。截取事件的垂直向(BHE)分量, 使用离散小波, 静态小波及小波包方法, 提取对数能量比特征值、香农熵特征值及对数能量熵特征值, 分别进行实验分析。
3 方法原理对地震与爆破波形记录, 使用离散小波, 静态小波及小波包方法, 提取对数能量比特征、香农熵特征及对数能量熵特征。
3.1 离散小波变换(DWT)设
| $ \int_{ - \infty }^{ + \infty } {\frac{{\left| {\psi {{\left(\omega \right)}^2}} \right|}}{\omega }{\rm{d}}\omega } < + \infty $ | (1) |
则称
| $ {\psi _{a, \tau }}\left(t \right) = {\left| a \right|^{1/2}}\psi \left({\frac{{t - \tau }}{a}} \right)\;\;\;\;\;\;\;\left({a > 0, \;\tau \in R} \right) $ | (2) |
则称
| $ {\psi _{a_0^m, k{\tau _0}}} = a_0^{ - m/2}\psi \left({a_0^{ - m}t - k{\tau _0}} \right) $ | (3) |
离散小波变换为
| $ W{T_f}\left({a_0^m, k{\tau _0}} \right) = \left\langle {f\left(t \right), {\psi _{a_0^m, k{\tau _0}}}\left(t \right)} \right\rangle = a_0^{ - m/2}\int\limits_R {f\left(t \right)\psi *\left({a_0^{ - m}t - k} \right){\rm{d}}t} $ | (4) |
离散小波变换进行分解, 只保留偶数项, 丢失奇数项信息, 推出ε—采样离散小波变换方法, 其分解过程选定ε:当ε = 0时, 表示保留偶数项; 当ε = 1时, 表示保留奇数项。整个分解过程由(0, 1)组成序列:ε = ε1, ..., εn。实现ε—采样离散小波变换的算法称为静态小波变换(时召军, 2015)。
3.3 小波包分解(WPT)若子空间Ujn为函数un(t)的闭包空间, Uj2n是函数u2n(t)的闭包空间, 令un(t)满足
| $ \left\{ \begin{array}{l} {u_{2n}}\left(t \right) = \sqrt 2 \sum\limits_{k \in Z} {h\left(k \right){u_n}\left({2t - k} \right)} \\ {u_{2n + 1}}\left(t \right) = \sqrt 2 \sum\limits_{k \in Z} {g\left(k \right){u_n}\left({2t - k} \right)} \end{array} \right. $ | (5) |
当n = 0时, 尺度函数ϕ(t)= u0(t), 小波基函数φ(t)= u1(t), 则
| $ \left\{ \begin{array}{l} {u_0}\left(t \right) = \sum\limits_{k \in Z} {h\left(k \right){u_0}\left({2t - k} \right) = \phi \left(t \right)} \\ {u_1}\left(t \right) = \sum\limits_{k \in Z} {g\left(k \right){u_0}\left({2t - k} \right)\varphi \left(t \right)} \end{array} \right. $ | (6) |
称由公式(5)构造的序列
常用小波函数有Hear小波、symN小波系列、dbN系列小波、coif系列小波、bior系列小波、rbio系列小波等(边银菊, 2002), 文中使用db4小波基函数进行实验分析。
3.4 小波系数能量比若S为原始信号, 长度为m, Sj为信号S分解后第j个小波系数, 长度为n, 则Ewt(j)称为小波系数能量比(卢世军, 2010), 有
| $ {E_{wt}}\left(j \right) = 100*\sum\limits_{k = 1}^n {S_{\left({j, k} \right)}^2} /\sum\limits_{i = 1}^m {S_i^2} $ | (7) |
若S为原始信号, Si为信号S分解后的第i个小波系数, 长度为n, 则Eshannon (i)称为小波系数的香农熵(卢世军, 2010), 有
| $ {E_{{\rm{shannon}}}}\left(i \right) = - \sum\limits_{j = 1}^n {S_{\left({i, j} \right)}^2\log S_{\left({i, j} \right)}^2} $ | (8) |
若S为原始信号, Si为信号S分解后的第i个小波系数, 长度为n, 则Elog(i)称为小波系数的对数能量熵(卢世军, 2010), 有
| $ {E_{\log }}\left(i \right) = \sum\limits_{j = 1}^n {\log S_{\left({i, j} \right)}^2} $ | (9) |
利用离散小波变换、静态小波变换及小波包变换方法, 提取所选地震及爆破的能量比特征值、香农熵特征值、对数能量熵特征值(王婷婷等, 2015), 对特征向量进行标准化, 得到测试样本及训练样本的特征向量矩阵(吴爱彧, 2012), 利用支持向量分类机对各种组合进行分类效果检验。
4.1 基于小波变换的特征提取实验采用Matlab R 2015b软件进行实验验证, 主要步骤如下:基于静态小波变换、离散小波变换及小波包变换, 使用db4小波基函数提取3种波形特征能量值(能量比特征、香农熵特征及对数能量特征), 使用v—支持向量分类机, 对乌兰浩特台地震及爆破事件进行大量递推实验, 并随机选取一次爆破事件为例, 详细说明实验结果可靠性。
由爆破和地震原始波形可知:①爆破初动方向比较清晰, 且向上。P波群较强, S波相对较弱, 且衰减速度较快; ②地震事件初动方向随机性较大, 相比于爆破事件, 发生时间和地点随机, 震源深且同一震级事件面波周期小。
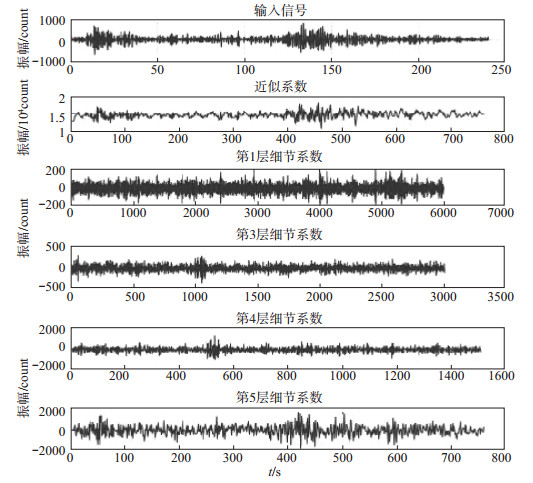
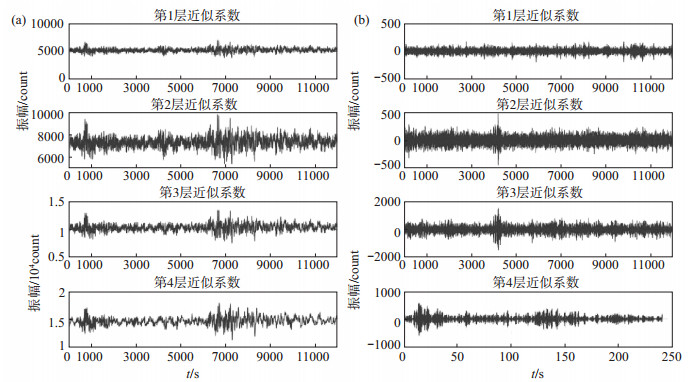
随机选取2018年8月12日11时57分扎兰屯2.6级爆破事件, 基于db4小波函数, 使用DWT、SWT、WPT等3种小波变换对爆破信号进行分解, 提取香农熵特征值, 实验结果见图 2、图 3、图 4。
|
图 2 DWT信号分解(db4) Fig.2 DWT signal decomposition(db4) |
|
图 3 SWT信号分解(db4) (a)近似系数; (b)细节系数 Fig.3 SWT signal decomposition(db4) |

|
图 4 WPT信号分解(db4) Fig.4 WPT signal decomposition (db4) |
基于db4的DWT信号分解是, 在第1层分解出信号的低频近似信号, 然后对其进行下一层分解(赵刚, 2017), 以此类推, 分解到第4层时, 得到一个5维低频近似信号及高频细节系数的特征向量(郑培玲, 2014), 见图 2。WPT不仅对信号的低频近似部分逐层分解, 同时对高频细节部分进行同样分解。因此, 基于db4的WPT信号分解, 对信号进行到第4层分解后, 分解系数有24个(庄会伟, 2017), 见图 4。对信号进行分解, 应用公式(7)—(9)计算地震及爆破波形对应的3种波形特征参数, 组成5维(DWT)、8维(SWT)、16维(WPT)的特征向量。
4.2 基于v—支持向量机的分类实验为了研究乌兰浩特台天然地震及人工爆破事件的最佳特征提取方法, 使用郭丽娟等(2008)研究的标准化的v—SVC分类器进行实验验证(v—SVC中的v取值0.5), 利用支持向量机算法, 对地震及爆破事件的样本数据训练后得到分类器, 使用测试数据进行分类结果评价。
随机选取50个地震事件及50个爆破事件, 基于db4小波基函数, 使用DWT、SWT、WPT变换方法, 提取事件的能量比特征值、香农熵特征值及对数能量熵特征值, 使用v—SVC分类器进行分类实验, 实验结果见表 1。
| 表 1 分类实验结果 Tab.1 Experiment results with different classification |
对于乌兰浩特台天然地震及人工爆破识别判据可靠性, 由表 1可知:①基于变换类型的分类实验, 使用WPT变换方法对数据进行信号分解, 分解结果最佳; ②基于波形特征的分类实验, 香农熵特征值分类效果最佳。
综合分析认为, 对于乌兰浩特台记录的天然地震及人工爆破事件, 使用WPT(db4)提取的香农熵特征进行分类, 效果最佳, 准确率达94%。
5 结论通过前期对乌兰浩特台记录的大量事件资料进行整理, 可知:①近震大多发生在扎兰屯市及松原地区; ②爆破大多发生在乌兰浩特科右前旗及霍林郭勒; ③爆破波形具有初动向上、纵波发达、面波较弱、衰减较快、震源较浅等特征。
为准确判定乌兰浩特台记录的天然地震(近震)与爆破事件, 通过大量实验, 得到以下结论:①可使用小波分析方法分析并判定近震及爆破波形特征; ②通过小波包变换提取波形特征, 对后期分类效果最佳; ③使用香农熵特征进行分类, 效果最佳; ④小波包(WPT)+香农熵特征+ v—SVC组合, 分类精度达94%, 可为乌兰浩特台自动识别地震及爆破软件提供判断依据。
| 包淑娴. 天然地震和人工爆破波形特征对比分析[J]. 华北地震科学, 2011, 29(1): 15-19. DOI:10.3969/j.issn.1003-1375.2011.01.004 | |
| 边银菊, 邹立晔. 学习向量量化(LVQ)在地震和爆破识别中的应用[J]. 地震地磁观测与研究, 2002, 23(1): 10-15. DOI:10.3969/j.issn.1003-3246.2002.01.002 | |
| 边银菊. 遗传BP网络在地震和爆破识别中的应用[J]. 地震学报, 2002, 24(5): 516-524. DOI:10.3321/j.issn:0253-3782.2002.05.009 | |
| 边银菊. Fisher方法在震级比mb/MS判据识别爆炸中的应用研究[J]. 地震学报, 2005, 27(4): 414-422. DOI:10.3321/j.issn:0253-3782.2005.04.008 | |
| 郭丽娟, 孙世宇, 段修生. 支持向量机及核函数研究[J]. 科学技术与工程, 2008, 8(2): 487-490. DOI:10.3969/j.issn.1671-1815.2008.02.041 | |
| 黄汉明, 边银菊, 卢世军, 等. 天然地震与人工爆破的波形小波特征研究[J]. 地震学报, 2010, 32(3): 270-276. DOI:10.3969/j.issn.0253-3782.2010.03.002 | |
| 李夕海, 刘刚, 刘代志, 等. 基于最近邻支撑向量特征线融合算法的核爆地震识别[J]. 地球物理学报, 2009, 52(7): 1816-1824. DOI:10.3969/j.issn.0001-5733.2009.07.016 | |
| 卢世军, 黄汉明. 震源识别中小波变换类型的选择研究[J]. 信息技术, 2010, 11061106(7): 13-16. DOI:10.3969/j.issn.1009-2552.2010.07.004 | |
| 时召军, 朱梅, 周迪, 等. 不同小波函数对灰色模型精度影响分析[J]. 水文, 2015, 35(3): 49-52. DOI:10.3969/j.issn.1000-0852.2015.03.009 | |
| 王婷婷, 边银菊. 识别天然地震和人工爆破的判据选择[J]. 地震地磁观测与研究, 2011, 32(6): 62-67. DOI:10.3969/j.issn.1003-3246.2011.06.012 | |
| 王婷婷, 边银菊. 振幅衰减特性在地震与爆破识别中的应用[J]. 地震学报, 2015, 37(1): 169-179. | |
| 吴爱彧. 小波分析在经济问题中的应用[J]. 经济研究导刊, 2012, 11061106(21): 1-3. DOI:10.3969/j.issn.1673-291X.2012.21.001 | |
| 杨锐, 魏艳旭, 刘丽, 等. 河北数字地震台网近震震相特征与典型震例库的建立[J]. 高原地震, 2016, 28(1): 4-13. DOI:10.3969/j.issn.1005-586X.2016.01.002 | |
| 赵刚.地震信号自动截取算法与震源类型识别研究[D].桂林: 广西师范大学, 2017. | |
| 郑培玲. 平顶山地区爆破识别判据分析[J]. 地震地磁观测与研究, 2014, 35(5): 84-87. | |
| 庄会伟.基于视觉的静态手势识别中关键技术的研究[D].济南: 山东大学, 2017. |
 2019, Vol. 40
2019, Vol. 40


