2. 中国河北 050021 河北省地震局
2. Hebei Earthquake Agency, Shijiazhuang 050021, China
地震由地球内部的急剧变动引起, 地壳在能量快速释放的过程中造成振动, 产生地震波(宇津德治, 1990)。地震发生时断层的力学机制和错动断层的运动类型可由震源机制解给出。震源机制解含有大量震源应力场和震源破裂错动信息, 可用于探讨震源类型、力学成因以及破裂过程, 对于地震研究、孕震机理解释以及震后应力分布状态分析具有重要意义。随着我国数字地震台网的发展, 积累了大量数字地震资料, 确定中小地震震源机制解已成为区域数字地震台网的紧迫任务。不断积累的中小地震震源机制解, 将为研究区域的构造应力场变化及地震活动性等提供重要的数据参考。
Dreger等(1993)提出一种区域广义体波反演方法(即P波之后面波之前的波列称为Pnl波, 反演方法简称Pnl波方法), 用于稀疏台网和单台反演震源机制; Zhao等(1994)提出CAP方法, 经Zhu等(1996)改进, 通常用于确定区域和地方范围内3—5级地震的震源机制。上述方法均不适用于小震和微小震的震源机制求解。对于小震, 可以采用以下方法求解震源机制:①P波初动方法, 对台站布局和台站数量依赖性相对较强, 受到较大限制(许忠淮等, 1983; Hardebeck et al, 2002; 俞春泉等, 2009); ②初动与振幅相结合的方法, 如:梁尚鸿等(1984)利用初动符号与垂直向SV/P振幅比结合方法, 测定海城地震前震序列震源参数; 吴大铭等(1989)利用初动符号与水平向SH/P振幅比结合方法, 求得震源参数最小二乘解, 并确定河北滦县震群震源机制等; Snoke(1989)利用P、SV、SH的极性和振幅SV/P、SH/P、SV/SH等信息的任意组合, 编写程序并不断改进, 是对初动—振幅法的全面总结; 严川等(2014)提出广义极性振幅技术(Generalized Polarity and Amplitude Technique, 简称GPAT), 通过实验数据和具体实例验证, 得到利用P波初动和与振幅相结合研究小震及微震的广义极性振幅技术法(GPAT)。
GPAT把观测场与合成场的相似性作为求解目标, 充分利用最大振幅的极性做为求解目标, 不仅适用于小震和微震的震源机制求解, 且允许反演中强地震的震源机制, 除了考虑P波初动的极性, 无论P波、S波或面波, 只要波形记录上表现出明显的震相特征, 最大振幅即可被采用。一系列数值试验及检验, 证明了GPAT的可行性, 其抗干扰能力较强, 更适用于震相复杂区域的震源机制解反演。
鉴于GPAT方法对求解小震及微震震源机制的优势, 利用广义极性振幅技术方法(严川等, 2014, 2015), 计算河北南部及邻近地区中小地震震源机制, 为研究该区构造应力场变化及地震活动性提供重要参考数据, 更好地服务于区域地震监测工作。
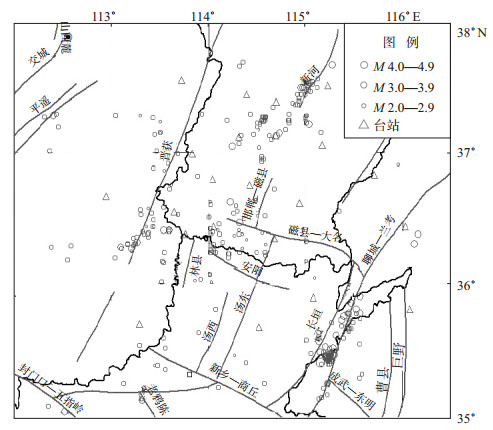
1 研究区及资料选取河北南部及邻近地区(35.00°—38.00°N, 112.00°—116.50°)位于太行山隆起区和华北平原沉降带交界处南部, 东部与鲁西隆起区(华北地块一级构造单元)为邻。河北南部及邻区为华北地块一级构造单元, 包括鲁西隆起、华北坳陷和太行山隆起3个不同性质的构造单元, 各级断块均以规模较大、切割较深、活动性相对较强的断裂为界。该区主要断裂带有太行山断裂、邯郸断裂、邢台东断裂、聊城—兰考断裂、晋获断裂、磁县—大名断裂、林县断裂、菏泽断裂、临漳—大名断裂、安阳断裂、新乡—商丘断裂、涉县断裂、井陉—左权断裂等(图 1)。
|
图 1 河北南部及其邻近地区台站、震中及断裂带分布 Fig.1 Distribution of stations, epicenters and fault zones in southern Hebei and its adjacent areas |
河北南部及邻区历史地震活动频繁, 典型中强地震有1830年磁县7.5级地震、1889年大名5级地震、1937年菏泽7.0级地震、1966年邢台7.2级地震。近年来, 河北、山西交界地区和河南范县及附近地区中小地震相对较多, 河北的邢台、磁县和山东的菏泽等老震区小震活动不断(张丽晓等, 2016)。
作为河北省第一个遥测台网, 邯郸地震台网始建于1981年, 位于晋、冀、鲁、豫交界地区, 囊括23个地震台站, 至今已积累大量地震波形数据。收集整理邯郸地震台网2007—2016年记录的河北南部及邻区中小地震(图 1), 按以下原则进行筛选:至少被6个以上台站记录, 且至少一个台站Pg波初动记录清晰, 共得到震中距15—200 km的368次地震参与震源机制解反演, 以便为后续研究提供数据资料。
2 方法原理地震产生的地表位移(严川等, 2014, 2015)一般可以表示为
| $ \mu \left({x, t} \right) = {u_j}{e_j} $ | (1) |
式中, j = 1, 2, 3, 分别代表东西、北南和垂直(上下)3个方向; uj代表P波、S波、面波或其他震相位移分量。uj可以表示为
| $ {\mu _j} = u_j^{\rm{P}} + u_j^{\rm{S}} + u_j^{\rm{F}} + u_j^{\rm{O}} $ | (2) |
式中, P、S、F和O分别表示P波、S波、面波和其他震相, 为便于讨论问题, 只考虑P波、S波和面波的情形。
地震波场在时间和空间上是连续的, GPAT只需要有限观测点记录的P波、S波和面波带有极性的最大振幅以及P波初动极性, 由此分别建立2个行矢量
| $ {v_1} = \left[ {{a_{ijk}}} \right] $ | (3) |
| $ {v_2} = \left[ {{b_{ijk}}} \right] $ | (4) |
式中, i = 1, 2, ..., N, 表示不同观测点; j = 1, 2, 3, 分别代表东西、北南和垂直(上下)3个方向; k = 1, 2, 3, 分别表示直达P波、S波和面波; a为矢量v1的元素, 表示带有极性且绝对值最大振幅; b为矢量v2的元素, 代表P波初动极性(b = +1代表初动向东、北和上, b = -1代表初动向西、南和下, b = 0代表初动方向不明确)。
对于给定震源产生的波场, 可以写出类似矢量
| $ {v'_1} = \left[ {{{a'}_{ijk}}} \right] $ | (5) |
| $ {v'_2} = \left[ {{{b'}_{ijk}}} \right] $ | (6) |
为便于建立目标函数, 令
| $ \eta = \left[ {{v_1}\omega {v_2}} \right] = {\left[ {{a_{ijk}}\omega {b_{ijk}}} \right]^{\rm{T}}} = \left[ {{\alpha _m}} \right] $ | (7) |
| $ \eta ' = \left[ {{{v'}_1}\omega {{v'}_2}} \right] = {\left[ {{{a'}_{ijk}}\omega {{b'}_{ijk}}} \right]^{\rm{T}}} = \left[ {{\beta _m}} \right] $ | (8) |
式中, ω为振幅信息与P波信息的相对权重, αm为观测矢量元素, βm为合成矢量元素, T表示行矢量向列矢量的转置。
若给定震源的标量地震矩、震源位置和震源机制与实际震源相同, 则
| $ \eta ' = \eta $ | (9) |
若仅标量地震矩不同而其他参数相同, 则二者相似, 那么η′和η线性相关。令ρ为二者的相关系数, 则
| $ \rho = \frac{{\sum\limits_m^M {\left({{\alpha _m} - \bar \alpha } \right)\left({{\beta _m} - \bar \beta } \right)} }}{{\sqrt {\sum\limits_m^M {{{\left({{\alpha _m} - \bar \alpha } \right)}^2}} } \sqrt {\sum\limits_m^M {{{\left({{\beta _m} - \bar \beta } \right)}^2}} } }} $ | (10) |
式中,
相对权重ω依赖于aijk和bijk, 为了阐述ω的取值问题, 定义2个向量X和Y, 并讨论其相关系数k, 则
| $ X = {\left[ {{a_{ijk}}\omega {b_{ijk}}} \right]^{\rm{T}}} = \left[ {{x_m}} \right] $ | (11) |
| $ Y = {\left[ {{a_{ijk}} - \omega {b_{ijk}}} \right]^{\rm{T}}} = \left[ {{y_m}} \right] $ | (12) |
| $ k = \frac{{\sum\limits_m^M {\left({{x_m} - \bar x} \right)\left({{y_m} - \bar y} \right)} }}{{\sqrt {\sum\limits_m^M {{{\left({{x_m} - \bar x} \right)}^2}} } \sqrt {\sum\limits_m^M {{{\left({{y_m} - \bar y} \right)}^2}} } }} $ | (13) |
不难看出, k值依赖于ω, 若ω = 0, 则k = 1, 表示仅振幅发挥作用; 若ω→+∞, 则k→-1, 表面振幅几乎不发挥作用; 当k = 0时, 振幅和极性发挥相同作用, 用ω0 = ω(k = 0)表示, ω0的大小取决于具体数据矢量X和Y。
| $ \rho = \rho \left({\varphi, \theta, \lambda, d} \right) $ | (14) |
式中, φ、θ、λ、d分别表示断层走向、倾角、滑动角和震源深度。广义极性振幅技术对不同深度通过网格搜索法, 反演ρ→1或者Δρ=1-ρ→0时的非线性求解问题, 从而得到震源机制解。
3 数据处理地震波形记录的频率相对较高, 为了消除背景噪声, 保证波形主频质量, 对所选368次地震波形数据进行滤波处理。设置滤波范围为1—4 Hz, 采样率设置为滤波上限的5倍。使用表 1所示地壳速度结构模型, 参考莘海亮等(2011)结合山西、河南、山东、河北交界地区得到的结果。利用该速度模型, 采用反射—折射率方法计算格林函数(Wang, 1999), 设置地壳深度范围为0—32 km, 间隔1 km。利用P波初动和与振幅相结合的广义极性振幅技术法(GPAT)计算得到368个中小地震的震源机制解。
| 表 1 地壳速度模型 Tab.1 Crustal velocity mode |
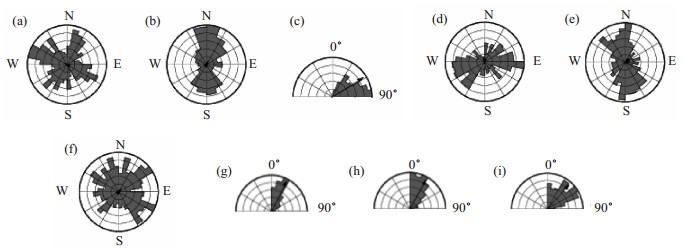
利用得到的368个中小地震的震源机制解, 通过统计分析方法, 以10°为间隔进行归一频数计算, 按照节面走向、滑动角和倾角以及P、T、B轴的方位角和倾角, 绘制对应玫瑰图, 见图 2。
|
图 2 研究区震源机制解节面参数玫瑰图 (a)走向; (b)滑动角; (c)倾角; (d)P轴方位角; (e)T轴方位角; (f)B轴方位角; (g)P轴倾角; (h)T轴倾角; (i)B轴倾角 Fig.2 Rose diagram of nodal plane and P、T axis parameters of the focal mechanism solutions in the study area |
整体而言, 研究区震源断层面节面走向主要呈NNE向和NWW向, 其中NNE向节面走向N10°—40°; NWW向节面走向N280°—310°; 滑动角以0°和180°居多, 表明发震断层以走滑运动为主, 表现为左旋走滑和右旋走滑; 断层面以倾斜或直立为主, 倾角主要在60°—90°范围内; 主压应力P轴倾角范围为10°—30°, 优势方向为NEE; 主张应力T轴倾角范围0°—50°偏多, 优势方向为NNW; 中等应力B轴(一般勾画破裂方位)分布相对凌乱, 可能与是否受区域断裂控制有关。
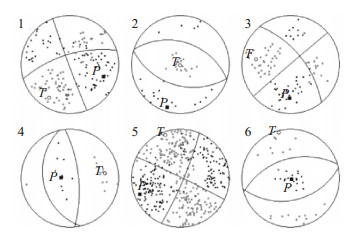
4.2 系统聚类分析采用系统聚类方法(刁桂苓等, 1992, 1995), 对计算得到的368次地震震源机制进行聚类分析。中小地震受局部影响程度和随机发生的可能性较大, 无法一一比较, 为了清晰呈现震源机制的异同, 使用最大距离法, 对368次ML ≥ 2.0地震的震源机制参数进行聚类分析, 结果显示, 所选地震震源机制解分6类, 见图 3和表 2。其中第1、3、5类平均解为走滑型, 占总数的86.3%, 其中P轴走向为NEE的占比较大, 约占总数的53.7%, P轴走向为SEE的占总数的20%;第2类平均解为逆断层, 占总数的5.4%;第4、6类平均解为正断层, 占总数的8.3%。为验证结果可靠性, 利用聚类方法分析ML ≥ 3.0地震, 同样得到P轴走向为NEE的占比重较大的结论。据李祖钦(1980)的研究, 华北地区应力场最大压应力轴呈NEE向, 最小压应力轴呈NNW向。本研究中第3类和第5类震源机制解约占总数的66.3%, 与华北构造背景应力场作用方式相似。总体来说, 河北南部及邻区断层以走滑运动为主, 应力作用方式为水平和近水平的推扭。
|
图 3 研究区各种类型解的P、T轴和平均解投影 Fig.3 P and T axis of each kind of solution and their projections of average solution |
| 表 2 研究区不同震源机制类型各平均轴参数 Tab.2 Average parameters of stress axis of each kind of solution in the study area |
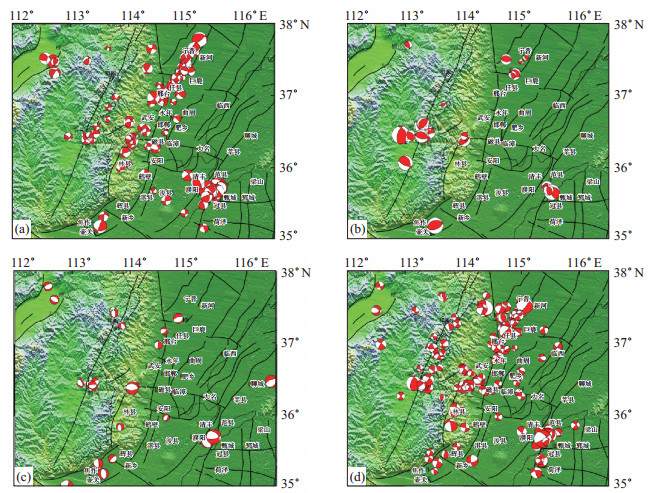
将所选地震震源机制系统聚类分析结果投影到断裂带上, 得到研究区不同类型地震震源机制解分布, 见图 4。
|
图 4 研究区不同类型地震震源机制解分布 (a)第1、3类走滑型地震; (b)第2类逆断层地震; (c)第4、6类正断层型地震; (d)第5类走滑型地震 Fig.4 Distribution of different types of focal mechanisms in the study area |
刁桂苓等(2011)指出, 不同震源机制类型对应不同应力作用模式, 正断层对应拉张应力, 逆断层对应挤压应力, 走滑断层对应水平剪切应力。由图 4可知:①走滑型地震(第1类、第3和第5类地震)主要分布于邯郸断裂、邢台东断裂、聊城—兰考断裂、晋获断裂、磁县—大名断裂、林县断裂、菏泽断裂等及附近地区; ②正断层型地震(第4类、第6类地震)主要分布于晋获断裂、邯郸断裂、邢台东断裂、聊城—兰考断裂、磁县—大名断裂、林县断裂等断裂带及附近地区; ③逆断层型地震(第2类地震)主要分布于新河断裂、聊城—兰考断裂、晋获断裂、磁县—大名断裂、林县断裂等及附近地区。
总之, 河北南部及邻近地区地震具有左旋、右旋走滑为主的断层机制特征, 表明研究区主要受水平剪切应力作用; 正断层型地震较多, 说明研究区拉张作用比挤压作用强烈。
5 结论与讨论利用P波初动和振幅相结合研究的广义极性振幅技术法(GPAT), 反演2007—2016年河北南部及邻近地区发生的368个ML ≥ 2.0中小地震震源机制解, 并利用统计分析方法进行归一频数分析, 认为:震源断层面主要呈NNE向、NWW向2组节面走向; 断层机制以左旋、右旋走滑为主; 断层面多直立或倾斜; P、T轴优势方向相对集中, B轴优势方向相对混乱, 可能受到该区断裂带控制, 需进一步研究。
利用聚类方法对该区震源机制解进行分类统计, 发现该区地震以走滑型为主, 其中:第1、3、5类平均解为走滑型机制, 占总数的85.7%;第2类平均解为逆断层型机制(占总数的6%); 第4、6类平均解为正断层型机制(占总数的8%)。第3类和第5类震源机制解约占总数的66.3%, 与华北构造构造背景应力场作用方式相似。分析认为, 中国地处欧亚板块东南角, 青藏高原在欧亚板块与印度洋板块共同作用下形成一系列巨大的弧形构造, 在与中国东部接界处产生NEE向侧向压力。由日本海沟起, 太平洋板块向西俯冲, 插入欧亚板块之下(李祖钦, 1980), 到达朝鲜半岛和中国东北, 插入深度在500 km以上, 在近EW向上造成强大的挤压力(宇津德治, 1981), 是造成华北地区地壳应力场压应力主轴为NEE—SWW向、张应力主轴为NNW—SSE向的主要原因。总体来说, 河北南部及邻区以走滑运动特征为主, 应力作用以水平和近水平推扭方式为主。
震源机制解与断裂带对应结果显示, 河北南部及邻区以走滑地震为主, 主要受水平剪切应力的作用, 且正断层型地震较多, 说明研究区拉张作用较强烈。走滑地震主要分布于邢台—邯郸断裂带、聊城—兰考断裂、晋获断裂、磁县—大名断裂、林县断裂、菏泽断裂等及附近地区, 应密切关注断裂活动状态。
严川博士、付真博士提供GPAT计算软件, 并给予相关帮助, 在此表示感谢。| 刁桂苓, 于利民, 李钦祖. 震源机制解的系统聚类分析——以海城地震序列为例[J]. 中国地震, 1992, 8(3): 86-92. | |
| 刁桂苓, 于利民, 李钦祖. 大同两次MS 5.8地震序列的震源区应力场对比分析[J]. 地震, 1995(4): 345-352. | |
| 刁桂苓, 徐锡伟, 陈于高, 黄柏寿, 王晓山, 冯向东, 杨雅琼. 汶川MW 7.9和集集MW 7.6地震前应力场转换现象及其可能的前兆意义[J]. 地球物理学报, 2011, 54(1): 128-136. DOI:10.3969/j.issn.0001-5733.2011.01.014 | |
| 李钦祖. 华北地壳应力场的基本特征[J]. 地球物理学报, 1980, 23(4): 376-388. DOI:10.3321/j.issn:0001-5733.1980.04.004 | |
| 梁尚鸿, 李幼铭, 束沛镒, 朱碚定. 利用区域地震台网P、S振幅比资料测定小震震源参数[J]. 地球物理学报, 1984, 27(3): 249-257. DOI:10.3321/j.issn:0001-5733.1984.03.005 | |
| 莘海亮, 方盛明, 李稳. 豫北及邻区地震双差法重新定位研究[J]. 大地测量与地球动力学, 2011, 31(6): 63-68. | |
| 吴大铭, 王培德, 陈运泰. 用SH波和P波振幅比确定震源机制解[J]. 地震学报, 1989, 11(3): 275-281. | |
| 许忠淮, 阎明, 赵仲和. 由多个小地震推断的华北地区构造应力场的方向[J]. 地震学报, 1983, 5(3): 268-279. | |
| 严川, 许力生. 一种地方与区域地震震源机制反演技术:广义极性振幅技术(一)——原理与数值实验[J]. 地球物理学报, 2014, 57(8): 2555-2572. | |
| 严川, 许力生, 张旭, 李春来, 许康生. 一种地方与区域地震震源机制反演技术:广义极性振幅技术(二)——对实际震例的应用[J]. 地球物理学报, 2015, 58(10): 3601-3614. DOI:10.6038/cjg20151014 | |
| 俞春泉, 陶开, 崔效锋, 胡幸平, 宁杰远. 用格点尝试法求解P波初动震源机制解及解的质量评价[J]. 地球物理学报, 2009, 52(5): 1402-1411. DOI:10.3969/j.issn.0001-5733.2009.05.030 | |
| 张丽晓, 闫俊岗, 宫猛. 利用接收函数研究邯郸及周边地区地壳结构[J]. 地震地磁观测与研究, 2016, 37(6): 21-26. DOI:10.3969/j.issn.1003-3246.2016.06.004 | |
| [日]宇津德治.地震事典[M].李欲彻, 译.北京: 地震出版社, 1990. | |
| [日]宇津德治.地震学[M].陈铁成, 全莹道, 译.北京: 地震出版社, 1981. | |
| Dreger D S, Helmberger D V. Determination of source parameters at regional distances with three-component sparse network data[J]. Journal of Geophysical Research:Solid Earth, 1993, 98(B5): 8107-8125. DOI:10.1029/93JB00023 | |
| Hardebeck J L, Shearer P M. A new method for determining first-motion focal mechanisms[J]. Bull Seismol Soc Am, 2002, 92(6): 2264-2276. DOI:10.1785/0120010200 | |
| Snoke J A. Earthquake mechanisms[M]//James D E. Encyclopedia of Geophysics. New York: Van Nostrand Reinhold Company, 1989: 239-245. | |
| Wang R J. A simple orthonormalization method for stable and efficient computation of Green's functions[J]. Bull Seismol Soc Am, 1999, 89(3): 733-741. | |
| Zhao L S, Helmberger D V. Source estimation from broadband regional seismograms[J]. Bull Seismol Soc Am, 1994, 84(1): 91-104. | |
| Zhu L P, Helmberger D V. Advancement in source estimation techniques using broadband regional seismograms[J]. Bull Seismol Soc Am, 1996, 86(5): 1634-1641. |
 2019, Vol. 40
2019, Vol. 40


