当远震震级相对较小或震源深度较深时,地震的面波不发育,无法测定远震面波震级,而地震仪器能够记录到清晰的P波和PP波,所以古登堡和里克特采用体波(P,PP,S),通常是P波来确定震级,称作体波震级。后来,体波震级被世界各国广泛应用,由于所用地震仪器和测量方法不尽相同,造成同一地震所得震级大小不一致。
我国采用短周期地震仪测定体波震级mb,中长周期地震仪测定体波震级mB。mb和mB是不同震级标度震级,针对不同频段的地震波位移,均采用古登堡提出的体波震级计算公式得到(中国地震局,2001)。其中:mb震级采用周期为0.5—2.5 s的地震体波振幅来计算;mB震级采用周期为3.5—12.0 s的地震体波振幅来计算。
本文利用库尔勒地震台(下文简称库尔勒台)2008年6月至2015年12月记录的全球数字地震观测资料,就震级大小、震中距、震源深度以及震中方位,与中国地震台网中心测定的体波震级进行对比,得到该台新的量规函数和台站校正值。
1 体波震级测定我国采用P或PP波垂直向质点运动最大速度来测定mb和mB。利用仿真DD-1短周期地震仪垂直(UD)向最大振幅和周期值计算mb,周期为0.5 s ≤ T ≤ 2.5 s;利用仿真DK-1中长周期地震仪或763长周期地震仪垂直(UD)向最大振幅和周期值计算mB,周期为3.5 s ≤ T ≤12.0 s。计算公式为
| $ m_{\mathrm{b}}或m_{\mathrm{B}}=\lg \left(\frac{A}{T}\right)_{\max }+Q({\mathit{Δ}}, h)+C $ | (1) |
式中,A为体波质点运动最大速度对应的地动位移振幅值,单位μm;T为相应周期,单位s;Q(Δ,h)是量规函数(有关震中距和震源深度的函数);C为台站校正值(中国地震局监测预报司,2003)。
2 体波震级偏差计算获得若干组震中距、震级偏差数据,其中:Mi为台站测定的第i个地震震级,M0i为中国地震台网测定的震级,Ei为震级偏差,即
| $ E_{i}=M_{i}-M_{0 i} $ | (2) |
则平均震级偏差为
| $ \Delta E_{i}=\frac{1}{N} \sum_{i=1}^{N}\left(M_{i}-M_{0 i}\right) $ | (3) |
标准偏差为
| $ \delta_{i}=\left[\frac{\sum_{i=1}^{N}\left(M_{i}-M_{0 i}\right)^{2}}{N-1}\right]^{\frac{1}{2}} $ | (4) |
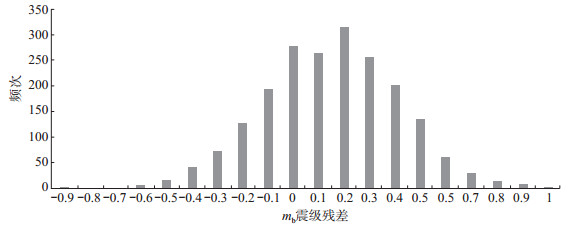
选取库尔勒台记录的2 012个mb ≥4.5地震,与中国地震台网震级进行偏差计算,得到平均偏差为0.145 5,与实际震级偏差基本吻合;标准偏差δi =±0.265 9,说明震级偏差离散程度偏大。表 1给出库尔勒台mb震级偏差与频次统计结果,可见,震级偏差在±0.2之间的地震所占比例为58.35%(刘瑞丰等,2005);震级偏差ΔMi ≥0的地震所占比例为77.29%(殷翔等,2012),而ΔMi ≥0.3的地震所占比例为34.89%,说明台站计算震级偏大。库尔勒台mb震级偏差频度分布见图 1,可见震级偏差与地震频度属正态分布,但分布曲线形态不以ΔM = 0为对称轴,其优势分布在ΔM = 0.2位置上。通过线性回归分析,得到库尔勒台与中国地震台网中心mb震级的关系,为
| $ {m_{{\rm{b台网}}}} = 0.7249{m_{{\rm{b台}}}} + 1.3530 $ |
|
图 1 库尔勒台记录mb震级偏差频次分布 Fig.1 Frequency distribution of mb magnitude deviation recorded by Korla Seismic Station |
| 表 1 mb台与mb台网体波震级偏差统计 Tab.1 Statistical of magnitude deviation of body wave in mb台 and mb台网 |
式中,mb台为库尔勒台mb震级,mb台网为中国地震台网mb震级。
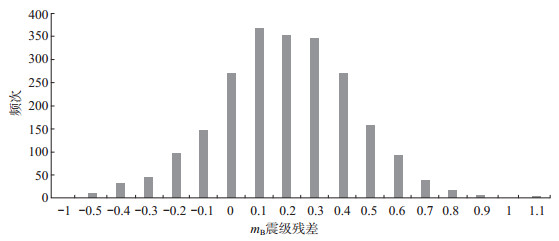
2.2 mB震级偏差选取库尔勒台记录的2 252个mB ≥4.5地震进行偏差计算,得到平均偏差为0.194 1,与震级实际计算结果基本吻合;标准偏差δi = ±0.246 9,说明震级偏差离散程度偏大。表 2为库尔勒台mB震级偏差与频次统计结果,可见震级偏差ΔMi在±0.2之间的地震所占比例为54.84%,符合观测规范标准所占比例较低;震级偏差ΔMi ≥0的地震所占比例为85.26%,而ΔMi ≥0.3的地震所占比例为41.30%,可见台站计算震级对中国地震台网编目有一定影响。库尔勒台与中国地震台网mB震级偏差频度分布见图 2,可见震级偏差频度属正态分布,曲线形态不以ΔM = 0为对称轴,其中震级偏差为0—0.4的地震频次较高,ΔM = 0.1对应优势分布。通过线性回归分析,得到库尔勒台与中国地震台网中心mB震级的关系,为
| $ {m_{{\rm{B台网}}}} = 1.0025{m_{{\rm{B台}}}} + 0.1802 $ |
|
图 2 库尔勒台记录mB震级偏差频次分布 Fig.2 Frequency distribution of mB magnitude deviation recorded by Korla Seismic Station |
| 表 2 mB台与mB台网体波震级偏差统计 Tab.2 Statistical of magnitude deviation of body wave in mB台 and mB网台 |
式中,mB台为库尔勒台mB震级,mB台网为中国地震台网mB震级。
3 震级偏差分析 3.1 震级大小与震级偏差之间的关系根据震级大小,把体波震级mb、mB各分为4档进行统计,统计结果见表 3。由表 3可见,当mb为4.5—6.9时,库尔勒台与中国地震台网震级偏差无明显区别;当mb ≥ 7.0时,因地震样本较少,震级偏差为-0.30(任克新等,2009),可能与实际结果不一致;库尔勒台与中国地震台网mB震级偏差与震级大小关系不明显。
| 表 3 震级偏差值与震级大小关系 Tab.3 Relationship between magnitude and magnitude size deviation values |
将库尔勒台记录的mb≥4.5、mB≥4.5地震,按震中距大小,分别统计不同区间地震的平均震级偏差,见表 4。由表 4可见:对于mb≥4.5地震,不同震中距区间,震级偏差相差不大,与震中距关系不明显;对于mB≥4.5地震,当震中距逐渐增大时,震级偏差随之增大,但极远震震级偏差较小,为0.08。
| 表 4 震级偏差与震中距的关系 Tab.4 The relationship between magnitude and epicentral distance |
将库尔勒台记录的mb≥4.5、mB≥4.5地震,按震源深度大小,分别统计不同震源深度范围的震级偏差,结果见表 5。由表 5可见:①对于mb≥4.5地震:震源深度在0 ≤ h ≤ 96 km,震级偏差相对较大;震源深度h>96 km,库尔勒台与中国地震台网mb震级基本一致,震级偏差不大;②对于mB≥4.5地震:当震源深度在0≤h≤96 km,震级偏差大于0.20;震源深度h>96 km,震级偏差较小。
| 表 5 震源深度与震级偏差的关系 Tab.5 The relationship between focal depth and the magnitude deviation |
将库尔勒台记录的mb≥4.5、mB≥4.5地震,按照台站方位,分别统计不同象限的震级偏差,结果见表 6。由表 6可见:①对于mb≥4.5地震:地震位于第三象限,震级偏差较小,为0.09;地震位于其他象限,震级偏差在0.2以内,接近平均偏差0.15;②对于mB≥4.5地震:地震位于第三象限,震级偏差为0.11;地震位于其他象限,震级偏差在0.2左右,接近平均震级偏差0.19。
| 表 6 震级偏差与方位角的关系 Tab.6 The relationship between magnitude deviation and azimuth |
据刘红桂(2012)的分析,介质路径不同,对地震波的固有吸收衰减和散射衰减不同,因此,震级偏差存在方位差异,应与区域地质构造及深部介质结构特征有关。
4 结论通过对库尔勒台2008—2015年以来记录的数字地震观测资料,进行体波震级对比,得到以下结论:①由统计结果可知,库尔勒台mb和mB平均偏差值分别为0.145 5、0.194 1,台站实测震级大于中国地震台网中心测定震级;②在震中距与震级偏差关系中,体波震级mb与震中距大小无直接关系,震级偏差接近平均震级;当震中距逐渐增大时,体波震级mB偏差随之增大,当震中距大于105°时,mB震级偏差较小,与中国地震台网中心测定结果基本一致;③当震源深度在0≤h≤96 km时,mb和mB震级偏差相对较大,接近台站实测平均震级;而震源深度h>96 km时,台站所计算mb和mB震级与中国地震台网震级基本一致;④根据台站方位,在第三象限,mb和mB震级偏差较小,在第一、二、四象限,mb和mB震级偏差与平均震级偏差基本一致。
| 刘红桂. 不同构造区固有吸收衰减和散射衰减相对强弱的对比研究[J]. 国际地震动态, 2012(1): 31-32. | |
| 刘瑞丰, 陈运泰, BormannP, 等. 中国地震台网与美国地震台网测定震级的对比(Ⅰ)——体波震级[J]. 地震学报, 2005, 27(6): 583-587. DOI:10.3321/j.issn:0253-3782.2005.06.001 | |
| 任克新, 徐志国, 刘瑞丰, 等. IASPEI新标准体波震级分析研究[J]. 中国地震, 2009, 25(4): 377-385. DOI:10.3969/j.issn.1001-4683.2009.04.004 | |
| 殷翔, 徐志国, 任枭, 等. 南京基准地震台与中国地震台网测定体波震级对比分析[J]. 地震地磁观测与研究, 2012, 33(2): 21-26. DOI:10.3969/j.issn.1003-3246.2012.02.004 | |
| 中国地震局. 地震及前兆数字观测技术规范.地震观测(试行)[M]. 北京: 地震出版社, 2001: 12-13. | |
| 中国地震局监测预报司. 地震参数——数字地震学在地震预测中的应用[M]. 北京: 地震出版社, 2003: 10-11. |
 2019, Vol. 40
2019, Vol. 40

