0 引言

准确确定地震震源深度对于准确评估地震灾害，确定地震成因和动力学环境，判断余震发展趋势和危险性以及监测核爆等具有重要意义。目前，在地震深度定位方法可分为走时定位法和波形反演法2类。国内的地震处理软件常用走时定位法进行地震定位。走时定位方法具有以下特点：①震相到时简单、易于拾取，对于近震台站分布密集区域，定位精度可以满足需要，但要求地震台间距较小。据Mori(1991)的研究，只有当最小震中距小于1.4倍震源深度时，基于走时方法确定的震源深度才有较高精度；②对地壳的速度模型较敏感。

PTD定位方法(朱元清，1990)也是走时定位法的一种，常用于定位地震深度。该方法利用在不同震中距的初至震相，将初至Pn震相到时做相应变换，减去初至P波到时测定震源深度。充分利用初至震相，增加资料精度，克服了直达波辅助定位震源深度的缺陷。本文采用华南模型与AH2015地壳速度结构模型(谢石文，2016)，应用PTD深度计算软件和MSDP软件中的单纯型定位法，重新计算2017年安徽区域发生的地震震源深度，旨在研究2种模型对安徽地震震源深度的影响，并分析其适用性。

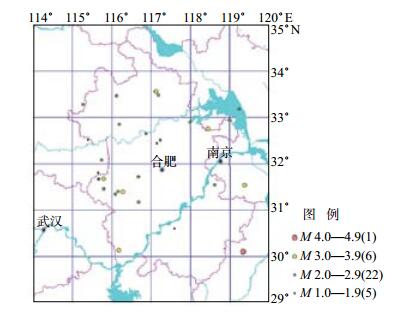
1 资料选取

对于安徽地震台网2017年地震速报及地震目录，从中选取34个安徽及周边地区M_L > 1.5地震，其中5个M_L 1.0—1.9地震，22个M_L 2.0—2.9地震，6个M_L 3.0—3.9地震，1个M_L 4.0以上地震。所选地震震中分布均匀，覆盖安徽省大部分区域，震中分布见图 1。

2 PTD方法原理

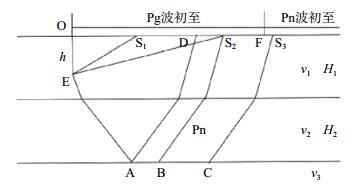
假定地壳为一个均匀地二层速度模型，见图 2，图中E表示震源，h表示震源深度，O表示震中，S₁、S₂、S₃表示3个震中距不同的台站，H₁、H₂和v₁、v₂分别为地壳中第1层、第2层的厚度与P波速度，v₃表示上地幔顶部Pn波速度，A点为Pn波在莫霍面的临界出射点，D点表示Pn波在地表的临界出射点，F为Pg和Pn波的交汇点。

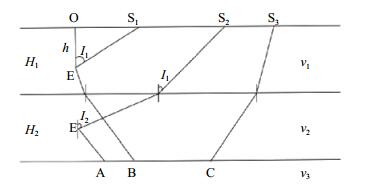
假设某地震在S₂台站上记录到初至Pg波，在S₃台站上记录的初至震相为Pn波，将S₃台站记录的Pn波初至到时减去在莫霍面上滑行BC所用走时，得到由S₃台站转换到S₂台站的Pn转换到时；减去S₂台站的Pg波到时，得到折合走时后Pn与Pg波走时差，结合理论模型计算二者走时差，即可得到震源深度。当S₁台站的震中距小于Pn波的临界出射震中距OD时，将S₃台站的Pn波减去Pn波在AC段的滑行时间，并转换到虚拟台站D处，减去S₁点的Pg波到时，同样可以确定震源深度。二层速度模型下不同震源深度的射线示意见图 3。

假设地壳速度结构为n层均匀模型，H为震源深度，H_i为各层厚度，v_i为各层速度，I_i为各层折射角，当$\sum\limits_{i = 1}^{n - 1} {} {\rm{ }}{H_i} < H \le \sum\limits_{i = 1}^{n - 1} {} {\rm{ }}{H_i} $时，则各层直达波Pg的震中距和走时计算公式为

$ \left\{ \begin{array}{l} \mathit{\Delta} \sum\limits_{n = 1}^{n - 1} {} {H_i}{\rm{ tan}}{I_i} + \left({H - \sum\limits_{n = 1}^{n - 1} {{H_i}} } \right){\rm{tan}}{I_n}\\ T = \sum\limits_{i = 1}^{n - 1} {} \frac{{{H_i}}}{{{v_i}\cos {I_i}}} + \frac{{H - \sum\limits_{i = 1}^{n - 1} {{H_i}} }}{{{v_n}\cos {I_n}}} \end{array} \right. $

(1)

Pn波同样可以写成走时通式，则

$ \left\{ \begin{array}{l} {T_{{\rm{Pn}}}} = \frac{{2{H_n} + \sum\limits_{i = 1}^{n - 1} {{H_i}} - H}}{{{u_n}}} + \sum\limits_{i = 1}^{n - 1} {\frac{{{H_i}}}{{{u_i}}}} + \frac{\mathit{\Delta} }{{{v_{n + 1}}}}\\ {u_i} = \frac{{{v_{n + 1}}{v_i}}}{{\sqrt {v_{n + 1}^2 - v_i^2} }} \end{array} \right. $

(2)

在计算深度—走时差时，对于给定的速度结构，利用Snell定律，求解震源在地表时Pn波临界反射到地表的震中距，则

$ \mathit{\Delta} d = 2\sum\limits_{i = 1}^n {} {H_i}{\rm{tan}}{I_i} $

(3)

其中：I满足$\frac{{\sin {I_i}}}{{{v_i}}}{\rm{ = }}\frac{1}{{{v_{n + 1}}}} $。将Pn到时进行变换，减去相应的Pg初至到时，对震中距小于Δd的台站，有

$ \Delta {T_{ij}} = T_{{\rm{Pn}}}^i - \frac{{\mathit{\Delta} _{{\rm{Pn}}}^i - \mathit{\Delta} d}}{{{v_n}}} - T_{\rm{P}}^i $

(4)

当台站震中距大于Δd时，走时差为

$ \Delta {T_{ij}} = T_{{\rm{Pn}}}^i - \frac{{\mathit{\Delta} _{{\rm{Pn}}}^i - \mathit{\Delta} _{{\rm{Pg}}}^j}}{{{v_n}}} - T_{\rm{P}}^i $

(5)

其中：i表示第i个Pn震相，j表示第j个Pg震相，$\mathit{\Delta} _{{\rm{Pn}}}^i $和$ \mathit{\Delta} _{{\rm{Pg}}}^j $分别表示其震中距。由式(4)、式(5)求得走时差$ \mathit{\Delta} {T_{ij}}$，根据相应震中距$\mathit{\Delta} _{{\rm{Pg}}}^j $，查表得到深度值，对i个Pn震相和j个Pg震相，查表得到i×j个深度值；进行适当取舍与加权平均，最终确定地震的震源深度。采用均匀分层模型可能出现双解，因不同震中距上同一深度的走时差不一致，只需利用2个不同的Pg震相即可解决。因此，确定震源深度至少需要1个Pn震相和2个Pg震相。

据PTD原理可知，地壳速度结构模型对于震源深度计算较重要。文中涉及2种地壳速度模型，分别为华南模型(范玉兰，1990)与2015年建立的适用于安徽区域的AH2015速度模型。2种模型参数见表 1。

3 震源深度定位结果

选取2017年安徽及附近地区发生的34次地震，经中国地震台网中心地震编目库提取震相观测报告及震相走时数据，运用控制变量法，保证震相走时数据不变，配置华南模型与AH2015模型，使用PTD定位程序与单纯型定位法进行重新定位，统计并对比分析每个地震的震源深度。

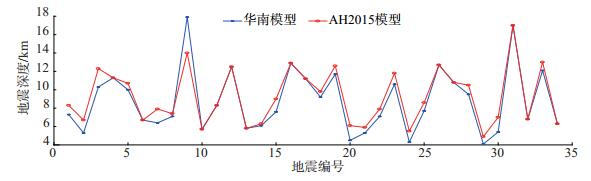
3.1 PTD定位结果

使用PTD方法，对所选34次地震，分别配置华南模型与AH2015模型，定位深度对比结果见图 4，可见：①配置华南模型时，所选地震平均深度为8.75 km，均方差为3.45 km；配置AH2015模型时平均深度为9.24 km，均方差为3.03 km，深度分布更加集中。可见，因AH2015模型的P波速度与地壳厚度比华南模型大，配置该模型时，安徽地震定位深度略大；②地震编号9、31分别对应2017年8月5日河南固始、2017年2月14日江苏宝应地震，因位于安徽省界以外，台站包围较差，地震定位深度较大。

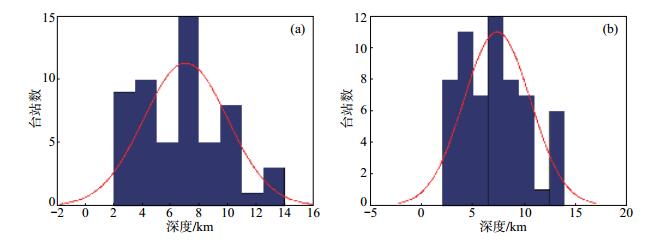
以2017年8月26日安徽霍山M 2.7地震为例，选择不同数量的定位台站，分别配置华南模型与AH2015模型，采用PTD方法进行深度定位，结果见图 5。由图 5可见：①配置华南模型时最优定位深度为7.1 km，配置AH2015型时最优深度为7.4 km，二者相差不大；②若震源深度定位在6 km、9 km左右，配置AH2015模型时，参与深度定位的地震台站较多；③配置AH2015模型时，震源深度较集中，且所选地震深度在6—10 km范围内，说明该模型更加符合安徽区域实际地壳结构，对该区域地震的深度定位更加准确，且台站较少时也能较好地定位地震深度。

3.2 单纯型法定位结果

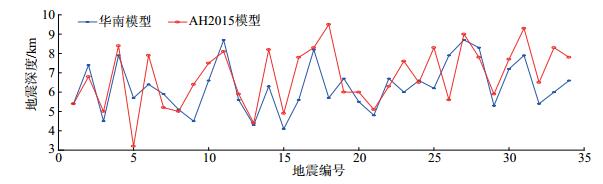
按照同样思路，使用单纯型定位方法，分别配置华南模型与AH2015模型，对所选34次地震重新定位，深度定位结果见图 6。由图 6可知，配置华南模型的定位深度平均6.29 km，均方差为1.27 km；配置AH2015模型的定位深度平均6.81 km，均方差为1.54 km。对比图 4可知，相对PTD定位方法，单纯型定位法对地壳模型的依赖程度较小，定位深度更加稳定、集中。

3.3 单个地震定位结果

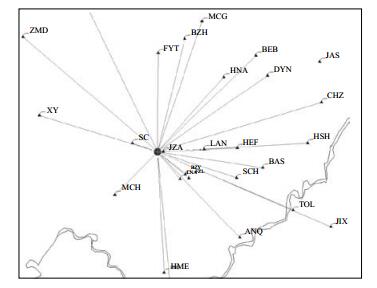
震源深度定位，除地壳速度结构模型，还受到台站包围度、参与定位的震相以及台站与地震的距离等因素的影响。因此，为了研究地壳速度结构模型对震源深度定位的影响，其他因素需保持不变。为保证定位结果更加准确，选取安徽境内发生的地震，该区台站密度大且包围度较好。以2017年4月29日安徽金寨M 3.1地震为例，采用PTD及单纯型定位方法，配置华南模型与AH2015模型，对比所得震源深度，结果见表 2。据中国地震台网中心地震目录，此次M 3.1地震震中为(115.79°E，31.68°N)，深度为7.7 km，震中位置及台站射线路径见图 7(最小震中距8.81 km，最大震中距269.26 km)。

由表 2、图 7可知：①配置AH2015模型时深度定位结果略大；②PTD及单纯型定位方法对不同模型所得定位深度差分别为1.9 km、2.3 km；③使用PTD方法定位时，远台参与定位所得震源深度比近台参与时大。

4 结论

对2017年发生于安徽及周边区域M_L 1.5以上地震，使用PTD方法与单纯型定位法，分别配置华南模型与AH2015模型进行重新定位，研究选用不同地壳速度结构模型对安徽区域地震深度的影响，可以得到以下结论：①配置AH2015模型时，定位深度普遍较大；②配置AH2015模型时定位深度分布更加集中、稳定；③对于单个地震定位，配置AH2015模型时，定位结果显示，接近实际地震深度的台站较多，可见AH2015模型更加符合安徽区域实际地壳结构；④对于台站包围不好的地震，配置2种模型，定位深度均可能出现畸变；⑤单纯型定位法是一种搜索算法，配置2种模型时定位结果相差不大，震源深度分布集中、稳定，且对于包围不好的地震，定位深度依然较为稳定；⑥单纯型法对地壳速度结构模型的依赖程度较小，而PTD定位方法采用平坦的二层地壳模型，利用初至震相可增加定位精度，对地壳速度结构敏感性较高。

AH2015模型对于安徽区域地震深度定位比华南模型更加稳定、可靠，可用于该区域的地震速报与编目。