2. 中国甘肃 730046 兰州地球物理国家野外科学观测研究站;
3. 中国甘肃 730000 中国地震局兰州地震研究所
2. Lanzhou National Geophysics Filed Science Research Station, Gansu Province 730046, China;
3. Lanzhou Institute of Seismology, China Earthquake Administration, Gansu Province 730000, China
地球分为地壳、地幔和地核3部分,地壳与地幔的分界面叫莫霍面,地幔与地核的分界面叫古登堡面。我国陆地下莫霍面总体呈西边厚东边薄的趋势,西部地区莫霍面最深部位可以达到70 km,而东部平原及沿海地区平均深度30 km左右。莫霍面在我国陆表下呈倾斜状,文中称为倾斜界面。当传播路径较短时,受地球曲率的影响较小,通常将地球表面及各层界面看作平层界面,此为理想化界面。
地球内部的物理形态不一,地震波的表现也不一样,由震源发出,经过界面反射后的波是反射波,记录较好的反射波是经莫霍界面反射的PMP波、SMS波。地震波及其走时曲线对地震监测和地震勘探具有重要意义。通过研究倾斜界面反射地震波走时以及不同深度地震波的走时曲线,可以计算震源深度,更好地研究地震波性质及其在地壳中的速度分布。
由于地球内介质分布复杂,地震波在传播过程中会遇到各种介质界面,波在各层中速度变化也不一样,一般波速随着深度的增加而逐渐递增。从传播路径角度,地震波走时是地震波从震源传播到观测点所用的时间。描述地震波走时规律的核心是走时方程,其表达了地震波走时与地震波传播路径之间的关系。地震波的速度随着深度的变化而变化。莫霍面是高速间断面,当地震波传播到该界面时,波射线会出现曲率加大现象,走时曲线出现回折圈。针对倾斜界面地震波传播的走时曲线和传播特性等,可采用多种方法进行研究(孙章庆等,2010),正演是其中的有效途径。本文根据不同震中距、不同倾角地震波在平层界面和倾斜界面的走时曲线,来分析地震波传播特点。
1 计算公式基于射线理论,采用地震波动方程,分别对平层界面与倾斜界面反射波进行数值模拟。
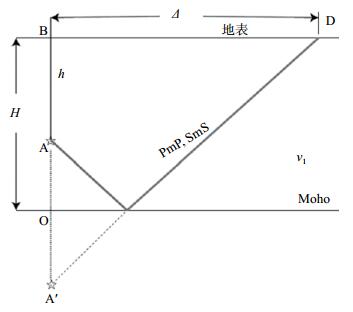
1.1 平层界面反射波赵爱华等(2006)假设莫霍面深度为H,震源深度为h和震中距为Δ(图 1),根据初等几何知识,可知反射波走时为
| $ {t_{{\rm{PmP, SmS}}}} = \frac{{\sqrt {{\mathit{\Delta} ^2} + {{(2H - h)}^2}} }}{v} $ |
|
图 1 反射波路径示意 Fig.1 Reflected wave path diagram |
假设地壳厚度为30 km,震源深度为8 km,SMS波速度为3 km/s,PMP波速度可按Possion体计算,则可采用以下程序模拟平层界面反射波走时。
h=8;H=30;vs=3;vp=vs*sqrt(3); x=0:1:200;
tpmp=sqrt(x.*x+(2*H-h)*(2*H-h))/vp; tsms=sqrt(x.*x+(2*H-h)*(2*H-h))/vs;
tpa=x/vp; tsa=x/vs; plot(x, tpmp, 'b', x, tsms, 'r', )
xlabel('震中距/km') ylabel('走时/s')
set(gca, 'box, "on') ylim([0 70])
legend('PMP波', 'SMS波, "location', 'NorthWest')
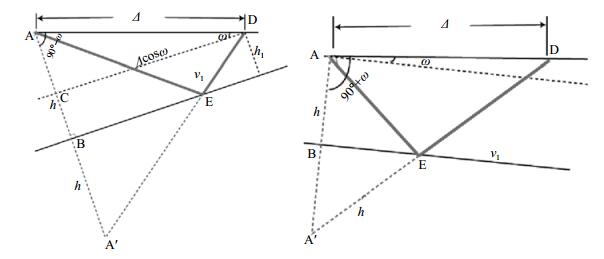
1.2 倾斜界面反射波若2种均匀介质的分界面与地平面夹角为ω,震源在地表,与斜面距离为h,以倾斜界面为对称线,找到震源A点的对称点A′,则AE=A′E,根据反射定律,要求A′ED在一条直线上(图 2),因此,反射总路径AE+ED=A′D(万永革,2016)。
|
图 2 倾斜界面反射波路径 Fig.2 Reflected wave path of inclined interface |
由于界面CD与倾斜界面平行,在三角形ACD中,∠ACD为直角,∠BAD=90°±ω(负号表示地震波上行,正号表示地震波下行),则在三角形AA′D中,根据余弦定理,有
| $ \begin{array}{l} A'D = \sqrt {A'A + {\rm{ }}A{D^2}{\rm{ - 2 }}A{\rm{ '}}A \cdot AD \cdot \cos \left({\angle BAD} \right){\rm{ }}} {\rm{ = }}\\ \sqrt {4{h^2} + {\mathit{\Delta} ^2} - 4h\Delta \cos \left({90^\circ \pm \omega } \right)} = \sqrt {4{h^2} + {\mathit{\Delta} ^2} \pm 4h\Delta \sin \omega } \end{array} $ |
则倾斜界面PMP波、SMS波走时为
| $ t = \frac{{A'D}}{{{v_1}}} = \frac{{\sqrt {4{h^2} + {\Delta ^2} \pm 4h\mathit{\Delta} \sin \omega } }}{{{v_1}}} $ |
式中,负号表示地震波上行,正号表示地震波下行。
2 走时计算震源深度相同而界面倾斜角度不同(5°、10°、15°、20°)时,分别在地震波上行和下行2种情况下计算倾斜界面和平层界面的地震波走时,绘制PMP波、SMS波在2种界面的走时曲线。
2.1 地震波上行假设震源深度h = 30 km,PMP波速度为5 km/s,地震波上行,当界面倾斜角度分别为5°、10°、15°、20°时,或者倾斜界面倾角为30°和60°,分别计算倾斜界面和平层界面时的地震波走时。
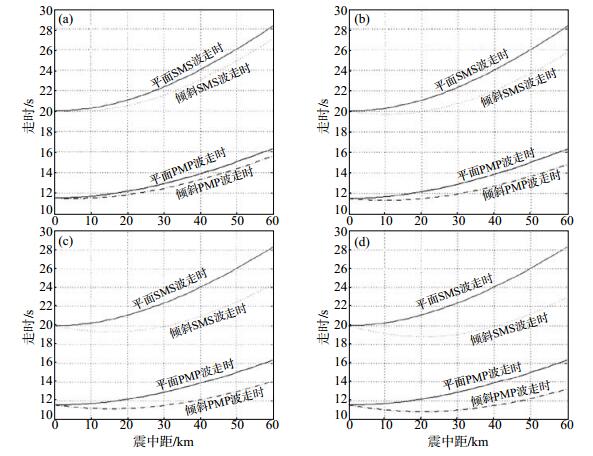
(1)设震中距为0-60 km,当界面倾斜角度分别为5°、10°、15°、20°时,利用Matlab程序,编程绘制PMP波、SMS波走时曲线,见图 3。
|
图 3 不同倾角地震波上行时PMP、SMS波走时曲线 (a)倾斜界面倾角为5°;(b)倾斜界面倾角为10°;(c)倾斜界面倾角为15°;(d)倾斜界面倾角为20° Fig.3 Travel-time curves of PMP and SMS waves at different dips |
Matlab程序如下。
h=30;vs=3;vp=vs*sqrt(3);w=5; x=0:1:60;(w=10, w=15, w=20)tpmp=sqrt(x.*x+4*h*h-4*h*x*sind(w))/vp; tsms=sqrt(x.*x+4*h*h-4*h*x*sind(w))/vs;
thpmp=sqrt(x.*x+4*h*h)/vp; thsms=sqrt(x.*x+4*h*h)/vs;
plot(x, tpmp, 'b-.', x, tsms, 'r:', x, thpmp, 'b', x, thsms, 'r')
xlabel('震中距/km') ylabel('走时/s') set(gca, 'box', 'on') grid on;
legend('倾斜PMP波走时', '倾斜SMS波走时', '平面PMP波走时', '平面SMS波走时', 'location', 'NorthWest')
由图 3可见,地震波上行时,当震中距为0-60 km时,平层界面中PMP、SMS走时随震中距增大而增大,倾角增大时走时变化不大;倾斜界面中PMP、SMS走时随震中距增大而减小,倾角增大时走时减小。2种界面斜率均随倾角增大而减小(匡斌,2005)。因此,倾斜界面地震波上行时,反射波走时公式可化为
| $ t = \frac{{\sqrt {\mathit{\Delta}\left({\mathit{\Delta} - 4h \sin \omega } \right) + 4{h^2}} }}{{{v_1}}} $ |
当Δ<4hsinω时,括号中为负值,则震中距增大,导致分子值减小,PMP波、SMS波走时随震中距增大而减小。
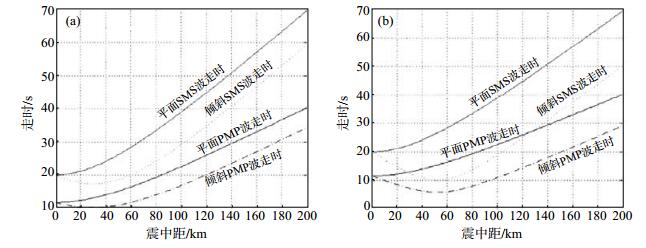
(2)假设震中距为0-200 km,倾斜界面倾角为30°和60°,利用Matlab程序,编程绘制地震波上行时的PMP波、SMS波走时曲线,见图 4。
|
图 4 震中距为0—200 km时不同倾角地震波上行时PMP、SMS波走时曲线 (a)倾斜界面倾角为30°;(b)倾斜界面倾角为60° Fig.4 Travel time curves of PMP and SMS waves with different dip angles when epicenter distance is 0-200 km |
Matlab程序如下。
h=30;vs=3;vp=vs*sqrt(3);w=30; x=0:1:200;
tpmp=sqrt(x.*x+4*h*h-4*h*x*sind(w))/vp; tsmp=sqrt(x.*x+4*h*h-4*h*x*sind(w))/vs;
thpmp=sqrt(x.*x+4*h*h)/vp; thsms=sqrt(x.*x+4*h*h)/vs;
plot(x, tpmp, 'b-.', x, tsms, 'r:', x, thpmp, 'b', x, thsms, 'r')
xlabel('震中距/km') ylabel('走时/s') set(gca, 'box', 'on') grid on;
legend('倾斜PMP波走时', '倾斜SMS波走时', '平面PMP波走时', '平面SMS波走时', 'location', 'NorthWest')
由图 4可见,在震中距在0-200 km时,平层界面的PMP、SMS波随着震中距和倾角的增加,走时曲线基本平行向前且斜率基本相同;倾斜界面中,当倾角不断增加时,地震波走时会随着震中距增加而减小,相同时间内随着倾斜界面倾角的增大,地震波传播的距离减小。
2.2 地震波下行假设震源深度h = 30 km,PMP波速度为5 km/s,地震波下行,当界面倾斜角度分别为5°、10°、15°、20°时,或者倾斜界面倾角为30°和60°,分别计算倾斜界面和平层界面时的地震波走时。
假设震中距为0-60 km,当界面倾斜角度分别为5°、10°、15°、20°时,利用Matlab程序,编程绘制PMP波、SMS波走时曲线,见图 5。
|
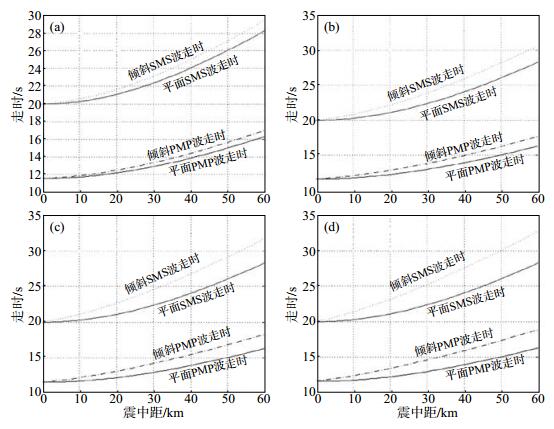
图 5 不同倾角地震波下行时PMP、SMS波走时曲线 (a)倾斜界面倾角为5°;(b)倾斜界面倾角为10°;(c)倾斜界面倾角为15°;(d)倾斜界面倾角为20° Fig.5 Travel-time curves of PMP and SMS waves with different dips in downward seismic waves |
Matlab程序如下。
h=30;vs=3;vp=vs*sqrt(3);w=5; x=0:1:60;(w=10, w=15.w=20)
tpmp=sqrt(x.*x+4*h*h+4*h*x*sind(w))/vp; tsms=sqrt(x.*x+4*h*h+4*h*x*sind(w))/vs;
thpmp=sqrt(x.*x+4*h*h)/vp; thsms=sqrt(x.*x+4*h*h)/vs;
plot(x, tpmp, 'b-.', x, tsms, 'r:', x, thpmp, 'b', x, thsms, 'r')
xlabel('震中距/km') ylabel('走时/s') set(gca, 'box', 'on') grid on;
legend('倾斜PMP波走时', '倾斜SMS波走时', '平面PMP波走时', '平面SMS波走时', 'location', 'NorthWest')
由图 5可见,地震波下行时,震中距为0-60 km,平层界面中PMP、SMS走时随着震中距增大而增大,倾角增大时走时变化不大;倾斜界面中PMP、SMS走时随着震中距增大而增大,倾角增大时走时减小。倾斜界面地震波走时曲线比平层界面地震波走时曲线传播距离小(潘纪顺等,2006)。2种界面斜率均随倾角增大而减小。
假设震中距为0-200 km,倾斜界面倾角为30°和60°,利用Matlab程序,编程绘制地震波下行时的PMP波、SMS波走时曲线,见图 6。
|
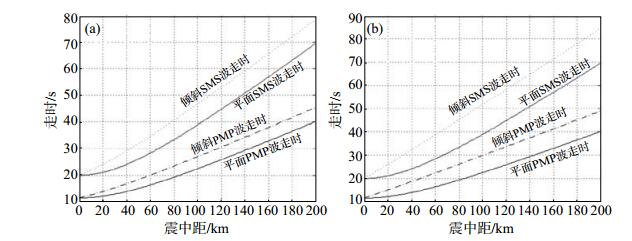
图 6 震中距为0—200 km时不同倾角地震波下行时PMP、SMS波走时曲线 (a)倾斜界面倾角为30°;(b)倾斜界面倾角为60° Fig.6 Travel time curves of PMP and SMS waves with different dip angles when epicenter distance is 0-200 km |
Matlab程序如下。
h=30;vs=3;vp=vs*sqrt(3);w=30; x=0:1:200;
tpmp=sqrt(x.*x+4*h*h+4*h*x*sind(w))/vp; tsms=sqrt(x.*x+4*h*h+4*h*x*sind(w))/vs;
thpmp=sqrt(x.*x+4*h*h)/vp; thsms=sqrt(x.*x+4*h*h)/vs;
plot(x, tpmp, 'b-.', x, tsms, 'r:', x, thpmp, 'b', x, thsms, 'r')
xlabel('震中距/km') ylabel('走时/s') set(gca, 'box', 'on') grid on;
legend('倾斜PMP波走时', '倾斜SMS波走时', '平面PMP波走时', '平面SMS波走时', 'location', 'NorthWest')
由图 6可见,震中距为0-200 km,平层界面的PMP、SMS波随着震中距和倾角的增加,走时曲线基本平行向前且斜率基本相同;倾斜界面中,当倾角不断增加时,地震波走时会随着震中距增加而增大,相同时间内随着倾斜界面倾角的增大,地震波传播的距离反而减小。
2.3 小结由倾斜界面和平层界面中地震波上行和下行的走时曲线可知,在倾斜界面和平层界面中,随震中距和倾角的增大,反射波走时曲线呈平行向前传播,斜率越来越接近。
3 结论通过对比倾斜界面和平层界面PMP、SMP波走时曲线,发现2种界面地震波走时不同,且倾斜界面的倾角对地震波走时有较大影响。在平层界面中,无论上行还是下行地震波,反射波走时随震中距增大而增大,倾角增大时走时变化不大。在倾斜界面中,地震波上行或者下行时,走时随倾角增大而减小。地震波在倾斜界面和平层界面反射,随震中距和倾角的增大,反射波走时曲线斜率越来越小,最后平行向前传播。因此,根据地震波走时曲线可以判断地震波在何种界面传播,并可判断倾斜界面的倾角大小。
| 匡斌, 王华忠, 季玉新, 等. 任意复杂介质中主能量法地震波走时计算[J]. 地球物理学报, 2005, 48(2): 394-398. DOI:10.3321/j.issn:0001-5733.2005.02.023 | |
| 潘纪顺, 张先康, 赵成斌, 等. 二维复杂介质中地震波走时和射线的计算方法及其应用[J]. 地震研究, 2006, 29(3): 245-250. DOI:10.3969/j.issn.1000-0666.2006.03.007 | |
| 孙章庆, 孙建国, 韩复兴. 复杂地表条件下快速推进法地震波走时计算[J]. 计算物理, 2010, 27(2): 281-286. DOI:10.3969/j.issn.1001-246X.2010.02.018 | |
| 万永革. 地震学导论[M]. 北京: 科学出版社, 2016: 195-247. | |
| 赵爱华, 张美根, 丁志峰. 横向各向同性介质中地震波走时模拟[J]. 地球物理学报, 2006, 49(6): 1762-1769. DOI:10.3321/j.issn:0001-5733.2006.06.024 |
 2019, Vol. 40
2019, Vol. 40
