2016年6月23日河北张家口市尚义县(40.95°N,114.20°E)发生M 4.0地震,震源深度14 km,距张北M 6.2地震震中约18 km,距北京260 km。此次地震发生后,国家强震动台网中心接收到7组强震动记录事件,其中河北省地震局4组、内蒙古自治区地震局3组,距震中33.5 km处的怀安新坝房台站记录到最大峰值加速度。
张家口地区位于河北省西北部,京晋冀蒙交界地带,属环首都圈地区,地处晋冀蒙地震危险区范围(李姜等,2017),每次破坏性地震均备受关注,有必要分析张家口地区强震动记录时频特性,为地震波传播规律、作用机理等研究打下基础,也为地震预警提供必要的前提条件(李小军等,2008;李大虎等,2012)。
近年来,地震工程界采用傅里叶变换、小波分析和HHT分析来处理地震加速度记录,而以上方法均存在一定不足,如Fourier变换无法进行时频局部化分析、小波变换对基函数的选取不定等问题,而HHT方法在EMD分解过程中会存在模态混叠问题(罗奇峰等,2003;石春香等,2003)。因此,使用基于聚类经验模态分解(Ensemble Empirical Mode Decomposition,简写为EEMD)的HHT计算方法(Wu et al,2004, 2009;Huang et al,2008),对张家口尚义M 4.0地震强震动记录进行时频特性分析,对比研究不同强震动台记录分量的加速度时程、FFT谱与边际谱、瞬时能量谱以及时频谱等特性,并结合其他类型地震(涿鹿M 4.3地震、九寨沟M 7.0地震)的时频特性,得到一些新的认识及规律。
1 计算方法为避免模态混叠现象,采用基于聚类经验模态分解(EEMD)的HHT计算方法,提取更多地震动时频特性。HHT方法(Hilbert-Huang Transform)是由Huang等(1998)提出的信号处理方法,具有较强的抗噪声能力,能更好地反映信号的本质特征。该方法包含2大部分:聚类经验模态分解(EEMD)(Wu et al,2004, 2009)和Hilbert谱分析(李大虎等,2012b)。聚类经验模态(EEMD)分解方法(李大虎等,2012)为,当附加的白噪声均匀分布在整个时频空间时,该时频空间就由滤波器组分割成的不同尺度成分组成。对于每次EMD分解,添加的白噪声在整个时频空间是均匀分布的,信号的不同频率尺度被自动投影到由白噪声所建立的均匀时频空间的相应频率尺度上。由于每次EMD分解添加不同的白噪声,噪声之间不相关,因此对所有EMD分解的相应IMF求整体平均后,人为添加的噪声被抵消。全体均值被认为是真正的结果,唯一持久稳固的部分是信号本身。
EEMD分解得到不同的各个IMF分量,然后对分解出来的IMF分量进行Hilbert变换,得式(1)(Huang et al,1998;Rilling et al,2003;Huang et al,2008)。Hilbert变换可以有效提取包络、高频调制信号的频率等。
| $ {\hat c_i}\left(t \right) = {c_i}\left(t \right)*\frac{1}{{{\rm{ \mathsf{ π} }}t}}\int_{ - \infty }^{ + \infty } {{c_i}\left({t'} \right)} \frac{1}{{{\rm{ \mathsf{ π} }}\left({t - t'} \right)}}\int_{ - \infty }^{ + \infty } {{c_i}\left({t - t'} \right)} \frac{1}{{{\rm{ \mathsf{ π} }}t'}}{\rm{d}}t $ | (1) |
构造原信号的解析信号,得
| $ {z_i}\left(t \right) = {c_i}\left(t \right) + i{{\hat c}_i}\left(t \right) = {a_i}\left(t \right){{\rm{e}}^{j{\theta _i}\left(t \right)}}\;\;\;\;\;\;\;\;\left(j 为虚数单位 \right) $ | (2) |
其中:瞬时振幅
| $ {z_i}\left(t \right) = {c_i}\left(t \right) + i{{\hat c}_i}\left(t \right) = {a_i}\left(t \right){{\rm{e}}^{j{\theta _i}\left(t \right)}} = {a_i}\left(t \right){{\rm{e}}^{j\int_0^T {{\omega _i}\left(t \right){\rm{d}}t} }} $ | (3) |
| $ x\left(t \right) = \sum\limits_{i = 1}^n {{c_i}\left(t \right)} = {\mathop{\rm Re}\nolimits} \sum\limits_{i = 1}^n {{z_i}\left(t \right)} = {\mathop{\rm Re}\nolimits} \sum\limits_{i = 1}^n {{a_i}\left(t \right){{\rm{e}}^{j{\theta _i}\left(t \right)}}} = {\mathop{\rm Re}\nolimits} \sum\limits_{i = 1}^n {{a_i}\left(t \right){{\rm{e}}^{j\int_0^T {{\omega _i}\left(t \right){\rm{d}}t} }}} $ | (4) |
Hilbert谱表示信号幅值在整个频率段上随时间和频率的变化规律,即
| $ H\left({\omega, t} \right) = {\mathop{\rm Re}\nolimits} \sum\limits_{i = 1}^n {{a_i}\left(t \right){{\rm{e}}^{j\int_0^T {{\omega _i}\left(t \right){\rm{d}}t} }}} $ | (5) |
Hilbert边际谱表示信号幅值在整个频率段上随频率的变化,相当于傅里叶谱,只是具有更高的频率分辨率。Hilbert边际谱通过对Hilbert谱积分得到,即
| $ h\left(\omega \right) = \int_{ - \infty }^{ + \infty } {H\left({\omega, t} \right)} {\rm{d}}t $ | (6) |
Hilbert瞬时能量谱反映信号能量随时间的变化过程,即
| $ IE\left(t \right) = \int_\infty {{H^2}} \left({\omega, t} \right){\rm{d}}\omega $ | (7) |
河北张家口尚义M 4.0地震发生在鄂尔多斯断块隆起、燕山断隆和山西断陷带3个次级新构造单元交界地带(周江林等,2015),距尚义—平泉断裂约10 km(图 1)。地震发生后,河北强震数字台网接收到4组强震动记录事件,内蒙古强震数字台网接收到3组强震动记录事件,怀安新坝房台站(距震中33.5 km)记录到最大峰值加速度。7组强震动记录参数见表 1,可知强震动记录震中距为30.8—136.4 km,最大峰值加速度为8.2 Gal。
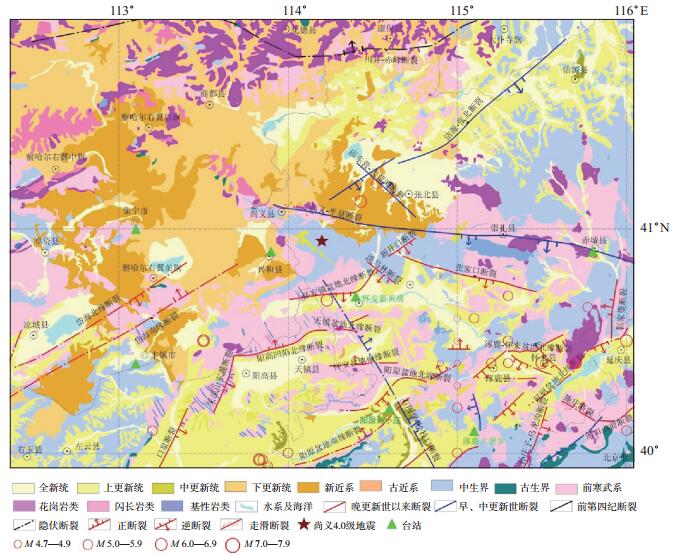
|
图 1 地震地质构造与强震台分布 Fig.1 Seismogeological structure and distribution map of strong motion seismostation |
| 表 1 河北尚义M 4.0地震强震动记录分析 Tab.1 The analysis result of the acceleration recordings of Shangyi M 4.0 earthquake in Hebei |
EEMD分解方法优点在于,可以将分解出来的IMF分量按照频率高低依次提取,地震的强震动记录信息可在图中显现。运用公式(4)—(7),对怀安新坝房台强震动EW分量加速度记录进行计算,得到各IMF分量,C1—C5及res残余项见图 2。由图 2可得以下规律:IMF分量中,C5分量频率最低,C1分量频率最高,随着分量增加,从C2—C3—C4,IMF分量频率逐渐减小,残余项res表示地震加速度曲线的变化趋势,因此,EEMD方法可以将信号自身IMF分量按频率从高到低的顺序提取出来,地震加速度曲线中的信息也可从IMF分量集中体现出来。
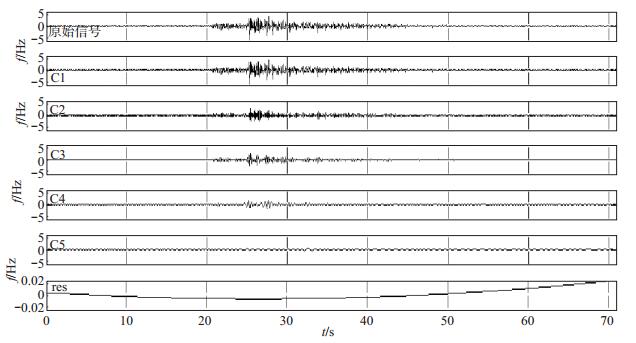
|
图 2 怀安新坝房台强震动EW向各IMF分量(EEMD分解) Fig.2 The IMF components of EW component of strong motion records Huaian-xinbafang station(EEMD decomposition) |
对比分析阳原西小庄台与怀安新坝房台EW分量加速度记录及边际谱和FFT谱,见图 3、图 4。
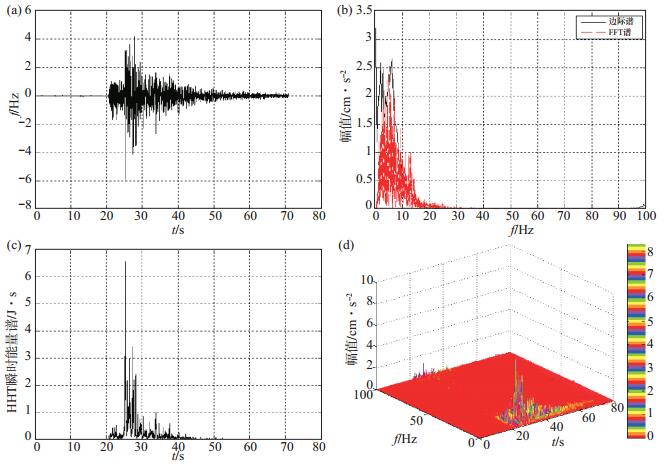
|
图 3 怀安新坝房台强震动记录EW分量加速度时频分析结果 (a)加速度时程记录;(b)边际谱与FFT对比;(c)瞬时能量谱;(d)时频谱 Fig.3 EW component of acceleration time-frequency characteristics analysis at Huaian-Xinbafang station |
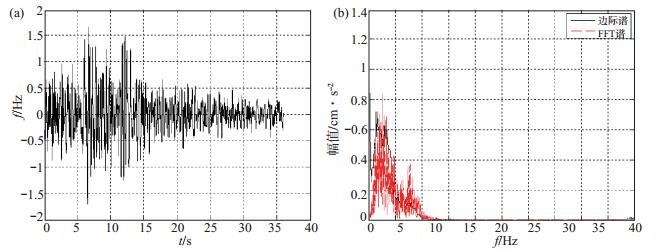
|
图 4 阳原西小庄台强震动记录EW分量加速度时频分析结果 (a)加速度时程记录;(b)边际谱与傅里叶谱对比 Fig.4 EW component of acceleration time-frequency characteristics analysis at Yangyuan-Xixiaozhuang station |
将怀安新坝房台强震仪EW向强震动记录分解的各IMF分量进行Hilbert谱变换,时频分析结果见图 3。由加速度时程记录可知,最大加速度值为6.4 Gal。通过对比边际谱与FFT谱,发现FFT谱的地震动幅值在高频处可放大、低频处可缩小。为验证该规律,对怀安新坝房台强震动NS、UD分量加速度记录以及阳原西小庄台EW分量加速度记录(图 4)进行分解,发现所得结果一致。瞬时能量谱表示能量与时间的变化关系,由图 3(c)可见,25 s前后有一次明显的能量释放过程。
对比图 3、图 4可知,震中距变大,最大地震动峰值加速度逐渐减小,加速度记录主频缓慢增加,在尚义M4.0地震记录中,加速度记录的主频由怀安新坝房台2.0 Hz增加到阳原西小庄台的3.0 Hz。
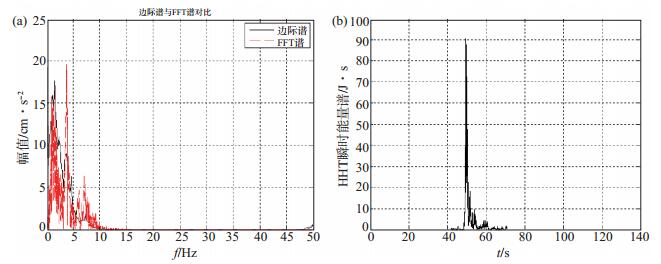
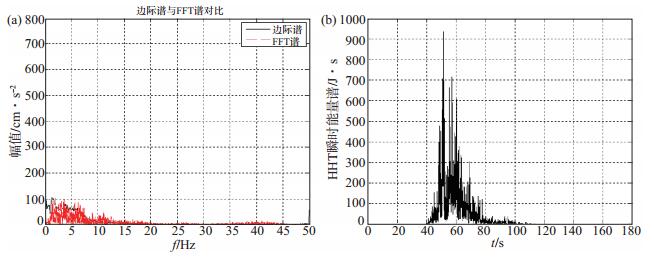
3 震例分析1998年以来,张家口地区先后发生1998年张北M 6.2地震、2014年9月6日涿鹿M 4.3地震、2016年6月23日尚义M 4.0地震,由于国家强震动数据中心无张北M 6.2地震事件强震动记录,在此以涿鹿M 4.3地震为例,选取涿鹿白塔寺台强震动记录EW分量(该台地震动峰值加速度最大,为32.1 Gal),与尚义M 4.0地震怀安新坝房台加速度记录EW分量(图 3)进行对比,研究断层错动类型及发震构造等因素对强震动记录时频特性造成的差异。因2次均为纯走滑型地震,故选取陡倾角左旋走滑型地震(徐锡伟等,2017)——2017年8月8日四川九寨沟M 7.0地震(发震断层为NNW向虎牙断裂北段)强震动记录做对比分析。在此选取九寨白河强震台获取的加速度记录与其他2次强震动记录的EW分量,进行Hilbert变换和谱分析,结果见图 5、图 6。
|
图 5 涿鹿白塔寺台EW向分量加速度时频特性分析结果 (a)边际谱与傅里叶谱对比;(b)瞬时能量谱 Fig.5 EW component of acceleration time-frequency characteristics analysis at Zhuolu-Baitasi station |
|
图 6 九寨百河台EW向分量加速度时频特性分析结果 (a)边际谱与傅里叶谱对比;(b)瞬时能量谱 Fig.6 Time-frequency characteristics analysis of EW component of acceleration at Jiuzhai-Baihe station |
对比图 3、图 5、图 6可知:涿鹿M 4.3、尚义M 4.0地震(纯走滑断层错断引起的地震)(张素欣等,2018)表现为能量集中释放,属孤立型地震;对于九寨沟M 7.0地震(陡倾角左旋走滑型地震),由瞬时能量谱[图 6(b)]可知,在55 s前后有2次明显的能量释放过程。但是通过尚义M 4.0地震[图 3(b)]、涿鹿M 4.3地震[图 5(a)]、九寨沟M 7.0地震[图 6(a)]的FFT谱与边际谱可知,无论是正断层还是逆断层错动,在高频处,FFT谱的地震动幅值大于边际谱的值,也就是说,边际谱与傅里叶谱之间的关系和断层的错动类型关系不大,断层的错断类型对Hilbert瞬时能量谱所反映的信号能量释放特点影响较大。
4 结论运用基于EEMD分解的HHT方法,对河北尚义M 4.0地震不同震中距台站所获取的地震动记录进行时频分析,得到不同分量的加速度记录时程、FFT谱与Hilbert边际谱、瞬时能量谱及时频谱,发现FFT谱的地震动幅值在高频处可放大、低频处可缩小,而断层错动类型、发震构造的不同,与强震动记录时频特点及Hilbert瞬时能量谱所反映的信号能量释放过程之间存在一定关系(李大虎,2012)。
河北省近年发生的中强地震较少,且由于强震台站分布不均匀,导致中强地震发生后,强震动数据记录不完整,建议架设流动强震观测台站,以便及时有效地获取强震动记录,丰富河北省强震动记录数据库,更好地开展强震记录研究,为震后烈度调查、灾后重建提供参考。
论文仅从能量谱的定义出发,对强震动记录造成的破坏进行初步定性分析,具有一定局限性,后续将结合场地条件、构造特征等进行综合研究(吕国军等,2016)。
| 李大虎, 赖敏, 何强, 等. 基于聚类经验模态分解(EEMD)的汶川MS 8.0强震动记录时频特性分析[J]. 地震学报, 2012, 34(3): 350-362. DOI:10.3969/j.issn.0253-3782.2012.03.007 | |
| 李大虎, 梁明剑, 黎小刚, 等. 2011年四川炉霍MS 5.3地震加速度记录的时频分析与能量计算[J]. 西北地震学报, 2012, 34(4): 335-341. DOI:10.3969/j.issn.1000-0844.2012.04.0335 | |
| 李姜, 张合, 周月玲, 等. 河北阳原-蔚县盆地地震灾害损失评估[J]. 华北地震科学, 2017, 35(3): 73-78. DOI:10.3969/j.issn.1003-1375.2017.03.013 | |
| 李小军, 周正华, 于海英, 等.汶川8.0级地震强震动观测及记录初步分析[R].北京: 中国建筑工业出版社, 2008. | |
| 罗奇峰, 石春香. Hilbert-Huang变换理论及其计算中的问题[J]. 同济大学学报, 2003, 31(6): 637-640. DOI:10.3321/j.issn:0253-374X.2003.06.002 | |
| 吕国军, 张合, 孙丽娜. 张家口地区农村房屋抗震性能调查分析研究[J]. 地震工程学报, 2016, 38(Z2): 302-307. DOI:10.3969/j.issn.1000-0844.2016.Supp.2.0302 | |
| 石春香, 罗奇峰. 时程信号的Hilbert-Huang变换与小波分析[J]. 地震学报, 2003, 25(4): 398-405. DOI:10.3321/j.issn:0253-3782.2003.04.007 | |
| 徐锡伟, 陈桂华, 王启欣, 等. 九寨沟地震发震断层属性及青藏高原东南缘现今应变状态讨论[J]. 地球物理学报, 2017, 60(10): 4018-4026. DOI:10.6038/cjg20171028 | |
| 张素欣, 王想, 王亚茹, 等. 河北及邻区地震平静与几次大震的关系[J]. 华北地震科学, 2018, 36(2): 38-42. DOI:10.3969/j.issn.1003-1375.2018.02.006 | |
| 周江林, 尤惠川, 唐方头. 张家口-宣化盆地断裂特征与活动性研究[J]. 地震工程学报, 2015, 37(3): 702-709. DOI:10.3969/j.issn.1000-0844.2015.03.0702 | |
| Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 | |
| Huang N E, Wu Z H. A review on Hilbert-Huang transform:method and its applications to geophysical studies[J]. Reviews of Geophysics, 2008, 46(2): RG2006 | |
| Rilling G, Flandrin P, Gonçalvès P. On empirical mode decomposition and its algorithms[J]//Proceedings of the IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing. Grado, Italy: NSIP, 2003: 1-5. | |
| Wu Z H, Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society of London. Series A:Mathematical, Physical and Engineering Sciences, 2004, 460(2046): 1597-1611. DOI:10.1098/rspa.2003.1221 | |
| Wu Z H, Huang N E. Ensemble empirical mode decomposition:A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. |
 2018, Vol. 39
2018, Vol. 39

 ,
,