军控核查中的一个重要问题是检测和识别核爆,而地震学方法可提供有效识别核爆的手段。因此,应用地震学方法识别小当量核爆已成为重要的科学研究内容,对维护国家利益与保卫世界和平具有重要意义(卢世军,2009)。核爆和地震所产生的振动,均以地震波的形式在介质中进行传播,且二者产生的波形特征相似(刘芳彤等,2015),加之人类活动范围与强度的持续增加对观测数据质量产生的影响,使得正确识别核爆与地震成为地震监测和分析的一项重要挑战。
国内外诸多学者对核爆识别方法进行研究,提出多种地震学识别方法,如:刘希强等(2003)提出利用小波变换能量线性度方法,区分天然地震与爆破或塌方;田有等(2015)通过对比2009年和2013年2次朝鲜核爆的地震学特征,发现在频率大于3 Hz时,利用P/S型谱比值能够有效识别朝鲜地下核爆。由于研究区域的差别以及地震信号的复杂性,以上识别方法尚存不足之处。本文采用小波变换方法,利用Daubechies 8小波变换,对2009—2017年黑龙江省牡丹江地震台(MDJ)记录的5次朝鲜核爆信号进行数据处理,得到精细的近似和细节部分信息,用于研究朝鲜核爆信号波形特征。
1 资料选取黑龙江省牡丹江地震台(下文简称牡丹江台)是国家基准台,地处黑龙江省牡丹江市北郊,地质构造位置位于黑龙江亚板块次一级构造长白块体北部,敦密断裂与牡丹江断裂交汇处。牡丹江台观测环境良好,可为地震研究和防震减灾工作提供基础数据。
2009—2017年黑龙江省牡丹江台记录到5次朝鲜核爆信号,选取震中距、震级与朝鲜核爆差距较小的3次天然地震信号进行对比分析,详细参数见表 1。朝鲜核爆与选取的天然地震能量均较强,波形振幅较大,牡丹江台垂直分量信号记录较好,因此采用8次事件的垂直分量记录进行分析。
| 表 1 5次朝鲜核爆与3次地震参数 Tab.1 Parameters of five North Korea's nuclear explosions and three earthquakes |
1984年地球物理学家Morlet在处理勘探资料时提出小波变换。1989年Mallat在前人研究基础上,将构造小波方法进行统一,提出多分辨率分析概念和二进制小波变换快速算法。
一个函数x(t)的连续小波变换定义(Daubechies,1988;Yong,1993)如下
| $ {W_\tau }\left({a, b} \right)=\frac{1}{{\sqrt a }}\int\limits_{ - \infty }^\infty {x\left(t \right)} g\left({\frac{{t - b}}{a}} \right){\rm{d}}t $ | (1) |
其中,g(t)为窗函数,a为尺度函数,b为滑动函数。与傅里叶变换不同,小波变换使用无限长的正弦信号作为基函数(即小波),公式(1)中所用基函数可迅速衰减为0,且其均值也为0。尺度因子决定小波的拉伸和压缩,低尺度小波变换信号包含原信号中的高频成分,而高尺度小波变换信号包含原信号中的低频成分,不同尺度上的近似信号和细节信号与尺度具有密切关系(杨选辉等,2005;杨军伟等,2012),所以小波分析的优点之一就是处理和分析包含各种频率的地震信号或其他音频信号。
多分辨率是小波分析的一个重要特点。利用小波变换做多分辨率分析,就是将某原始信号分解成不同尺度上的近似信号和细节信号,相当于对该信号分别做带通和低通滤波,进而由粗到细地逐步观察信号。小波变换使用的尺度因子越小,分辨率越高,则反映原始信号的细节信息;使用的尺度因子越大,则主要反映原始信号的低频成分。每进行一次分解,相当于剥离原始信号中部分高频信息,剥离的信息则构成细节信号。小波分析方法的理论基础较为完善,因此,可以选取小波分析方法对核爆与天然地震信号进行分析。
由著名小波分析学者Daubechies构造的小波函数,具有以下特点:①时间域上具有有限支撑;②在频率域上Ψ(ω)在ω处有N阶零点;③Ψ(ω)与其整数位移正交归一,即∫Ψ(t)Ψ(t-k)dt=δk。Daubechies小波无明确表达式,可由尺度函数φt求解。
| $ \mathit{\Psi }\left(t \right) = \sum {{g_k}\varphi \left({2t - k} \right)} $ | (2) |
式中,k取2—2N-1,N值不同,gk值不同。当N = 1时,为Haar小波。本文采用db8小波基对信号进行分解。
3 数据处理 3.1 原始波形特征根据朝鲜核爆与所选地震的发生时刻截取波形数据,运用Matlab,采用db8小波基进行小波变换,将所选信号进行8尺度分解。
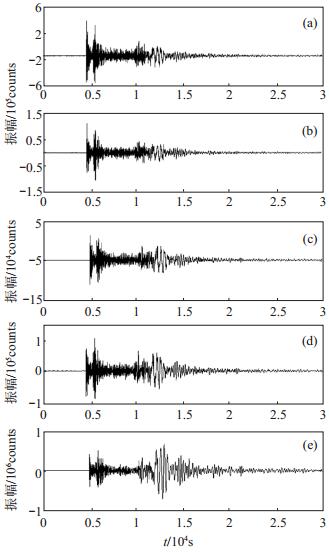
(1)朝鲜核爆。由5次朝鲜核爆原始波形(图 1)可知,朝鲜核爆波形相似度高,均表现为浅源爆炸特征,具体表现为:P波能量较强;Lg波能量较弱;S波较弱;短周期Rayleigh面波能量强等。
|
图 1 5次朝鲜核爆原始波形 (a)2009年朝鲜核爆;(b)为2013年朝鲜核爆;(c) 2016年朝鲜核爆(4.9级);(d)2016年朝鲜核爆(5.0级);(e)2017年朝鲜核爆 Fig.1 The original waveform of five North Korean nuclear explosions |
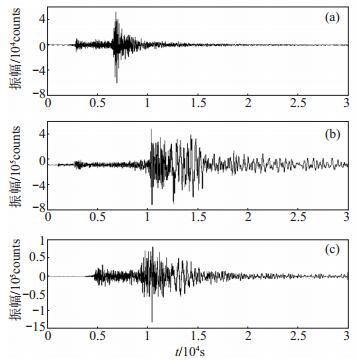
(2)天然地震。3次天然地震原始波形见图 2,可见天然地震波形相似度较高,具体特征为:P波较发育,初动尖锐;S波能量较强,持续时间长,衰减较慢,表现出大周期结尾;面波不发育等。
|
图 2 3次天然地震原始波形 (a)2009年吉林地震;(b)2013年沈阳地震;(c)2017年松源地震 Fig.2 The original waveform of three earthquakes |
对比图 1、图 2可知,朝鲜核爆与天然地震的波形特征有明显不同,可能是由于天然地震为5—20 km岩层中应力从积累到释放的岩石破裂过程,震源机制复杂,地震波经过致密岩层快速传播,能量和高频成分损耗较少,因此天然地震波形复杂且频带较宽,振动持续时间长,振幅和能量衰减慢,高频成分丰富;朝鲜核爆震源一般在几百米至上千米的地表岩层中,为瞬间膨胀源,震源机制简单,地震波经过密度较低的介质传播,能量损耗较多,因此核爆信号频带较窄,震动幅值大,频率高,持续时间短,能量衰减快。
3.2 小波分解对5次朝鲜核爆波形和所选3次天然地震波形进行小波变换分解,得到波形分解后近似部分与细节部分曲线。由于5次朝鲜核爆和3次天然地震波形及小波变换分解后得到的近似部分与细节部分曲线均较为相似,文中仅选取2017年朝鲜核爆与2013年沈阳地震小波变换分解后的近似与细节部分曲线进行分析,见图 3、图 4。
|
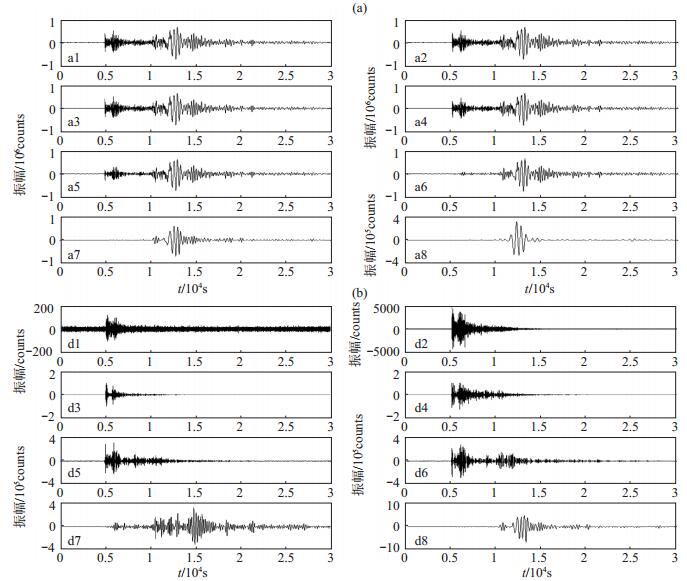
图 3 2017年朝鲜核爆小波分解 (a)近似部分;(b)细节部分 Fig.3 The approximate part and the detail part of wavelet decomposition of North Korean nuclear explosion in 2017 |
|
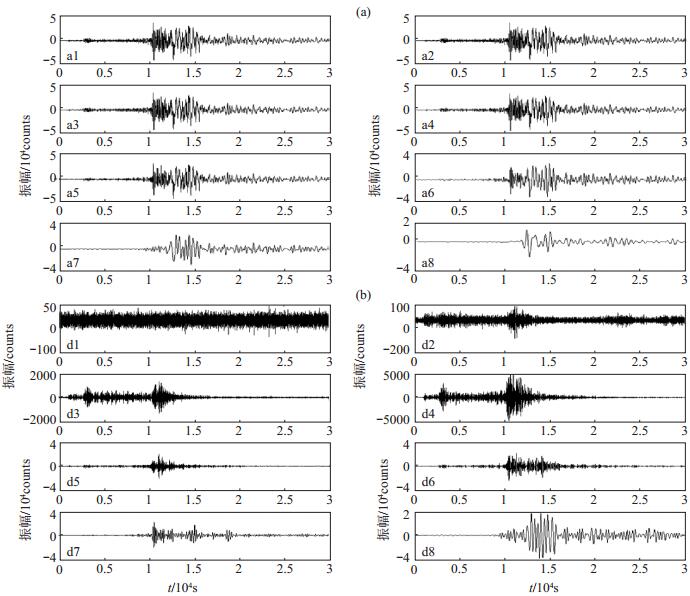
图 4 2013年沈阳地震小波分解 (a)近似部分;(b)细节部分 Fig.4 The approximate part and detail part of wavelet decomposition of Shenyang earthquake in 2013 |
(1)小波变换近似部分。通过对比图 3、图 4中朝鲜核爆和天然地震的小波变换近似部分特征,可知,通过层层剥离高频信息,构建的原始波形近似信号,在1—5阶时曲线特征与原始信号特征基本相同,在6—8阶时高频成分逐渐被剥离,曲线特征出现明显变化,在第6阶近似部分中,朝鲜核爆与天然地震的曲线特征基本相同,在7—8阶时出现明显差异,朝鲜核爆的近似信号变得简单,振幅较大,能量强,衰减较快,而天然地震的近似信号特征与之相反。
(2)小波变换细节部分。高频细节图在低阶中显示,低频细节图在高阶中显示。通过对比朝鲜核爆和天然地震的小波变换细节部分特征可知,朝鲜核爆与所选天然地震小波分解后细节曲线特征不同。由1—4阶细节图可知,天然地震的高频成分较为丰富。随着分解尺度的不断增大,核爆与天然地震能量均在快速衰减。核爆的P波能量大,在1阶细节曲线中明显可见P波波峰,在2—6阶细节曲线中呈现2个波峰,而天然地震P波能量较小且不集中,在1阶细节曲线中波峰被掩盖;核爆信号在分解到第6阶后才呈现面波信息,而天然地震自第2阶起即可见面波信息,且能量较大;核爆信号在分解到第8阶时面波显示清晰,能量因时域范围较窄而集中分布,整段波形较为简单,而天然地震信号在分解到第8阶时面波也较为清晰,但因时域范围较宽,能量分布较不集中,波形比核爆复杂。根据以上特征即可区分朝鲜核爆与天然地震。
4 结束语核爆与地震信号均为非平稳信号,在震源机制、震动频率、持续时间和能量上存在差别。天然地震是在岩石破裂时,岩层中的应力从积累到释放的过程,其震源机制、波形等比较复杂;爆破事件为人工震源,震源机制、波形等较为简单(朱权洁等,2012)。基于小波变换方法对朝鲜核爆与天然地震信号进行逐层分解,提取其波形特征,通过对比、分析实现有效识别,可作为区分核爆与天然地震的一种较好方法。
本文在具体分析时选取2013年沈阳5.1级地震和2017年朝鲜核爆事件进行对比,朝鲜核爆的当量震级为6.3,比地震能量大,且地震和爆炸位置不同,未就“震级”和传播路径差异进行分析,将在今后工作中开展进一步研究。
| 刘芳彤, 杜春鸿. 朝鲜地区地震与爆破波形识别研究[J]. 防灾减灾学报, 2015, 31(2): 58-66. | |
| 刘希强, 沈萍, 张玲, 等. 用小波变换能量线性度方法识别天然地震与爆破或塌方[J]. 西北地震学报, 2003, 25(3): 204-209. DOI:10.3969/j.issn.1000-0844.2003.03.003 | |
| 卢世军.天然地震与人工爆破波形特征提取与识别算法研究[D].桂林: 广西师范大学, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D069900 | |
| 田有, 柳云龙, 刘财, 等. 朝鲜2009年和2013年两次核爆的地震学特征对比研究[J]. 地球物理学报, 2015, 58(3): 809-820. | |
| 杨军伟, 林大能, 艾德春. 基于小波方法的露天矿台阶爆破振动信号分析[J]. 工程爆破, 2012, 18(4): 18-22. | |
| 杨选辉, 沈萍, 刘希强, 等. 地震与核爆识别的小波包分量比方法[J]. 地球物理学报, 2005, 48(1): 148-156. DOI:10.3321/j.issn:0001-5733.2005.01.020 | |
| 朱权洁, 姜福兴, 于正兴, 等. 爆破震动与岩石破裂微震信号能量分布特征研究[J]. 岩石力学与工程学报, 2012, 31(4): 723-730. DOI:10.3969/j.issn.1000-6915.2012.04.011 | |
| Daubechies I. Orthonormal bases of compactly supported wavelets[J]. Communications on Pure and Applied Mathematics, 1988, 41(7): 909-996. DOI:10.1002/(ISSN)1097-0312 | |
| Yong R. Wavelet theory and its applications[M]. Boston: Kluwer Academic Publishers, 1993: 69-74. |
 2018, Vol. 39
2018, Vol. 39
