震源深度是描述震源参数的重要参数之一,与发震时刻、震中位置相互制约。准确的震源深度不仅可以减小发震时刻与震中位置的误差,提供更为精确的地震参数,也可以为发震断层分布及活动性分析等研究提供重要基础(张帆等,2017)。因地下结构未知,缺乏有效约束条件,导致定位深度具有不准确性,从而影响对发震构造、断层活动性及危险性评估的判断。因此,如何利用测震台网现有数据资料进行准确的深度定位是当前测震学研究的重点之一,对于日常工作及科学研究均具有重要意义。
为了提高震源深度的精度,地震学者提出许多深度测定方法,一般为基于走时的定位方法与波形反演方法。目前,S、P震相到时差(刘春等,2009)、同一台站的Pg、Pn震相到时差(Greensfelder et al,1965)、远台初至Pn与近台初至Pg震相到时差组对(朱元清等,1990)等震相到时方法较为常用,但是对台间距、震中距、速度模型等要求较高(郑勇等,2017)。波形反演法包括偏振信息法、振幅信息法与深度震相法,其中深度震相对震中距变化不敏感,对深度变化敏感,可以较好地约束震源深度(罗艳等,2013)。目前使用较多的近震深度震相有sPg、sPmP、sPn以及参考震相Pg、PmP、Pn等,通过测量不同震相之间的到时差以及波形拟合计算震源深度。但是,不同深度震相有其各自优势震中距与适用条件(詹小艳等,2014),如:sPg震相只有在上地壳有较大且光滑的速度梯度时才能发育较好(崇加军等,2010);sPmP适用于结构简单、震源深度较深的地震,sPn类似于首波,初动弱,不易拾取(郑勇等,2017)。崇加军等(2010)提出一种近震深度震相sPL,该震相与P波到时差随震中距几乎不变,但与震源深度成线性关系,且主要出现在震中距50 km范围内,单台观测即可确定震源深度,不仅可为地震台站稀疏的测震台网确定震源深度提供新思路,对于布局较好的测震台网内不同台站观测的sPL震相,可提供相互验证的基础。
2017年9月4日03时04分河北临城地区发生ML 4.4地震,震中位于华北地震带中南部邢台老震区,是该区域自2002年河北隆尧MS 4.8地震发生以来的最大地震。临城地区断裂发育,构造复杂,该区是地震活跃地区。西部为晋获断裂,北部为保定—石家庄断裂,东部为元氏断裂、隆尧断裂(吴鹏等,2017)。因此,明确该地震的震源参数对研究临城地区以及邢台老震区断裂活动性具有重要意义。河北测震台网完整记录了此次地震,且震中附近台站分布较好,为有效提取sPL震相、计算可靠的震源深度提供良好的数据基础。
1 方法原理均匀半空间模型中,自震源出发的SV波入射到自由表面下方时,会有部分能量转换为P波,当入射角大于临界角时,转换P波将沿自由表面传播,称为“Surface P-wave”(Aki et al,2002);而在实际的地球模型中速度会随深度增加,导致入射SV波与转换P波均不是单一震相,而是经过多次反射、折射的复杂震相,由于到时基本一致,转换P波与“Surface P-wave”混合形成新的波列。因为这一波列是由S和P波相互耦合生成,所以将其定义为sPL震相,其传播路径见图 1(崇加军等, 2010, 段刚,2018)。sPL震相仅在较小震中距范围内传播,优势震中距范围为30—50 km,震相特征为:到时介于P波与S波之间,起始没有P波尖锐,高频成分少,径向能量强,即径向振幅最大,垂直向次之,切向较小且基本观察不到(崇加军等,2010)。

|
图 1 均匀半空间下sPL、P波传播路径 Fig.1 Ray path of sPL and P wave for the model of half space |
根据均匀半空间下sPL震相的产生原理(崇加军等,2010),假设P波速度为vP,波速比为vP/vS,震源深度为h,则tsPL-P(sPL与P波到时差)与震中距关系(包丰等,2013)为
| $ {t_{{\rm{sPL}} - {\rm{P}}}} = \frac{{h \times \sqrt {{\alpha ^2} - 1} + \Delta - \sqrt {{h^2} + {\Delta ^2}} }}{{{v_{\rm{P}}}}} $ | (1) |
当震中距远大于震源深度时,则h2 + Δ2相当于Δ2,式(1)可简化为
| $ {t_{{\rm{sPL}} - {\rm{P}}}} = \frac{{\sqrt {{\alpha ^2} - 1} }}{{{v_{\rm{P}}}}} \times h $ |
即当震中距大于
(1) 地壳速度模型。河北临城地区位于华北平原中南部,以西为太行隆起,以东为华北断坳,属于中生代沉积(河北省地质矿产局,1989)。据崇加军等(2010)的研究,对于此类地区,计算sPL理论震相时可选用2层地壳速度模型。王莉婵等(2016)针对河北地区建立一维地壳速度模型,因缺少密度参数,结合crust 2.0模型,作为最终计算理论波形的地壳速度模型(表 1)。
| 表 1 河北一维地壳速度模型 Tab.1 1D crustal velocity model of Hebei |
(2) 震源机制解。利用sPL震相确定震源深度时需要根据震源机制解计算理论波形图。因此,利用矩张量反演方法(TDMT-INV),计算得到临城ML 4.4地震的震源机制解,具体结果见表 2。后续计算采用节面Ⅰ的结果。
| 表 2 河北临城ML 4.4地震震源机制解 Tab.2 Solution of seismic source mechanism of ML 4.4 earthquake in Lincheng, Hebei Province |
为验证此次临城ML 4.4地震是否存在理论sPL震相,且该震相是否可用于判定震源深度,利用F—K方法,基于河北地区一维地壳速度模型(结合crust 2.0模型)及震源机制解,进行以下计算:①固定震源深度、方位角,计算不同震中距的理论震相;②固定震中距、方位角,计算不同震源深度的理论震相。
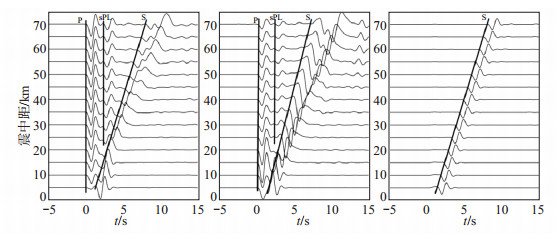
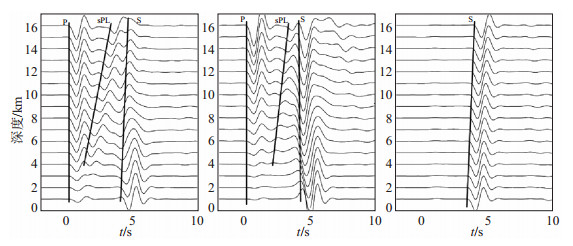
给定震源深度10 km,方位角30°,计算震中距5—70 km范围内理论震相,结果见图 2(由左向右为径向R、垂直向Z、切向T波形)。给定震中距30 km,方位角30°,计算震源深度2—16 km范围内理论震相,结果见图 3(由左向右为径向R、垂直向Z、切向T波形)。
|
图 2 震中距5—70 km范围内理论波形(震源深度10 km,方位角30°) Fig.2 The theoretical waveforms for Δ = 5—70 km (depth=10 km, Azi = 30°) |
|
图 3 震源深度2—16 km范围内理论波形(震中距30 km,方位角30°) Fig.3 The theoretical waveforms for depth = 2—16 km (Δ = 30 km, Azi = 30°) |
由图 2、图 3可见:在径向与垂直向上,P波与S波之间存在明显的低频震相,起始没有P波尖锐,呈低频特征,且该震相垂直向振幅小于径向,切向振幅观察不到,符合sPL震相特征,由此判定该震相为sPL震相;sPL与P波到时差随震中距大小无变化,但随震源深度线性增加,因此,可以利用sPL震相判定临城ML 4.4地震震源深度。
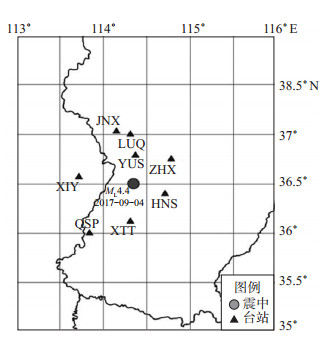
2.3 台站数据据崇加军等(2010)的研究成果,sPL震相在震中距30—50 km范围内发育较好,由图 2可知,此次临城ML 4.4地震理论sPL震相在震中距20 km以上出现,为得到更多有效数据,将震中距范围扩大至20—70 km,得到满足条件的10个地震台(图 4),分别为:YUS(Δ = 31.88 km)、HNS(Δ = 33.84 km)、XTT(Δ = 42.63 km)、ZHX(Δ = 46.95 km)、REX(Δ = 51.45 km)、LUQ(Δ = 55.49 km)、XIY(Δ = 55.73 km)、JNX(Δ = 60.67 km)、TAG(Δ = 61.16 km)、QSP(Δ = 72.34 km)。其中,REX、TAG地震台安装井下短周期地震计,ZHX台安装井下宽频带地震计,其他台站均安装地表宽频带地震计。由于sPL震相表现为低频特征,去除REX、TAG地震台,选用YUS、HNS、XTT、ZHX、LUQ、XIY、JNX、QSP地震台记录数据参与此次地震震源深度计算。所选地震台站及此次ML 4.4地震震中分布见图 4。
|
图 4 临城ML 4.4地震及所选地震台分布 Fig.4 Distribution of Lincheng ML 4.4 earthquake and the stations |
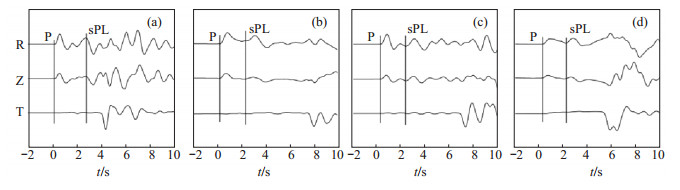
对所选8个地震台记录的波形数据进行处理,将EW向、NS向波形转换为径向(R)、切向(T)记录,与垂直向波形积分至位移记录,去除均值,为观测到清晰的sPL震相,进行1—4 Hz滤波,观察P波与S波之间是否存在sPL震相。经以上处理,发现可在YUS、JNX、LUQ、XTT地震台记录的P波与S波之间观察到较为明显的低频震相,见图 5。由图 5可见,该震相起始没有P波尖锐,呈低频特征,振幅小于P波,且能量主要集中在径向,垂直向次之,切向观察不到,符合sPL震相特征。
|
图 5 4个台站处理波形 (a)YUS台;(b)JNX台;(c)LUQ台;(d)XTT台 Fig.5 The processed waveforms of the 4 stations |
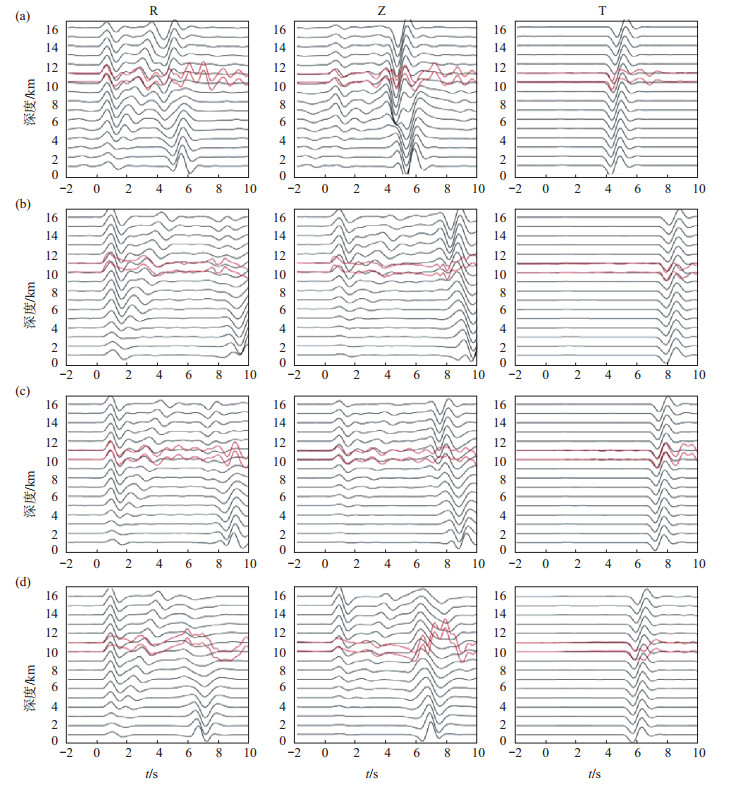
为进一步验证,利用F—K方法,基于河北地区一维地壳速度模型(结合crust 2.0模型)及震源机制解,计算YUS、JNX、LUQ、XTT地震台在震源深度1—16 km范围内的理论波形,并进行1—4 Hz低频滤波,利用P波与sPL震相到时差可约束震源深度的特点(崇加军等,2010),与观测波形进行对比,波形拟合结果见图 6,图中红色曲线为处理后的观测波形,黑色曲线为理论波形,图件从左到右依次R、Z、T波形曲线。
|
图 6 4个台站观测与理论波形三分向拟合对比 (a)YUS台;(b)JNX台;(c)LUQ台;(d)XTT台 Fig.6 The comparison of observered waveforms and theoretical waveforms of the 4 staions |
由图 6可见,当震源深度为10—11 km时,P波及sPL震相理论波形与观测波形拟合较好,可见利用sPL震相判定临城ML 4.4地震震源深度在10—11 km。
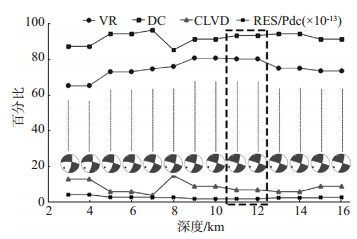
3.2 结果验证(1) 与TDMT-INV结果对比。TDMT-INV方法是,给定震源深度,利用F—K方法计算理论地震波,通过线性最小二乘法,计算理论与观测波形的拟合残差,并使其最小。利用层状速度模型计算理论地震图,震源深度影响较大,从而影响反演的最终结果(林向东等,2013)。震源深度设定在3—16 km范围内,对于同一震源深度,计算临城ML 4.4地震矩张量解中的方差缩减(VR)、纯双力偶源(DC)、补偿线性矢量偶极(CLVD)及残差(RES/Pdc),结果见图 7。由图 7可见,震源深度11—12 km为最佳解,此时VR和DC较大,CLVD和RSE/Pdc最小。因此,本次反演所得震源深度为11—12 km。
|
图 7 临城ML 4.4地震矩张量解中VR、DC、CLVD、RES/Pdc随深度变化 Fig.7 The DC, CLVD component, VR and RES/Pdc iterated with the depth of Lincheng ML 4.4 earthquake moment solution |
(2) 与PTD结果对比。PTD深度测定方法是,利用不同地震台站记录的初至震相(一般为Pg、Pn)到时做变换,组成到时差对计算震源深度。该方法依赖于地壳速度模型,模型越接近实际情况,PTD程序计算结果越可靠(王莉婵等,2016)。
为保证结果的可比性,此次计算采用表 1给出的地壳速度模型,利用PTD方法,重新定位此次临城ML 4.4地震震源深度,深度分布结果见图 8,可见计算结果比较符合高斯分布。因本次计算使用样本3 595个,占样本总数(80个Pg×53个Pn)的84.79%,可见深度计算结果较可靠。利用PTD方法,计算得到最佳震源深度为11.6 km,与利用sPL震相计算所得10—11 km基本一致,表明sPL震相计算结果可信。

|
图 8 PTD计算结果 Fig.8 The PTD result |
(3) 与河北测震台网编目结果对比。由河北地震编目结果可知,临城ML 4.4地震采用JOPENS—MSDP软件中的单纯型定位方法,标注台站118个,震相227个,实际定位采用台站28个,震相56个(Pg、Sg震相各28个),震源深度6 km,与利用sPL震相所得结果存在4—5 km的差值,差异较大。据杨选等(2018)的研究可知,当地震台站布局较好时,MSDP的常用4种定位方法(单纯型、HypoSat、Hyp2000、LocSat)中,单纯型法所得震源深度结果可靠性低,HypoSat方法所得结果较为可靠。因此,基于原震相,利用HypoSat方法重新定位,得到震源深度为9.7 km,与本研究结果基本一致。
4 结论综上所述,可以得到以下结论。
(1) 在YUS、XTT、JNX、LUQ地震台均识别出sPL震相,将理论波形与观测波形进行拟合,得到河北临城ML 4.4地震的震源深度在10—11 km,且sPL方法受地壳速度模型误差影响不大,速度增减10%,震源深度为10 km的地震测定结果偏差1 km(李志伟等,2015)。因此,如果认为文中使用的地壳速度模型与地下真实速度结构差异为10%,根据李志伟等(2015)的误差理论,则认为利用sPL震相测定的临城ML 4.4地震深度误差约1 km,与TMDT-INV方法(震源深度11—12 km)及PTD方法(震源深度11.6 km)的计算结果一致性较好,说明利用sPL震相计算所得震源深度可信度高。另外,崇加军等(2010)、Wang等(2011)、包丰等(2013)、项月文等(2014)、詹小艳等(2014)、李志伟等(2015)、彭利媚等(2017)研究发现,对于单个地震,一般只有1—2个地震台可以识别sPL震相。因此,对于此次临城ML 4.4地震,满足震中距条件的8个台站中虽仅有4个地震台sPL震相较明显,但结果基本一致,验证了此次震源深度测定结果的可靠性。
(2) 由公式(2)可知,当震中距大于
(3) 据崇加军等(2010)的研究成果,sPL震相一般出现在震中距50 km范围内,使用的4个台站中JNX台震中距(约60 km)稍大,可见,对于不同地区,sPL震相的优势震中距范围并不一致。
(4) sPL震相一般出现在较小震中距范围内,但在此范围内,并非每个台站均可观测到。该震相仅在构造相对简单区域发育,当SV波传播到节面附近时,则无法观测到该震相(Wang et al,2011)。河北临城地区东西部地质构造复杂,南北部构造变化小,而研究所用的4个台站分布在震中南北两侧,进一步说明该区东西部构造变化大,南北部差异较小,与实际地质情况相符。
5 讨论sPL震相属于近震深度震相,与P波到时差和震中距无关,仅与震源深度呈线性关系,且受地壳速度模型影响较小,为精确确定震源深度提供了较好的理论基础。另外,目前河北测震台网密度较大,一般较小震中距范围内宽频带台站较多,为寻找清晰的sPL震相提供了良好的数据基础。准确的震源深度有利于其他震源参数的确定,对于河北地区断层构造、活动性分析等具有较强的现实意义。
河北测震台网日常地震编目使用的4种定位方法中,单纯型属于搜索法,其余3种属于盖革法。地震定位方法对台站数量、分布、震相读取、地壳速度模型等要求较高,且在计算过程中,震源深度与发震时刻存在折衷,并非独立求解,尤其是浅源地震,当记录台站较少时,震源深度缺少可靠的约束条件,误差较大(中国地震局监测预报司,2017)。sPL震相方法利用P波与sPL震相到时差计算震源深度,与发震时刻无关,主要受地壳速度模型影响,且影响程度低,单台观测即可使用,观测台站越多,结果越可靠。后续研究发现,并非每个地震均能观测到sPL震相,所以该震相目前无法作为地震编目工作的常规手段,但可作为辅助验证手段,提高测震台网地震编目结果的可靠性。
感谢Dr. Lupei Zhu提供F—K计算理论地震图程序,感谢评审专家对本文提出的宝贵意见及建议。
| 包丰, 倪四道, 赵建和, 等. 时钟不准情形地震精确定位研究——以2011年1月19日安庆地震序列为例[J]. 地震学报, 2013, 35(2): 160-172. DOI:10.3969/j.issn.0253-3782.2013.02.003 | |
| 崇加军, 倪四道, 曾祥方. sPL, 一个近距离确定震源深度的震相[J]. 地球物理学报, 2010, 53(11): 2620-2630. | |
| 段刚.利用sPL震相测定福建仙游M4.6级地震震源深度[J/OL].地球物理学进展.[2018-12-22]. http://kns.cnki.net/kcms/detail/11.2982.p.20181022.1529.040.html. | |
| 河北省地质矿产局. 河北省北京市天津市区域地质志[M]. 北京: 地质出版社, 1989: 182-183. | |
| 李志伟, 黄志斌, 王晓欣, 等. USGS地震目录中4-5级震源深度异常地震可靠性初步研究:以南北地震带若干地震为例[J]. 地球物理学报, 2015, 58(4): 1236-1250. | |
| 林向东, 葛洪魁, 徐平, 等. 近场全波形反演:芦山7.0级地震及余震矩张量解[J]. 地球物理学报, 2013, 56(12): 4037-4047. DOI:10.6038/cjg20131209 | |
| 刘春, 吴忠良, 蒋长胜. 汶川地震序列中较大深度余震的一种可能的直接观测证据[J]. 中国地震, 2009, 25(2): 113-122. DOI:10.3969/j.issn.1001-4683.2009.02.001 | |
| 罗艳, 曾祥方, 倪四道. 震源深度测定方法研究进展[J]. 地球物理学进展, 2013, 28(5): 2309-2321. | |
| 彭利媚, 陈小敏, 王茺, 等. sPL震相在地震定位中的应用[J]. 高原地震, 2017, 29(2): 7-11. DOI:10.3969/j.issn.1005-586X.2017.02.002 | |
| 王莉婵, 朱元清, 李雪英, 等. 河北地区地壳一维速度模型的新近研究[J]. 华北地震科学, 2016, 34(4): 1-10. DOI:10.3969/j.issn.1003-1375.2016.04.001 | |
| 吴鹏, 李相平, 高原, 等. 邢台地区地壳各向异性特征初步研究[J]. 地震, 2017, 37(1): 73-81. | |
| 项月文, 罗丽, 肖孟仁, 等. sPL震相在九江-瑞昌MS 5.7地震序列震源深度测定中的应用[J]. 华北地震科学, 2014, 32(2): 7-13. DOI:10.3969/j.issn.1003-1375.2014.02.002 | |
| 杨选, 康英, 沈玉松, 等. 用爆破事件测试JOPENS-MSDP中4种定位算法的稳定性[J]. 地震地磁观测与研究, 2018, 39(4): 78-87. DOI:10.3969/j.issn.1003-3246.2018.04.010 | |
| 詹小艳, 朱升初, 王恒知, 薛莹莹, 王俊. sPL震相在江苏高邮M 4.9级地震震源深度测定中的应用[J]. 地球物理学进展, 2014, 29(4): 1609-1614. | |
| 张帆, 韩晓明, 郝美仙, 等. 2016年5月22日辽宁朝阳4.6级地震震源机制和震源深度研究[J]. 中国地震, 2017, 33(1): 141-153. DOI:10.3969/j.issn.1001-4683.2017.01.014 | |
| 郑勇, 谢祖军. 地震震源深度定位研究的现状与展望[J]. 地震研究, 2017, 40(2): 167-175. DOI:10.3969/j.issn.1000-0666.2017.02.001 | |
| 中国地震局监测预报司. 测震学原理与方法[M]. 北京: 地震出版社, 2017: 382-385. | |
| 朱元清, 石耀霖, 李平. 一种确定地震深度的新方法[J]. 地震地磁观测与研究, 1990, 21(2): 4-12. | |
| Aki K, Richards P. Quantitative seismology[M]. 2nd ed. Sausalito, CA: University Science Books, 2002. | |
| Greensfelder R W. The Pg-Pn method of determining depth of focus with applications to Nevada earthquakes[J]. Bull Seismol Soc Am, 1965, 55(2): 391-403. | |
| Wang Z J, Chong J J, Ni S D, et al. Determination of focal depth by two waveform based methods:A case study for the 2008 Panzhihua earthquake[J]. Earthquake Science, 2011, 24(4): 321-328. |
 2018, Vol. 39
2018, Vol. 39
