震级是表征地震强弱的相对量度。Richter (1935)根据美国加州的地震观测资料,提出利用短周期地震波资料确定的近震震级标度ML。在此基础上,Gutenberg (1945)提出面波震级标度MS,利用周期为20 s的面波振幅确定地震大小,还提出使用浅源地震P、PP和S波振幅确定的体波震级标度mb。ML、MS、mb震级是目前常用震级标度,使用范围不同,一般采用面波震级MS测定破坏性地震大小,采用近震震级ML测定中小地震大小。
对于同一个地震,根据不同震级标度测定的震级存在差异,不利于公众对地震的理解(陈运泰等,2004)。基于地震矩与面波震级的关系,Kanamori (1977)提出矩震级的概念,Hanks等(1979)给出矩震级定义式:MW = 2/3lgM0 -10.7,式中M0为地震矩,单位dyne·cm。矩震级的提出,较好解决了面波震级等已有震级标度存在的问题,该震级基于具有明确物理意义的地震矩,能反映地震破裂规模,且对于大震和小震均有定义,也不会产生震级饱和现象(陈培善等,1991)。
Kanamori (1977)根据能量与面波震级、能量与地震矩的关系,推导了地震矩与面波震级的关系式:lgM0 = 1.5MS +16.1。该关系式与Purcaru等(1978)根据实际资料给出的经验关系基本一致,但只适用于5.0—7.5级地震。Wells等(1994)的研究表明,在5.7<MS ≤8.0范围,面波震级MS与矩震级MW无系统偏差,对于5.7级以下或8.0级以上地震,面波震级MS略小于矩震级MW。Das等(2011)利用NEIC和GCMT的全球地震目录,计算面波震级到矩震级的转换公式。陈培善等(1989)使用1981—1983年全球约800个地震的面波震级和地震矩资料,按4个震级档分别给出地震矩与面波震级的关系,显示在6.4<MS ≤ 7.8范围,面波震级MS与矩震级MW基本一致。钟羽云等(2004)利用中国大陆1977—2001年发生的107次M ≥ 5.0地震资料,研究不同断层性质地震的地震矩与面波震级的关系。陈宏峰等(2014)利用2008年以来中国地震台网86个5.3级以上地震资料,统计矩震级MW与面波震级MS的经验关系。
考虑到我国地震台网测定的面波震级与国外存在一定差异(刘瑞丰等,2006),国外关于面波震级与矩震级关系的研究成果,在我国应用时需要论证其适用性。国内相关研究由于5级以下和6.5级以上地震样本较少,所得面波震级与矩震级关系的应用范围受到限制;另外,一些研究未给出统计关系的标准差,不利于量化计算结果的不确定性。
为建立适用于中国及邻区的面波震级与矩震级的统计关系,拟利用1990—2016年中国地震台网地震目录给定的面波震级和全球矩心矩张量(GCMT)项目提供的相应矩震级数据,使用分段加权最小二乘法,统计得到面波震级与矩震级的经验关系式,并给出相应标准差。
1 地震资料在研究中使用2类震级数据:面波震级和矩震级。其中,面波震级数据来自中国地震台网地震目录。该目录提供中国范围内地震震级数据,包括2种面波震级MS和MS7数据,分别采用SK中长周期地震仪和763型长周期地震仪的记录来确定震级大小。由于使用763型长周期地震仪记录确定的面波震级(MS7)与世界标准台网(WWSSN)的结果基本一致(刘瑞丰等,2006),而且我国763型长周期地震台网在20世纪80年代后期才建成并投入使用,故研究中使用1990—2016年的MS7震级数据。
因中国地震台网中心测定的地震矩震级与全球矩心矩张量(GCMT)项目发布结果基本一致(陈宏峰等,2014),故研究所用矩震级来自全球矩心矩张量(GCMT)项目数据。
从中国地震台网目录和GCMT矩震级目录中,挑选1990—2016年同时具有MS7震级和矩震级数据的地震,共得到860次MS7≥4.5浅源地震数据,其中:4.5—4.9级地震314次,5.0—5.9级地震419次,6.0—6.9级地震115次,7.0—7.9级地震10次,8.0—8.5级地震2次。
2 加权最小二乘法最小二乘法是一种数学优化技术,通过求解残差平方和的极值问题,寻找数据的最佳函数匹配,基本原理如下:设随机变量y与一组(k个)变量(x1,…,xk)服从关系式
| $ y = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + \ldots + {\beta _k}{x_k} + \varepsilon $ |
式中,(β0,β1,β2,…,βk)为未知参数,ε为随机项,服从正态分布N(0,σ2)。如果有n次测量结果(yi,xi1,xi2,…,xik),且i = 1,…,n,则
| $ {y_i} = \sum\limits_{j = 0}^k {{\beta _j}{x_{ij}} + {\varepsilon _i}} $ |
式中,(β0,β1,β2,…,βk)为未知参数;εi ≈ N(0,σ2)且E(εi,εj)= 0(i≠j;i,j=1,…,n),xi0 =1(i = 1,…,n)。
残差平方和Q为
| $ Q = \sum\limits_{i = 0}^n {{{\left[ {{y_i} - \left({{\beta _0} + {\beta _1}{x_{i1}} + \ldots + {\beta _k}{x_{ik}}} \right)} \right]}^2}} $ |
最小二乘法即寻找(β0,β1,β2,…,βk)的最优估计值,使得Q达到最小值。根据微积分的极值求法,可得到以下线性方程组
| $ \frac{{\partial Q}}{{\partial {\beta _0}}} = - 2\sum\limits_{i = 1}^n {\left[ {{y_i} - \left({{\beta _0} + {\beta _1}{x_{i1}} + \ldots + {\beta _k}{x_{ik}}} \right)} \right]} = 0 $ |
| $ \frac{{\partial Q}}{{\partial {\beta _1}}} = - 2\sum\limits_{i = 1}^n {\left[ {{y_i} - \left({{\beta _0} + {\beta _1}{x_{i1}} + \ldots + {\beta _k}{x_{ik}}} \right)} \right]} {x_{i1}} = 0 $ |
| $ \frac{{\partial Q}}{{\partial {\beta _k}}} = - 2\sum\limits_{i = 1}^n {\left[ {{y_i} - \left({{\beta _0} + {\beta _1}{x_{i1}} + \ldots + {\beta _k}{x_{ik}}} \right)} \right]} {x_{ik}} = 0 $ |
求解该线性方程组,即可得到(β0,β1,β2,…,βk)的最小二乘估计值,从而确定统计关系式。
本研究中小震级样本量远多于大地震,如果直接使用最小二乘法进行统计回归,则使统计关系式受控于小震级样本,以致在高震级处偏差较大。为解决此问题,拟采用按震级档进行加权的最小二乘法进行统计分析,使各震级档的样本对统计偏差的贡献率基本一致。
加权最小二乘法的思路:首先对原模型进行加权,使之成为一个新的不存在异方差性的模型,然后采用普通最小二乘法估计其参数。具体做法是考虑对残差平方和的贡献率,为每个样本赋予不同权重wi,则残差平方和Q由下式求得。
| $ Q = \sum\limits_{i = 0}^n {{w_i}} {\left[ {{y_i} - \left({{\beta _0} + {\beta _1}{x_{i1}} + \ldots + {\beta _k}{x_{ki}}} \right)} \right]^2} $ |
上式等同于统计样本为
考虑各震级档地震样本数量差别较大,拟按4.5—4.9级、5.0—5.9级、6.0—6.9级、7.0级以上4个地震分档进行加权,权重分别取1/314、1/419、1/115、1/12使每个分档样本对残差平方和贡献率一致,故各档权重取其样本量倒数。
3 统计结果及残差分析一般认为,矩震级与面波震级二者线性相关,符合以下关系式
| $ {M_{\rm{W}}} = a{M_{{\rm{S7}}}} + b $ |
式中,MW为矩震级,MS7为面波震级,a和b为待定参数。
采用上述线性关系式,使用按震级档加权的加权最小二乘法,对中国地震台网面波震级与矩震级数据进行回归分析,得到统计关系式、相应的均方差及相关系数如下
| $ {M_{\rm{W}}} = 0.805{M_{{\rm{S7}}}} + 1.154\;\;\;\;\sigma = 0.16\;\;\;\;r = 0.95 $ |
式中,σ为标准差,r为相关系数。
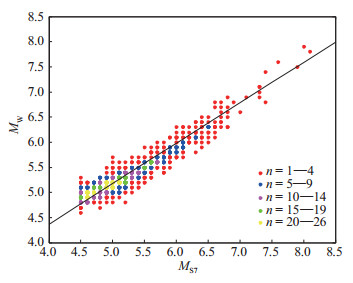
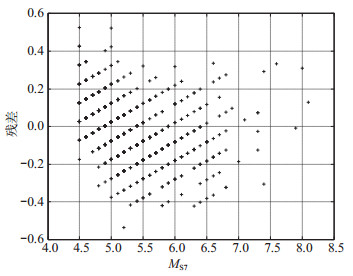
图 1显示所得到的统计关系和统计样本(图中圆点),图中以不同颜色代表样本点处的样本量n。整体而言,回归直线体现了矩震级与面波震级的线性关系,在5—7级范围内,统计样本点较均匀地分布在回归直线两侧,但回归直线稍偏离样本密集的中间带。尤其是对于5.0级以下和7.5级以上地震,统计样本主要分布在回归直线上方,表现出单侧偏离的特点,由统计残差(观测值减预测值)分布(图 2)可知,该现象更为明显,表明在所选地震震级范围(4.0—8.5级)内,线性关系不能完全体现矩震级与面波震级的相关性。
|
图 1 MW与MS7的线性关系和统计样本 Fig.1 Linear relationship between MW and MS7 and statistical samples |
|
图 2 线性回归的残差分布 Fig.2 The residuals distribution of linear regression |
为体现震级范围内矩震级与面波震级的关系,使用二次函数关系式作为新的统计关系式
| $ {M_{\rm{W}}} = aM_{{\rm{S7}}}^2 + b{M_{{\rm{S7}}}} + c $ |
式中,MW为矩震级,MS7为面波震级,a、b和c为待定参数。
采用该关系式,使用加权最小二乘法对数据进行回归分析,得到新的统计关系式、均方差及相关系数。
| $ {M_{\rm{W}}} = 0.082M_{{\rm{S7}}}^2 - 0.201M_{{\rm{S7}}}^{} + 4.145\;\;\;\;\sigma = 0.14\;\;\;\;r = 0.96 $ |
式中,σ为标准差,r为相关系数。
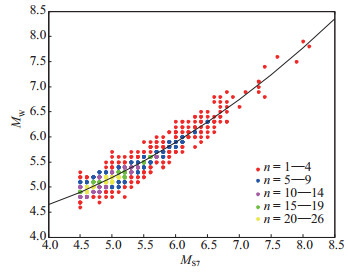
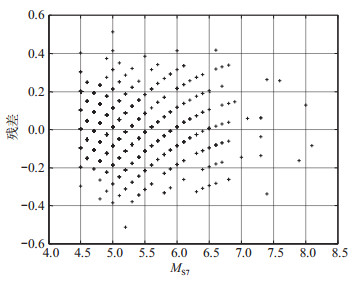
新的统计关系曲线(图中曲线)与统计样本(图中圆点)的拟合程度关系见图 3,图中以不同颜色代表该点处的样本量n,可以看出,统计曲线基本位于数据点密集的中线上,较好体现了统计样本的整体变化趋势。在震级统计范围内,样本基本均匀分布在统计曲线两侧。从残差分布(图 4)可知,残差基本均匀分布在0值线上下,说明在震级范围内统计关系式具有较好的无偏性。
|
图 3 MW与MS7的二次函数关系和统计样本 Fig.3 Quadratic relationship between MW and MS7 and statistical samples |
|
图 4 回归残差分布 Fig.4 The residuals distribution of regression |
本研究与陈培善等(1989)、Das等(2011)和陈宏峰等(2014)的统计关系对比见图 5。由图 5可见,陈培善等(1989)和Das等(2011)的统计关系较为一致,特别在MW 8.0以下,统计曲线主要位于该统计样本上界,相对偏高;陈宏峰等(2014)的统计关系直线靠近统计样本下界,因为使用基于SK地震仪记录的MS震级数据,该震级比MS7震级约高0.2级(刘瑞丰等,2006;翟璐媛等,2015)。本文给出的统计曲线基本位于样本分布密集中线上,表明样本数据与中国地震台网实际地震资料较为相符。

|
图 5 震级统计关系对比 Fig.5 Statistical relationships about magnitude |
综上所述,可以得到以下结论。
(1) 使用加权最小二乘法,给出中国地震台网面波震级MS7与矩震级的线性关系式和二次函数关系式,分析2种关系式的残差分布,认为二次函数关系式具有较好的无偏性,更能体现中国地震台网面波震级与矩震级的对应关系。
(2) 陈培善等(1989)和Das等(2011)的统计关系结果相近,很大程度上在于二者均使用全球地震资料,面波震级与MS7震级相近(刘瑞丰等,2006),所得统计关系曲线在震级为4.0—8.0时与本研究给出的曲线基本保持平行,震级整体约高0.2,可能反映了中国地震台网面波震级与矩震级关系的区域特征。
(3) 陈宏峰等(2014)的统计结果相对偏小,是因为使用基于SK中长周期地震仪记录的面波震级MS。考虑到该震级与MS7震级存在偏差(刘瑞丰等,2006;翟璐媛等,2015),认为其所得统计关系与本研究结果反映了同一内在规律。
(4) 在地震定量分析中,矩震级已逐渐取代面波震级等震级标度。对于中国及邻区4级以上地震,全球矩心矩张量(GCMT)项目发布的矩震级数据并不完整。对于此类无矩震级数据的地震,若测定MS7震级,可直接使用本研究给出的统计关系式,进行MS7震级到矩震级的转换;若仅测定MS震级,可参考翟璐媛等(2015)关于MS与MS7震级的统计关系式,将MS震级转换为MS7震级后,使用本研究关系式计算地震矩震级。
| 陈宏峰, 袁菲, 徐志国, 等. 使用中国地震台网资料快速测定中强地震矩震级[J]. 地震地磁观测与研究, 2014, 35(5/6): 51-57. | |
| 陈培善, 陈海通. 由二维破裂模式导出的地震定标律[J]. 地震学报, 1989, 11(4): 337-350. | |
| 陈培善, 白彤霞. 震源参数之间的定量关系[J]. 地震学报, 1991, 13(4): 401-411. | |
| 陈运泰, 刘瑞丰. 地震的震级[J]. 地震地磁观测与研究, 2004, 25(6): 1-12. DOI:10.3969/j.issn.1003-3246.2004.06.001 | |
| 刘瑞丰, 陈运泰, BormannP, 等. 中国地震台网与美国地震台网测定震级的对比(Ⅱ)——面波震级[J]. 地震学报, 2006, 28(1): 1-7. | |
| 翟璐媛, 张立文, 任克新, 等. 中国地震台网数字化后与美国地震台网面波震级对比分析[J]. 地震地磁观测与研究, 2015, 36(2): 19-25. DOI:10.3969/j.issn.1003-3246.2015.02.004 | |
| 钟羽云, 朱新运, 张震峰. 不同类型地震的地震矩-震级标度关系研究[J]. 西北地震学报, 2004, 26(1): 57-61. DOI:10.3969/j.issn.1000-0844.2004.01.010 | |
| Das R, Wason H R, Sharma M L. Global regression relations for conversion of surface wave and body wave magnitudes to moment magnitude[J]. Natural Hazards, 2011, 59(2): 801-810. DOI:10.1007/s11069-011-9796-6 | |
| Gutenberg B. Amplitudes of surface waves and magnitudes of shallow earthquakes[J]. Bull Seismol Soc Am, 1945, 35(1): 3-12. | |
| Gutenberg B. Amplitudes of P, PP, and S and magnitude of shallow earthquakes[J]. Bull Seismol Soc Am, 1945, 35(2): 57-69. | |
| Hanks T C, Kanamori H. A moment magnitude scale[J]. Journal of Geophysical Research:Solid Earth, 1979, 84(B5): 2348-2350. DOI:10.1029/JB084iB05p02348 | |
| Kanamori H. The energy release in great earthquakes[J]. Journal of Geophysical Research, 1977, 82(20): 2981-2987. DOI:10.1029/JB082i020p02981 | |
| Purcaru G, Berckhemer H. A magnitude scale for very large earthquakes[J]. Tectonophysics, 1978, 49(3/4): 189-198. | |
| Richter C F. An instrumental earthquake magnitude scale[J]. Bull Seismol Soc Am, 1935, 25(1/2): 1-32. | |
| Wells D L, Coppersmith K J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement[J]. Bull Seismol Soc Am, 1994, 84(4): 974-1002. |
 2018, Vol. 39
2018, Vol. 39
