2. 中国石家庄 050021 河北省环境地质勘查院;
3. 中国河北 063000 唐山市地震局
2. Hebei Survey Institute of Environmental Gelogy, Shijiazhuang 050021, China;
3. Tangshan earthquake Agency, Hebei Province 063000, China
地下水广泛存在于上地壳中,具有自由的流动性,对上地壳中发生的各种地壳动力作用响应灵敏。地下水动态受水文因素干扰的影响较大,对地震和构造活动具有较灵敏的响应(孙丽娟等,2004;孙小龙等,2013;付虹等,2014)。通过地下水异常现场落实与深入分析,力争判别并排除各种水文干扰,对地下水在地震前的异常变化作出肯定的确认,对提高地震分析预报能力,具有重要作用(车用太等,2004;车用太等,2011;孙小龙等,2013;盛艳蕊等,2015)。
地下水异常动态与干扰(影响)因素在成因上存在一定相关性,充分收集大气降水量和同层开采井的抽水量,采用消除趋势及年变化影响的数学处理方法,可提取地震趋势异常变化,判断其映震能力。马家沟矿井的水位动态主要受降雨量和地下水开采量影响,具有较为明显的年变形态,观测资料连续性较好,有一定映震能力,如:该井对1991年5月29日至30日唐山老震区MS 4.8、MS 5.2地震具有明显的映震反应(马希融,1995)。2010年马家沟矿井水位出现破年变异常,井水位加速持续上升,至2015年,最大上升幅度约30 m。这种大幅度水位上升异常变化,是否与区域地震构造活动有关,亦或水文因素干扰所致,本文通过调查分析马家沟矿井水位与降雨量、地下水开采的相关性,探讨水位大幅度上升的形成原因。
1 马家沟矿井地质环境马家沟矿井为静水位观测,井深920 m,含水段为地下736—920 m(图 1),奥陶系石灰岩岩溶裂隙水,水位动态属降雨补给—人工开采下降型,年变特征明显,具有雨季上升、旱季下降的特征,能记录到水震波。

|
图 1 马家沟矿井井孔柱状 Fig.1 The bar chart of well hole of Majiagou mine |
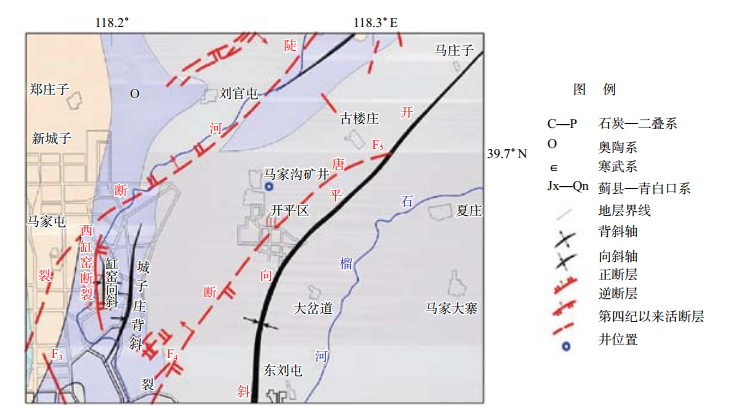
马家沟矿井位于开平向斜西北翼水文地质单元,周边地质构造复杂,发育一系列次级背斜、向斜和一些小规模断层(图 2),石灰岩地层破碎程度较大。本单元奥陶系地层上部为厚层豹皮状灰岩,中部为白云质灰岩,下部为竹叶状和带状灰岩,是唐山市区供水的主要基岩含水层和地下水开采层(尹宝军,2010;盛艳蕊等,2013)。从唐山奥陶系石灰岩含水层水文地质条件及该层地下水多年水位动态及开采状况分析,认为降雨补给和开采排泄是影响该层水位动态的2大主要因素(刘花台等,2002;宋利震等,2010)。
|
图 2 马家沟矿井周边地质构造 Fig.2 Geological structure of Majiagou mine |
2010年起马家沟矿井水位加速持续上升,收集矿井附近区域降雨量和地下地下水开采量资料,结合水位长期变化动态,分析水位上升的形成原因。
2.1 水位上升与降雨关系在唐山特定的水文地质条件下,奥陶系石灰岩地下水的补给是个复杂问题。在唐山北部,奥陶系石灰岩局部出露地表(在其他地区均被第四系覆盖),地下水可直接接受降水补给,在市区大城山一带还接受陡河水的补给(张素欣等,2002)。陡河两岸在大城山一带第四系较薄,个别地段奥陶系石灰岩裸露于河床,因处于城子庄背斜轴部,岩石破碎,为河水下渗提供渗透通道;又因拦河闸抬高陡河水位,使得静水压力加大,促进渗透。
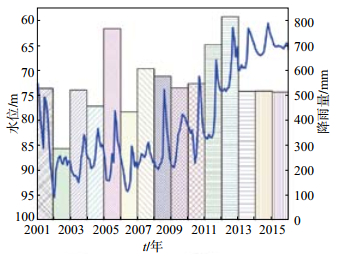
唐山市2001—2015年降雨量年平均值为556 mm,2001—2010年中有7年年降雨量在均值以下,陡河水量减少,河水对地下水的侧向补给也在减少。总之,水量补给在减少,水位出现大幅度上升(图 3,图中蓝色曲线表示矿井水位)。
|
图 3 马家沟矿井水位与区域降雨量对比 Fig.3 The comparison of the rainfall of the Majiagou mine and the region |
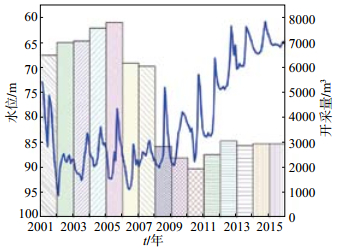
马家沟矿井水位与周边地下水开采量对比见图 4(图中蓝色曲线表示矿井水位),可见水位动态变化与矿井周边地下水开采量存在一定相关性。由图 4可见,由于长期开采地下水,地下水位多年呈下降趋势,2008—2009年缓慢回升,2010年后上升速率突然增大,截至2015年水位变幅约30 m,目前已基本稳定,回升幅度有所减小。马丙太等(2016)的研究表明,自2008年以来唐山市水务局关停企业自备井,浅层水和地下水水位同步上升,且上升幅度较大,对地下水位观测产生较大干扰。由此可见,马家沟矿井水位的上升异常可能与周边地下水开采活动有关。
|
图 4 马家沟矿井水位与周边地下水开采量对比 Fig.4 Comparison of mine and surrounding groundwater exploitation in Majiagou mine |
唐山奥陶系石灰岩含水层的富水性和导水性,受岩溶、裂隙发育程度及分布规律控制,表现出强烈的不均一性,使得岩溶裂隙水的流动状态较为复杂。在此条件下,采用现有地下水动力学方法计算,所需各项水文地质参数及边界条件难以确定,进行水位动态和降雨量、开采量关系的计算则产生较大困难。为此,采用回归分析模型与三维地下水流动模型,分析2001—2015年马家沟矿井水位上升的原因。
3.1 回归分析模型回归分析模型适用于水文地质条件复杂,且长期进行地下水位观测的地区(张建芝等,2010;张海飞,2016)。该模型中显著性水平的数值为结果可信程度的一个递减指标,值越大,越不能认为样本中变量的关联是总体中各变量关联的可靠指标,如数值为0.05,提示样本中变量关联有5%的可能是由偶然性造成的。通过F检验可以说明线性关系显著,一般线性相关系数在0.7以上,则表明变量和自变量之间存在线性关系。
统计唐山市2001—2015年的年平均地下水位、市区开采量、降雨量、前1年市区开采量和市区前2年的地下水开采量及降雨量,分别建立地下水开采量及降雨量的多元回归模型,分析影响地下水位变化的主要因素。
(1)地下水开采量多元回归模型。考虑到地下水开采对井水位的即时及滞后效应,建立多元回归模型(汪成民等,1988)。
| $ Y={{\beta }_{0}}+{{\beta }_{1}}{{X}_{1}}\text{+}{{\beta }_{2}}{{X}_{2}}\text{+}{{\beta }_{3}}{{X}_{3}}\text{+}{{\beta }_{4}}{{X}_{4}}\text{+}\varepsilon $ | (1) |
其中:Y为年平均地下水位,X1为当年降雨量,X2为当年开采量,X3为前1年开采量,X4为前2年开采量,β0、β1、β2、β3、β4为回归系数,利用数理统计软件对数据进行处理,得到回归方程,则
| $ Y=20.651+0.011{{X}_{1}}-0.001{{X}_{2}}-0.004{{X}_{3}}+0.005{{X}_{4}} $ | (2) |
设定该模型的显著性水平为0.05,对式(2)进行F统计检验,则
| $ F=12>{{F}_{0.05}}\left(4, 8 \right)=3.84 $ | (3) |
相关系数为0.746,大于0.7,说明式(2)的线性关系显著。说明自变量与因变量之间的线性关系显著,模型精度较高,预测结果可靠。
在地下水开采量多元回归模型显著水平为0.05时,对自变量参数进行检验,结果表明,前1年的开采量和前2年的开采量对地下水位有显著影响,而降雨量、当年市区开采量对地下水位无显著影响。
(2)降雨量多元回归模型。考虑到降雨对井水位的即时及滞后效应,建立多元回归模型,见式(1),此时,式中:Y为年平均地下水位,X1为当年降雨量,X2为当年开采量,X3为前一年降雨量,X4为前两年降雨量,β0、β1、β2、β3、β4为回归系数。同理,得到回归方程,则
| $ Y=59.354-0.012{{X}_{1}}+0.003{{X}_{2}}\text{+0}\text{.008}{{X}_{\text{3}}}\text{-}0.017{{X}_{4}} $ | (4) |
同理,设定回归模型显著性水平为0.05,对式(4)进行F统计检验,则
| $ F=2 < {{F}_{0.05}}\left(4, 8 \right)=3.84 $ | (5) |
相关系数为0.479,小于0.7,说明式(4)的线性关系不显著。说明自变量与因变量之间的线性关系不显著, 模型精度较低, 预测结果不可靠。
综上可知,通过多元回归分析,马家沟矿井地下水开采量多元回归模型线性关系显著,而降雨量模型线性关系不显著,表明2001—2015年马家沟矿井地下水位上升主要由地下水开采量减少所致。
3.2 三维地下水流动模型为了建立合理的三维地下水流动模型,将模拟区域扩大至开平向斜西北翼。该区域地质构造复杂,上覆第四系,厚度随下伏基岩顶面起伏变化较大(20—180 m),第四系孔隙含水组与奥陶系灰岩含水组水力联系密切。马家沟矿井观测层位为奥陶系含水层,依据该区域地层分布资料建立三维空间模型,其中空间范围长14 000 m,宽15 000 m,厚200 m。
对于各向异性多孔介质,设坐标轴方向与各向异性介质主方向一致,则承压水非稳定运动的基本微分方程(薛禹群等,1997)可以表示为
| $ \left\{ \begin{align} & \frac{\partial }{\partial x}\left({{K}_{xx}}\frac{\partial H}{\partial x} \right)+\frac{\partial }{\partial y}\left({{K}_{yy}}\frac{\partial H}{\partial y} \right)+\frac{\partial }{\partial z}\left({{K}_{zz}}\frac{\partial H}{\partial z} \right)+W={{\mu }_{s}}\frac{\partial H}{\partial t} \\ & H\left(x, y, z, t \right)\left| _{t=0}={{H}_{0}}\left(x, y, z \right) \right. \\ & K\frac{\partial H}{\partial n}\left| _{{{r}_{2}}}=0 \right. \\ \end{align} \right. $ | (6) |
式中:H为水头;t表示时间;Kxx、Kyy、Kzz分别表示含水层在x、y、z轴方向上的渗透系数;n为含水层贮水率;W为单位体积流量,用以表示从单位体积含水层中流入(为正)或流出(为负)的水量,假设渗透系数K和贮水率不受含水层孔隙度变化(骨架变形)的影响。
式(6)加上相应的初始条件和边界条件,便可构成描述地下水流动体系的数学模型,文中采用有限差分法(向后差分法)来求解。模型中水平方向边界条件根据区域构造设定,其中北、东、西方向分别为陡河断裂、唐山断裂,均为隔水断裂,设定为隔水边界,南侧为水头边界;垂直方向上,第四系含水层接受大气降水补给,第四系、奥陶系基底均为隔水层。查阅相关资料得知,研究区奥陶系平均渗透系数K约为152 m/d。在计算过程中,设奥陶系含水层总的等效厚度为180 m,其垂向渗透系数为水平方向渗透系数的1/10。
基于以上三维地下水流动模型,赋予相应水文参数,计算开平向斜西北翼地区降雨量、地下水开采量对区域水位的影响程度。设:2001年1月1日至2015年12月31日为模拟校核期,2016年1月1日至2020年12月31日为模型预测期,该期降雨量采用2015年数据,地下水开采量采用2005年数据(统计时段内抽水量最大),绘制马家沟矿井水位实测值与模拟值对比曲线,见图 5。由图 5可见,2016年1月1日起地下水开采量增大,水位逐年下降,表明马家沟矿井地下水水位动态异常变化主要受地下水开采量影响。

|
图 5 马家沟矿井实测值与模拟值对比曲线 Fig.5 Comparison curve between the measured value and simulated value of Majiagou mine |
综上所述,可以得到以下结论。
(1)马家沟矿井水位多年趋势上升,主要由区域地下水开采量减少引起。由地下水开采量和地下水位上升幅度的相关性特征可知,2008年以前,地下水开采活动较多,开采量较大,马家沟矿井地下水位多年呈下降趋势;2008年以后,唐山市水务局关停工矿企业自备井,地下水开采量逐渐减少,直接导致该区域地下水水位的快速上升。
(2)多元线性回归模型和三维地下水流动模型适用于水文地质条件复杂,且长期开展地下水位观测的地区。通过模型分析可知,在开平向斜西北翼水文地质单元内,人工地下水开采量对地下水水位多年动态变化规律起主要作用,该结论可为以后马家沟矿井地下水动态异常识别及判定提供一定借鉴意义。
(3)地下水位异常动态变化与干扰(影响)因素存在一定相关性,详细统计大气降水量和同层开采井的抽水量,采用消除趋势及年变化影响的数学处理方法,可提取地震发生前后地下水位趋势异常变化,判断其映震能力。马家沟矿井水位自观测以来资料连续性较好,近年受地下水开采不稳定的影响,年变动态出现异常变化,在今后资料分析中应充分考虑水文环境干扰对井水位观测的影响。
马家沟矿井水位动态观测层与地下水开采层为同一含水层,地下水开采量的变化引起井水位出现年变规律改变或短期破年变异常,对于其他类似井孔,若地下水位观测出现同样的异常变化,可首先分析地下水开采对观测数据的影响,再考虑其他因素。
| 车用太, 鱼金子, 黄振义, 等. 唐山大震地下水位前兆场的特征及其形成与演化模式[J]. 地震, 1994(Z1): 33-39. | |
| 车用太, 鱼金子, 刘成龙, 等. 判别地下水异常的干扰性与前兆性的原则及其应用实例[J]. 地震学报, 2011, 33(6): 800-808. DOI:10.3969/j.issn.0253-3782.2011.06.010 | |
| 车用太, 鱼金子. 地下流体典型异常的调查与研究[M]. 北京: 气象出版社, 2004. | |
| 付虹, 邬成栋, 赵小艳, 等. 云南开远井水位异常分析[J]. 地震学报, 2014, 36(2): 292-298. | |
| 刘花台, 王贵玲, 刘志明, 等. 唐山中西部地区地下水位动态特征分析[J]. 勘察科学技术, 2002(6): 16-20. DOI:10.3969/j.issn.1001-3946.2002.06.004 | |
| 马丙太, 庞国兴. 唐山北郊水源地地下水多年动态变化分析[J]. 地下水, 2016, 38(2): 84-85. DOI:10.3969/j.issn.1004-1184.2016.02.030 | |
| 马希融. 一次可靠的地下水位临震异常[J]. 华北地震科学, 1995, 13(3): 70-80. | |
| 盛艳蕊, 张子广, 张素欣, 等. 昌黎井水位破年变异常分析[J]. 中国地震, 2015, 31(2): 399-408. DOI:10.3969/j.issn.1001-4683.2015.02.025 | |
| 盛艳蕊, 张子广, 张素欣, 等. 楼盘施工注浆及荷载对唐山矿井水位的影响分析[J]. 中国地震, 2013, 29(1): 142-147. DOI:10.3969/j.issn.1001-4683.2013.01.016 | |
| 宋利震, 庞国兴, 马丙太, 等. 唐山西郊地区地下水多年动态变化分析[J]. 地下水, 2010, 32(6): 106-107. DOI:10.3969/j.issn.1004-1184.2010.06.039 | |
| 孙丽娟, 冀林旺, 金镇洪, 等. 山龙峪井水位异常与地震关系初探[J]. 东北地震研究, 2004, 20(1): 42-47. DOI:10.3969/j.issn.1674-8565.2004.01.007 | |
| 孙小龙, 刘耀炜, 马玉川. 鲁豫交界地区深井水位持续大幅度下降原因分析[J]. 中国地震, 2013, 29(1): 132-141. DOI:10.3969/j.issn.1001-4683.2013.01.015 | |
| 孙小龙, 刘耀炜, 晏锐. 云南姚安井2009年10月后水位下降的成因分析[J]. 地震学报, 2013, 35(3): 410-420. DOI:10.3969/j.issn.0253-3782.2013.03.012 | |
| 汪成民, 车用太, 万迪堃, 等. 地下水微动态研究[M]. 北京: 地震出版社, 1988. | |
| 薛禹群, 朱学愚, 吴吉春, 等. 地下水动力学[M]. 北京: 地质出版社, 1997. | |
| 尹宝军, 马丽, 陈会忠, 等. 汶川8.0级地震及其强余震引起的唐山井水位同震响应特征分析[J]. 地震学报, 2009, 31(2): 195-204. DOI:10.3321/j.issn:0253-3782.2009.02.009 | |
| 尹宝军.唐山井地下水动态特征研究[D].北京: 中国地震局地球物理研究所, 2010: 28-34. http://www.cnki.com.cn/Article/CJFDTotal-GJZT201103012.htm | |
| 张海飞. 地下水动态预测模型概述[J]. 地下水, 2016, 38(1): 68-70. DOI:10.3969/j.issn.1004-1184.2016.01.023 | |
| 张建芝, 邢立亭. 回归分析法在地下水动态分析中的应用[J]. 地下水, 2010, 32(4): 88-90. DOI:10.3969/j.issn.1004-1184.2010.04.035 | |
| 张素欣, 温学勤, 郑云贞, 等. 地下水动态多年周期与中强震多发期[J]. 华北地震科学, 2002, 20(1): 32-37. DOI:10.3969/j.issn.1003-1375.2002.01.005 |
 2018, Vol. 39
2018, Vol. 39

