地震波传播过程中能量衰减是地震研究的重要课题,对于地震波传播过程中的非弹性衰减,地震学上用品质因子Q值来加以度量。Q值是地球介质的一个重要基本参数,也是地震定量分析及震源性质研究所必须的重要参数,在震源物理、工程地震研究、地震预测预报等领域具有重要的应用价值,也是地震学研究的重要组成部分。Q值的物理含义表明,Q值大小与介质的均匀程度相关,与区域构造活动有较大相关性。介质的均匀程度低,则地震波经过时能量损耗大,衰减较快,Q值较低。一般,构造活动较为活跃、频繁的地区,介质的均匀程度相对较低,Q值较低。因此,求解区域品质因子Q值,可在一定程度上探明地下介质的非均匀性程度与非弹性特征,了解介质地震构造活动情况。
五大连池火山区位于黑龙江省西北部,整个火山区域内发育火山锥14座。张凤鸣(1996)等通过地震监测工作发现,五大连池火山区内火山构造地震活动较为频繁,表明火山构造活动仍在持续。尤其以距今喷发280年的老黑山、火烧山NE向断裂为地震密集带2011年五大连池火山区发生一次ML 4.2地震,震中(48.6°N,126.0°E),恰好位于老黑山、火烧山NE向断裂带附近。以往对该区域火山构造地震活动与火山地质关系的研究表明,火山构造地震空间分布受火山构造活动控制,在国内外火山区域地震构造活动性评估研究(梁国经等,2011)中,区域品质因子Q值是一个较好的指标和判据。本文利用五大连池火山区域火山测震台站地方震资料,运用Atkinson等(1992)给出的三段衰减模型,采用最小二乘反演方法,分别计算求取火山区及老黑山、火烧山附近区域S波和体波的Q值与频率f的关系,分析该区域体波Q值特征。
1 数据资料五大连池火山测震台网历经多次改造和维护,目前有4个子台在运行。由于各种原因,近年来测震台网子台运行断断续续,仅北山子台运行稳定,无长时间断记,资料连续性较好,其他子台有些甚至中断较长时间,数据资料不完整。
北山子台位于海拔高度310 m的高地,周围观测环境清新,干扰少,台基为燕山期花岗岩,经“十五”数字化地震台网改造,自2001年开展数字化地震监测以来,数据连续率较高,积累大量五大连池火山区地震波形记录,震中空间分布涵盖五大连池火山区域,为本研究垫定了良好的数据基础。北山子台基本信息及仪器配备见表 1。
| 表 1 五大连池北山地震台基本信息 Tab.1 The basic information of Wudalianchi Beishan Seismic Station |
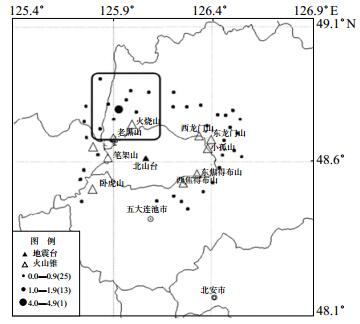
为保证地震多台定位准确及参与反演的震源距离数据较为准确,地震挑选原则如下:直达P波、S波清晰,信噪比较高,振幅不饱和,干扰小,地震数据同时由测震台网其他子台接收。为此,收集2008—2016年五大连池火山区典型中小火山地震,得到符合条件的39个地震,其中ML 0.0—0.9地震25次,ML 1.0—1.9地震13次,ML 4.0—4.9地震1次,主要分布于2条NE向断裂带及周围区域,最大震中距不超过300 km。所选地震序列、测震台网子台、火山锥分布见图 1,可见地震震中较好分布在火山区域,其中黑色方框部分为地震密集区域,即在清朝发生火山喷发的老黑山、火烧山的NE向断裂区域。
|
图 1 地震台、火山锥、地震震中分布 Fig.1 Distribution of earthquake station, volcano cone and seismic epicenter |
地震仪记录的地震波是一种综合信息,包含地震的震源效应、地震波传播路径效应、台站场地响应、仪器响应和噪声。在时间域里,地震记录位移可用以下公式解释。
| $ {A_{ij}}\left(t \right) = {S_i}\left(t \right) \otimes {P_{ij}}\left(t \right) \otimes {L_j}\left(t \right) \otimes {I_j}\left(t \right) \otimes {N_j}\left(t \right) $ | (1) |
其中,Aij(t)为第i个地震在第j个台站记录的地震记录位移(速度计或加速度型地震仪记录,可以通过积分得到位移记录),Si(t)为震源效应,Pij(t)为传播路径效应,Lj(t)为台站场地响应,Ij(t)为仪器响应,Nj(t)为台站噪声。将式(1)在频率域进行转换,上述卷积形式转换为乘积形式
| $ {A_{ij}}\left(f \right) = {S_i}\left(f \right) \cdot {P_{ij}}\left(f \right) \cdot {L_j}\left(f \right) \cdot {I_j}\left(f \right) \cdot {N_j}\left(f \right) $ | (2) |
式中,Pij(f )为与品质因子Q值相关的传播路径衰减项,则
| $ {P_{ij}}\left(f \right) = G\left({{R_{ij}}} \right) \cdot {e^{\frac{{{\rm{ \mathsf{ π} }}{R_{ij}}f}}{{Q\left(f \right)v}}}} $ | (3) |
式中,G(Rij)为地震波在传播过程中的几何衰减项,Q(f)为介质品质因子值,Rij为地震震源距,v为地震波速度。去掉仪器响应Ij(f )(利用每年标定数据予以剔除)和台站噪声Nj(f ),并将几何衰减项G(Rij)和非弹性衰减项代入式(1),则
| $ {A_{ij}}\left(f \right) = {S_i}\left(f \right) \cdot G\left({{R_{ij}}} \right) \cdot {e^{\frac{{{\rm{ \mathsf{ π} }}{R_{ij}}f}}{{Q\left(f \right)v}}}} \cdot {L_j}\left(f \right) $ | (4) |
对于式(4)中的几何衰减项G(Rij),地震学家和地震工程学家做了大量研究,总结大量理论和实际观测结果,得到以下经验公式,即已知某地区地壳厚度,参照Atkinson等(1992)的研究,采用互相衔接的三段几何衰减函数,对于体波,可得
| $ G({R_{ij}}) = \left\{ {\begin{array}{*{20}{l}} {R_{ij}^{ - {b_1}}}&{\left({{R_{ij}} \le {R_1}} \right)}\\ {R_1^{ - {b_1}}R_1^{{b_2}}R_{ij}^{ - {b_2}}}&{\left({{R_1} \le {R_{ij}} \le {R_2}} \right)}\\ {R_1^{ - {b_1}}R_1^{{b_2}}R_2^{ - {b_2}}R_2^{{b_3}}R_{ij}^{ - {b_3}}}&{\left({{R_{ij}} \ge {R_2}} \right)} \end{array}} \right. $ | (5) |
式中:b1=1、b2=0.019、b3=0.5、R1=1.5H、R2=2.5H(H为区域地壳厚度)。由式(5)可知,当Rij≤R1时,对应直达波几何衰减;当R1≤Rij≤R2时,对应过渡区,在该震源距范围内,直达波中加入地壳内间隔面和莫霍面上的过临界反射波;当Rij≥R2时,对应多次折射反射S波的衰减。在三段几何衰减模型中,其衰减指数b1、b2、b3均被认为与频率无关。将三段几何衰减模型代入,等式两边取对数,可得
| $ \begin{array}{l} \log {A_{ij}} = \log {S_i}\left(f \right) - {b_1}\log {R_{ij}} + \frac{{{\rm{ \mathsf{ π} }}{R_{ij}}f}}{{Q\left(f \right)v}}\\ \log e + \log {L_i}\left(f \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({R_{ij}} \le {R_1}) \end{array} $ |
| $ \begin{array}{l} \log {A_{ij}} = \log {S_i}\left(f \right) - {b_1}\log {R_{01}} - {b_2}\log\left({{R_{ij}}/{R_{01}}} \right)\\ \frac{{{\rm{ \mathsf{ π} }}{R_{ij}}f}}{{Q\left(f \right)v}}\log e + \log {L_i}\left(f \right)\;\;\;\;\;\;\;\;\;\;\;\;\;({R_1} \le {R_{ij}} \le {R_2}) \end{array} $ |
| $ \begin{array}{l} \log {A_{ij}} = \log {S_i}\left(f \right) - {b_1}\log {R_{01}} - {b_2}\log\left({{R_{02}}/{R_{01}}} \right) - {b_3}\\ \log\left({{R_{ij}}/{R_{02}}} \right)\frac{{{\rm{ \mathsf{ π} }}{R_{ij}}f}}{{Q\left(f \right)v}}\log e + \log {L_i}\left(f \right)\;\;\;\;\;({R_{ij}} \ge {R_2}) \end{array} $ |
对于以上几个公式,未知量仅震源谱部分logSi(f)、非弹性衰减项
根据三段几何衰减模型及最小二乘反演计算原理,编制对应的计算软件求取Q值,主要运算过程有以下几个步骤。
(1) 根据原始事件波形Pg波与Sg波到时差估算震源距。
(2) 采用平移窗谱方法,将波形数据由时间域转换至频率域,获得稳定的波形数据傅里叶谱。具体方法是:将S窗内的波形分成若干包含256个采样点的小段,并使相邻小段之间有50%的重叠。对于采样率为50 Hz的地震记录,每个小段的时间长度为5.1 s。在每一小段波形的起始和末尾加5%的COS边瓣,通过快速傅里叶变换,得到各小段傅里叶谱,进行仪器响应校正,计算得到S窗内观测信号的位移谱振幅,公式如下
| $ u\left(f \right) = \left\{ {\left[ {\sum\limits_{i = 1}^n {v_i^2} \left(f \right)} \right] \cdot T/{{\left({n \cdot t} \right)}^{\frac{1}{2}}}} \right\}/\left({2{\rm{ \mathsf{ π} }}f} \right) $ |
式中,vi2(f )为S波第i小段傅里叶快速变换谱(波形记录经仪器响应校正及分割),T为S窗(包含n个时间长度为t的256个采样点的小段)的持续时间。通过内插得到27个频率点(对数频率为0.0,0.05,0.1,0.15,0.2,…,1.3)的加速度谱振幅值。
(3) 剔除地震记录频率域背景噪声。对于选取信噪比大于2的地震记录,采集其地震记录P波初至之前256个采样点的噪声记录,计算其噪声位移谱振幅N(f),后在原记录谱中予以剔除。N(f)计算公式为
| $ N\left(f \right) = \left\{ {v_{\rm{N}}^2\left(f \right) \cdot T/{t^{\frac{1}{2}}}} \right\}/\left({2{\rm{ \mathsf{ π} }}f} \right) $ |
其中,N(f )为位移谱,vN(f )为经仪器校正的噪声速度谱。
(4) 在频率域,利用最小二乘反演,计算上述地震波谱在不同频率点f下的
对于选取的39个火山地震的原始波形记录,截取S波,得到去除背景噪声、仪器响应项后的地震位移振幅谱,采用最小二乘法,对于不同的频率点f分别进行反演,得到对应的f与Q(f )的关系。在此以五大连池火山区北山台记录的10个地震原始波形为计算实例,给出地震原始波形及位移振幅谱,见图 2,图 2(b)中红色线条为内插频点后的位移频率谱。

|
图 2 10个地震S波段位移振幅谱 (a)原始波形;(b)位移幅谱 Fig.2 The displacement amplitude spectrum of S wave |
采取上述计算过程处理全部地震资料,得到该区域品质因子Q值,采用双对数坐标系,绘制f与Q(f)的关系图,见图 3。由图 3可见,logQ(f)与logf表现出较好的线性关系,且f ≥ 100时,部分线性关系较为准确。采用f ≥ 100的频率结果进行拟合,得到五大连池火山地区f与Q(f)的依赖关系,即:Q(f) = 221.7f 0.452。

|
图 3 品质因子Q(f)与频率f的关系 Fig.3 The relation between quantity factor Q(f) and frequency f |
采用三段几何衰减模型,国内外诸多学者对不同区域进行研究,得到相应体波Q值,如:Atkinson等(1992)对加拿大东南部和北美东部地震波衰减特征进行研究,分别得到Q(f)=670.0f 0.330、Q(f)=680.0f 0.360;Malagnini等(2000)反演得到意大利亚平宁半岛地区地震波f与Q(f)的关系:Q(f)=130.0f 0.100;刘杰(2003)反演得到成都及广东地区地震波f与Q(f)的关系,分别为:Q(f)=203f 0.834,Q(f)=454.8f 0.37;郭晓(2008)反演得到青藏高原地区地震波f与Q(f)的关系:Q(f)=564.7f 0.3;邬成栋(2013)反演得到云南小湾水库附近地震波f与Q(f)的关系:Q(f)=225.8f 0.332。在本研究中,笔者将震中位于老黑山、火烧山区域的地震进行反演,计算得到f与Q(f)的关系:Q(f) = 152f 0.600。
4.2 Q值特征在体波Q值频率拟合关系式Q(f) = Q0 f η中,Q0的大小与介质的非均匀程度相关联,反映震源到地震台站射线周围介质的平均性质。介质的非均匀程度高,地震波通过时能量损耗大,衰减快,Q0值较低。介质非均匀程度低,情况则相反。一般,构造活动较稳定的地区介质的非均匀程度较低,构造活动强烈的地区介质的非均匀程度相对较高。与之相应,前者的Q0值较高,后者的Q0值较低。而η值则相反,介质均匀程度较低的地区,Q与频率f的依赖关系较强,η值可能较大;介质均匀化程度较高地区,Q值与频率f的依赖关系较弱,η值可能较小。
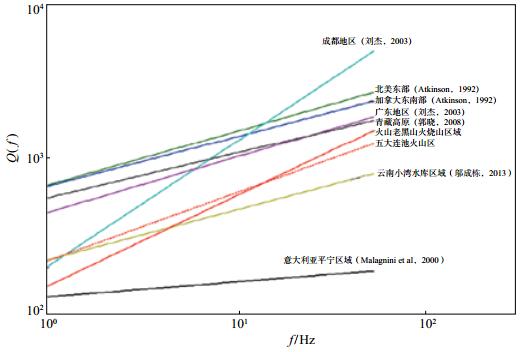
将以上国内外区域体波Q值与f的关系进行对比,绘制图 4,图中红点线为五大连池火山区,红线为老黑山、火烧山活动火山区域。由图 4可见,文中五大连池区域及其火山群中NW向老黑山、火烧山区域Q0水平均较低。由以上地震波f与Q(f)的关系式可知,成都地区和云南小湾水库区域Q0值均较低(与五大连池及其活动火山区域Q0值处于同一水平),均为地震构造活动较为频繁的多震地区。因此,五大连池火山地区的地质构造活动活跃,与本区域地震活动水平较频繁(张凤鸣等,1996)一致。
|
图 4 国内外Q值结果对比 Fig.4 The comparison of Q value between the alien and the domestic |
老黑山与火烧山这对新期火山群,曾于1720年1月至3月持续喷发,由图 4可见,其Q0值比五大连池火山区平均水平低,同时η值比平均水平高,Q值与频率f的依赖关系较强,与成都地区处于同一水平,部分地震学者,如Aki(1980)认为,在火山地区Q与频率f的依赖关系较弱,为弱相关性,该现象形成的原因是大量岩浆存在的结果。本研究测得老黑山与火烧山的Q与频率f表现出较高的相关性,根据赵谊等(1999)、彭年等(2005)对五大连池新期火山岩浆房的研究,认为老黑山与火烧山岩浆房近乎固结,而本研究中二者Q值与频率f表现出较高的相关性,从侧面排除五大连池火山存在大量岩浆的可能性,并且笔者(高亮等,2013)在对该区域的尾波Q值研究中尾波Q值也表现出相同的特征。
5 结论在区域地震活动性研究中,研究区域介质地震波的非弹性衰减特征品质因子Q是一个重要方面,本研究根据五大连池火山区域小范围近震资料,计算得到该区品质因子值Q(f) = 221.7f 0.452,其新期火山老黑山、火烧山区域品质因子值为Q(f) = 152f 0.600,结合国内外其他资料对比可知,本区域体波Q值较其他地区低,符合构造活动剧烈的介质特征,而且老黑山、火烧山区域品质因子Q0更低,且与频率f表现出较强的相关性,从侧面排除五大连池火山群存在大量岩浆的可能性,进一步佐证了赵谊等(1999)、彭年等(2005)对老黑山与火烧山火山岩浆房近乎固结的结论。
| 高亮, 张守国, 闫峰. 五大连池火山区尾波Q值研究[J]. 地震地磁观测与研究, 2013, 34(1/2): 41-46. | |
| 梁国经, 李仲巍, 郑双凤, 等. 龙岗火山区尾波Q值的初步研究[J]. 地震地质, 2011, 33(1): 114-122. DOI:10.3969/j.issn.0253-4967.2011.01.011 | |
| 彭年, 刘永顺, 韦玉凤. 五大连池新期火山岩浆房动力稳定性探讨[J]. 岩石矿物学杂志, 2005, 24(3): 198-204. | |
| 张凤鸣, 张守国, 邹卫东. 五大连池火山构造地震空间分布及其构造含义[J]. 东北地震研究, 1996, 12(4): 17-22. | |
| 赵谊, 邹卫东, 周皓. 五大连池火山危险性分析[J]. 自然灾害学报, 1999, 8(4): 140-146. | |
| Aki K. Attenuation of shear-waves in the lithosphere for frequencies from 0.05 to 25 Hz[J]. Physics of the Earth and Planetary Interiors, 1980, 21(1): 56-60. | |
| Aki K. Scattering and attenuation of shear waves in the lithosphere[J]. Journal of Geophysical Research:Solid Earth, 1980, 85(B11): 6496-6504. DOI:10.1029/JB085iB11p06496 | |
| Atkinson G M, Mereu R F. The shape of ground motion attenuation curves in southeastern Canada[J]. Bull Seismol Soc Am, 1992, 82(5): 2014-2031. |
 2018, Vol. 39
2018, Vol. 39
