2. 中国北京 100081 中国地震局地球物理研究所
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
震级是表示地震大小的量,是地震基本参数之一。自从1935年里克特提出地方性震级标度ML以来,震级得到各个国家的普遍使用。ML是一个没有量纲的地震参数,测定和使用比较方便,更重要的是,它为面波震级MS、体波震级mb和mB以及宽频带体波震级mB(BB)、宽频带面波震级ΜS(BB)的建立提供了思路与方法。
震级不是一个物理量,震级标度是经验性的,与地震发生的物理过程无直接联系,物理意义也不清楚。最突出的例证是,在震级定义中连量纲都不对,在地方性震级、面波震级和体波震级的计算公式中,均通过对位移的振幅A或A与周期T的比值取对数求得。众所周知,只能对无量纲的量求对数(陈运泰等,2004)。
对于构造地震来讲,岩层在大地构造应力的作用下产生应变,并不断积累应变能,应力一旦超过极限,岩石就会突然破裂,或沿原破裂面滑动,释放出大量能量,这就是地震成因的断层假说。地震发生时释放出来的能量,大部分以机械能(岩石破裂和位移)和转换为热能的形式存在震源区,一部分以地震波的形式向四面八方传播。地震时以地震波形式传播的能量称为地震波辐射能量,简称地震辐射能,或地震波能量。地震波能量是地震释放总能量的一部分,而正是这部分能量对地震波传播所经过区域造成了破坏。因此,从减轻地震灾害的角度看,地震波能量ES正是地震研究人员需要特别关注的。
在传统的地震学研究中,通常根据一定的理论或经验模式,通过地震震级来估计地震波能量ES。2000年后,随着数字地震学的发展,可以利用宽频带数字地震资料直接测定地震波能量ES,并由此测定能量震级Me。
1986年,博特赖特和乔伊(Boatwright and Choy, 1986)提出利用数字化宽频带记录的远震P波测定地震能量的方法,美国地质调查局(USGS)国家地震信息中心(NEIC)采用他们的方法,测定全球范围内M >5.5中强震的辐射能量,进而得到能量震级Me,在NEIC常规产出的《震中初步报告》(Preliminary Determination of Epicenters,PDE)中列出能量震级Me。1998年,纽曼和奥卡尔(Newman and Okal, 1998)对博特赖特和乔伊的计算过程进行了简化,从而适用于大地震之后的准实时处理。2011年,康弗斯和纽曼(Convers and Newman, 2011)采用以上算法,测定了1990年以来全球MW≥6.0地震的能量和能量震级,并在美国地震学研究联合会(IRIS)的地震能量查询网站(http://www.iris.edu/spud/eqenergy)公布。
德国国家地球科学研究中心(GFZ)也在积极研究地震能量和能量震级的测定并付诸实践,吉亚科莫和汪荣江等(Giacomo et al,2008)提出浅源中强地震的能量震级Me的测定方法,利用震中距在20°—98°范围内的宽频带远震P波信号,测定浅源地震波能量ES和能量震级Me。由于各种原因,此项工作最终未在实际台网运行中得到应用。在吉亚科莫和汪荣江等(Giacomo et al,2008)的基础上,我们利用参考地球模型AK135Q(Kennett et al,1995)和QSSP(Wang,2009)来计算球形地球的格林函数,设计地震波能量测定软件,用于测定6.0级以上地震的地震波能量ES和能量震级Me。
1 地震波能量ES和地震矩M0地震波能量ES和地震矩M0是2个重要的物理量,目前是衡量地震大小最好的量,物理意义清楚。地震波能量ES是关于震源定量的特征量,地震以地震波形式辐射的能量主要集中在震源谱的拐角频率附近,对于地震灾害与风险评估,人们更关注的是地震辐射能量ES的大小,特别是其高频成分的地震辐射能量。地震矩M0是震源等效双力偶中一个力偶的力偶矩,是继地震波能量ES后的第2个关于震源定量的特征量,一个描述地震大小的绝对力学量,是反映震源区不可恢复的非弹性形变的量度。由此可见,地震矩是对断层滑动引起的地震强度的直接量度。所以M0由地震波振幅的低频成分大小决定,反映了震源处破裂的大小,断层面积越大,激发的长周期地震波的能量也越大,周期越长。因此,地震矩与地震所产生的断层长度、断层宽度、震源破裂平均位错量等静态的构造效应密切相关。地震波能量ES和地震矩M0之间的关系(Stein and Wysession, 2003)为
| $ \frac{{{E_{\rm{S}}}}}{{{M_0}}} \approx 5 \times {10^{ - 5}} $ | (1) |
| $ \lg {E_{\rm{S}}} = \lg {M_0} - 4.3 $ | (2) |
由式(1)可见,地震波能量ES与地震矩M0的量纲相同,若采用国际单位制(SI),其单位为焦耳(J)或牛顿·米(N·m)。虽然ES与M0的量纲相同,但物理意义不同,并且在数值上,地震波能量仅为地震发生时所释放地震矩的0.000 05(5×10-5)。这是因为,地震发生时释放的地震矩并非所辐射的地震波能量。虽然ES与M0的单位相同,但为了明确表示地震矩与地震波能量是性质不同的2个物理量,始终用牛顿·米(N·m)表示地震矩,用焦耳(J)表示地震波能量。另一方面,地震波能量是唯一能用地震学方法测量的物理量,在提到地震能量时,一般指地震波能量。
2 能量震级Me地震波在传播的过程中,质点具有一定的运动速度,从而将地震能量向远方传播。地震波所携带的能量ES包括地震波动能EK和地震波势能EW(万永革,2016),即
| $ {E_{\rm{S}}} = {E_{\rm{K}}} + {E_{\rm{W}}} $ | (3) |
对于某一固定频率的地震波,考虑到平面S波传播方向为x,位移方向为y,则S波质点运动位移为
| $ {u_x} = A\sin \left({\omega t - kx} \right) $ | (4) |
式中,ω = 2π/T,其中ω为角频率,T为地震波周期;A为地震波周期为T的位移的振幅;k = ω/β,其中k为波数,β为S波速度。则S波运动速度可以写为
| $ {{\dot u}_x} = A\omega \cos \left({\omega t - kx} \right) $ | (5) |
单位体积内地震波质点运动的动能,即动能密度为
| $ {e_{\rm{K}}} = \frac{1}{2}\rho \dot u_x^2 = \frac{1}{2}\rho {A^2}{\omega ^2}{\cos ^2}\left({\omega t - kx} \right) $ | (6) |
式中,eK为动能密度,ρ为地震台站处的介质密度。则平均地震波的动能密度为
| $ \begin{array}{l} \overline {{e_{\rm{K}}}} = \frac{1}{2}\frac{\rho }{T}\int_0^T {\dot u_x^2{\rm{d}}t} = \left({\frac{\rho }{{2T}}} \right)\left({\frac{{2{\rm{ \mathsf{ π} }}A}}{T}} \right)\\ \int_0^T {{{\cos }^2}} \left({\frac{{2{\rm{ \mathsf{ π} }}}}{T}t - kx} \right){\rm{d}}t = \rho {{\rm{ \mathsf{ π} }}^2}\frac{{{A^2}}}{{{T^2}}} \end{array} $ | (7) |
势能也称应变能,是恢复力(应力)作用下介质变形(应变)引起的。可以证明(万永革,2016),对于S波平均势能密度,有
| $ {{\bar e}_{\rm{E}}}\frac{1}{4}\rho {A^2}{\omega ^2} = \rho {{\rm{ \mathsf{ π} }}^2}\frac{{{A^2}}}{{{T^2}}} $ | (8) |
可以看出,S波的平均动能密度和平均势能密度相同,则平均能量密度为
| $ {{\bar e}_{\rm{S}}} = 2\rho {{\rm{ \mathsf{ π} }}^2}\frac{{{A^2}}}{{{T^2}}} $ | (9) |
同样可以证明,P波平均能量密度与S波相同,则
| $ {{\bar e}_{\rm{P}}} = 2\rho {{\rm{ \mathsf{ π} }}^2}\frac{{{A^2}}}{{{T^2}}} $ | (10) |
因此,P波和S波的平均能量密度具有相同形式。平均能量密度与地震波振幅的平方成正比,与地震波周期的平方成反比;对于同样的振幅,高频地震波携带能量更多。
由式(10)可见,地震波的平均能量密度与A2成正比。如果考虑球面波传播的几何校正,则地震波能量可以写为(Lay et al,1995)
| $ {E_{\rm{S}}} = F\left({r, \rho, c} \right){\left({\frac{A}{T}} \right)^2} $ | (11) |
式中,r为地震波传播距离,ρ为地震台站处的介质密度,c为地震波传播速度,A/T表示地震波质点运动速度,因此地震波能量ES与其质点运动速度的平方成正比。式(11)可以写成与震级相似的形式(Lay et al,1995),则
| $ \lg {E_{\rm{S}}} = \lg F\left({r, \rho, c} \right)+2\lg \left({\frac{A}{T}} \right) $ | (12) |
式(12)等号右边与震级M有关。在地方性震级ML、面波震级MS、体波震级mb和mB的计算公式中均有lg(A/T)项(中国大陆地方性震级ML的计算公式使用lgA,因为中国大陆地震基本属于板内浅源地震,S波或Lg波周期T为0.8—1.0 s)。lgF(r,ρ,c)与震级的量规函数有关。
古登堡和里克特(Gutenberg and Richter, 1954)得到震级和地震能量之间的关系,为
| $ \lg {E_{\rm{S}}} = a + bM $ | (13) |
式中,a与b为常量,古登堡—里克特的面波震级MS—能量关系式为
| $ \lg {E_{\rm{S}}} = 1.5{M_{\rm{S}}} + 4.8 $ | (14) |
对于短周期体波震级mb,古登堡—里克特短周期体波震级mb—能量关系式为
| $ \lg {E_{\rm{S}}} = 2.4{m_{\rm{b}}} - 1.2 $ | (15) |
式中,ES单位为焦耳(J)。
值得注意的是,震级和地震能量之间的经验关系式[式(14)或式(15)]仅是对地震能量的粗略估计,具有一定局限性,主要存在以下问题:①用震级推算地震能量,实际是一种“以偏概全”的结果。震级是针对比较窄的地震波频段的测定结果,如测定短周期体波震级mb,一般使用周期为1 s左右的地震体波信号,面波震级MS一般使用20 s左右周期的面波信号,而地震能量的测定则应考虑所有频段的地震波能量。不过,在模拟记录时代,由于观测条件的限制,只能使用这样一个粗略的关系;②由于震级存在饱和现象,mb的饱和震级为6.5,MS的饱和震级为8.5,对于较大的地震使用震级估计的地震能量会明显偏低。几乎很少使用式(15)估计地震能量,在实际工作中经常使用式(14)估计地震能量。
式(14)可以写成
| $ {M_{\rm{S}}} = \frac{2}{3}\left({\lg {E_{\rm{S}}} - 4.8} \right) $ | (16) |
将式(16)中的MS换成Me,即得新的震级标度Me的定义式,则
| $ {M_{\rm{e}}} = \frac{2}{3}\left({\lg {E_{\rm{S}}} - 4.8} \right) $ | (17) |
新的震级标度Me 称为能量震级(energy magnitude),是MS标度的自然延伸。
由于地震波的能量正比于地面运动质点速度的平方,在拐角频率fc处达到其最大值,地震能量主要集中在拐角频率附近。因此,能量震级适合用于反映地震灾害的程度。
3 能量震级测定 3.1 测定方法由公式(17)可知,若能测定地震波能量ES,则可以得到能量震级Me。
弹性波释放的能量与地面运动速度的平方成正比,假设地震的震源为点源,震源周围为均匀球面,则可以用远震P波的垂直向记录测定地震能量(Venkataraman and Kanamori, 2004a,2004b;Bormanm,2011)。
| $ {E_{\rm{S}}} = \left[ {\frac{1}{{15{\rm{ \mathsf{ π} }}\rho {\alpha ^5}}} + \frac{1}{{10{\rm{ \mathsf{ π} }}\rho {\beta ^5}}}} \right]\int\limits_{ - \infty }^\infty {{{\left| {\hat {\ddot M}\left(f \right)} \right|}^2}{\rm{d}}f} $ | (18) |
| $ {E_{\rm{S}}} = \left[ {\frac{2}{{15{\rm{ \mathsf{ π} }}\rho {\alpha ^5}}} + \frac{1}{{5{\rm{ \mathsf{ π} }}\rho {\beta ^5}}}} \right]\int\limits_{{f_1}}^{{f_2}} {{{\left| {\frac{{\dot u\left(f \right)}}{{^{G\left(f \right)}{/_{2{\rm{ \mathsf{ π} }}f}}}}} \right|}^2}{\rm{d}}f} $ | (19) |
式中,α、β和ρ分别为P波速度、S波速度和震源处介质密度;f为频率;f1、f2分别代表积分截取频率的最小值和最大值;
乔伊和博特赖特使用400多个地震的资料,导出新的ES—MS经验关系式(Choy and Boatwright, 1995),即
| $ \lg {E_{\rm{S}}} = 1.5{M_{\rm{S}}} + 4.4 $ | (20) |
在地震波能量计算的基础上,乔伊和博特赖特建立了能量震级Me的定义式,即
| $ {M_{\rm{e}}} = \frac{2}{3}\left({\lg {E_{\rm{S}}} - 4.4} \right) $ | (21) |
由式(18)、式(19)或其他可靠方法得到实测ES,即可由式(21)计算能量震级Me,该震级比按古登堡—里克特震级—能量关系式(14)计算得到的面波震级总体高0.27级(0.4/1.5)。
| $ {M_{\rm{e}}} = {M_{\rm{S}}} + 0.27 $ | (22) |
在吉亚科莫和汪荣江等(Giacomo et al,2008)工作基础上,利用参考地球模型AK135Q(Kennett et al,1995)和QSSP(Wang,2009)来计算球形地球的格林函数,设计地震波能量测定软件,用于测定6.0级以上地震的地震波能量ES,并对2015年以来国内6.0级以上地震、国外6.5级以上地震的能量震级Me进行了测定,测定结果将陆续公布。文中以2017年九寨沟7.0级地震和2013年芦山7.0级地震为例,通过对2个地震的面波震级MS和矩震级MW的对比,表明能量震级Me更能反映地震灾害程度。
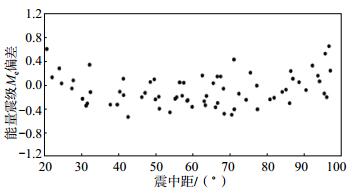
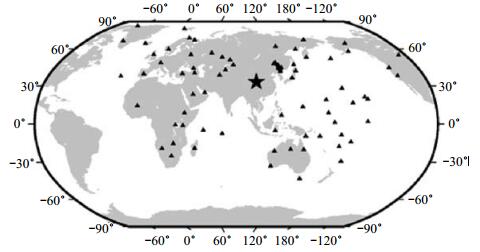
据中国地震台网测定,北京时间2017年8月8日,四川省阿坝州九寨沟县发生7.0级地震。利用全球地震台网(GSN)68个地震台站和中国国家地震台网的10个地震台站的宽频带地震记录,采用自行设计软件测定该地震的地震波能量和能量震级(李赞等,2019),得到能量震级Me为6.3。图 1给出单台能量震级与平均能量震级之间的偏差,其中横坐标为震中距Δ,纵坐标为单台震级与平均震级的偏差(震级偏差为-0.4—0.7)。由图 1可见,测定的每个台站的能量震级均在5.9—7.1,表明能量震级偏差与台站位置无关。能量震级计算所用地震台站分布见图 2,图中五角星表示震中位置,三角形表示台站位置。
|
图 1 九寨沟地震能量震级偏差分布 Fig.1 The deviation distribution for Jiuzhaigou earthquake energy magnitude |
|
图 2 九寨沟地震能量震级测定所用台站分布 Fig.2 The station distribution for Jiuzhaigou earthquake energy magnitude mensurration |
对于九寨沟地震,中国地震台网中心测定的面波震级MS为7.0,美国哈佛大学测定的矩震级MW为6.5,美国地震学研究联合会(IRIS)网站(http://ds.iris.edu/spud/eqenergy)发布的能量震级Me为6.4,我们测定的能量震级Me为6.3。中国地震局通过灾区震害调查、强震动观测记录分析、遥感航空影像震害解译等工作,确定此次地震的烈度分布,最高烈度为Ⅸ度,涉及九寨沟县漳扎镇,面积139 km2(http://www.cea.gov.cn)。对于2013年4月20日芦山地震,中国地震台网中心测定的面波震级MS同样为7.0,美国哈佛大学测定的矩震级MW为6.6,IRIS网站发布的能量震级Me为6.7,我们测定的能量震级Me为6.6,中国地震局发布的最高烈度为Ⅸ度,面积208 km2,Ⅸ度面积比九寨沟地震大69 km2。由此可见,对于面波震级MS同为7.0的2个地震,虽然矩震级MW大小基本相同,但由于能量震级Me相差0.3,造成的地震灾害差异就较大。
4 讨论与结论地震矩M0和地震波能量ES是2个重要的物理量,由地震矩M0可以得到矩震级MW,由地震波能量ES可以得到能量震级Me,2000年以后国际主要地震机构和许多国家的地震台网在日常工作中均可产出矩震级MW,但能量震级测定进展比较缓慢。
地震矩M0是一个静态物理量,与震源谱的低频渐近线有关,描述震源构造效应,对断层破裂的过程不敏感,所以M0由地震波振幅的低频成分大小决定,反映了震源处的破裂大小,断层面积越大,激发的长周期地震波能量也越大,周期越长。因此,矩震级与地震所产生断层长度、断层宽度、震源破裂的平均位错量等静态的构造效应密切相关。
地震波能量ES反映震源动态特征,与地震震源的动力学特性(如地震波频率、地震波速度等)密切相关。地震以地震波形式辐射的能量主要集中在震源谱的拐角频率附近,因此能量震级Me更适合描述地震的潜在破坏性。对于地震灾害与风险评估,人们更关注的是地震辐射能量ES的大小,特别是其高频成分的地震辐射能量。从断裂动力学、运动学以及地震所造成灾害的角度而言,地震能量与应力降、震源破裂速度密切相关。因此,联合测定矩震级MW和能量震级Me对于量化和评估地震灾害具有重要意义。
目前,我们正在对该方法进行实用化研究,若能够在震后15 min内准确测定能量震级,争取在地震台网的日常产出中测定能量震级,不断丰富地震台网的产出,为科学研究、地震灾害评估提供基础资料。
新的震级国家标准《地震震级的规定》(GB17740—2017)规定了地方性震级ML、短周期体波震级mb、宽频带体波震级mB(BB)、面波震级ΜS、宽频带面波震级ΜS(BB)和矩震级MW等6种震级的测定方法,待能量震级Me测定方法在地震台网的日常产出中得到应用,将形成完整的震级标准体系。
| 陈运泰, 刘瑞丰. 地震的震级[J]. 地震地磁观测与研究, 2004, 25(6): 1-12. DOI:10.3969/j.issn.1003-3246.2004.06.001 | |
| 李赞, 刘瑞丰, 孔韩东. 中强地震能量震级测定[J]. 地震学报, 2019(待刊) | |
| 万永革. 地震学导论[J]. 北京:地震出版社, 2016: 347-350. | |
| Boatwright J L, Choy G. Teleseismic estimates of energy radiated by shallow earthquakes[J]. J Geophys Res, 1986, 91: 2095-2112. DOI:10.1029/JB091iB02p02095 | |
| Bormann P. Earthquake magnitude[M]. In: Harsh Gupta (ed.). Encyclopedia of Solid Earth Geophysics, Springer, 2011: 207-218; doi: 10.1007/978-90-481-8702-7. | |
| Choy G, Boatwright J L. Global patterns of readiated seismic energy and apparent stress[J]. J Geophys Res, 1995, 100(B9): 18205-18228. DOI:10.1029/95JB01969 | |
| Convers J A, Newman V. Global evaluation of large earthquake energy from 1997 through mid-2010[J]. J Geophys Res, 2011, 116: B08304 | |
| Giacomo D, Grosser H, Parolai S, Bormann P, Wang R. Rapid determination of Me for strong to great shallow earthquakes[J]. J Geophys Res Lett, 2008, 35: L10308 | |
| Gutenberg B, Richter C F. Seismicity of the Earth and Associated Phenomena[M]. Princeton: Princeton University Press, 1954. | |
| Kennett B L N, Engdahl E R, Buland R. Constraints on seismic velocities in the Earth from traveltimes[J]. Geophys J, 1995, 122: 108-124. DOI:10.1111/gji.1995.122.issue-1 | |
| Lay T and Wallace T C. Modern Global Seismology[M]. ISBN 0-12-732870-X, Academic Press, 1995: 1-521. | |
| Newman A V, Okal E A. Teleseismic estimates of radiated seismic energy:The E/M0_discriminant for tsunami earthquakes[J]. J Geophys Res, 1998, 103: 26885-26898. DOI:10.1029/98JB02236 | |
| Stein S, Wysession M. An Introduction to Seismology, Earthquakes and Earth Structure[M]. Malden: Blackwell Publishing, 2003: 1-498. | |
| Venkataraman A, Kanamori H. Effect of directivity on estimates of radiated seismic energy[J]. J Geophys Res, 2004a, 109: B04301 DOI:10.1029/2003JB002548 | |
| Venkataraman A, Kanamori H. Observational constraints on the fracture energy of subduction zone earthquakes[J]. J Geophys Res, 2004b, 109: B04301 | |
| Wang R. A simple orthonormalization method for stable and efficient computation of Green's functions[J]. Bull Seismol Soc Am, 1999, 89(3): 733-741. |
 2018, Vol. 39
2018, Vol. 39
 ,
,