国内外历次强震震害调查结果表明，场地覆盖土层厚度、分布及土动力特性等场地条件，对地震动特性以及工程结构破坏程度影响显著。在强震作用下，软弱场地的地震动放大效应是造成边坡失稳、工程结构地基沉降、侧移以及结构倒塌的主要原因（Seed and Idriss, 1969；胡聿贤等，1980；齐文浩，2008）。在我国，特别是在地质条件复杂的江河下游、沿海海湾和近海软弱场地，软土和饱和土层分布广泛，场地条件对建筑结构的抗震不利。一旦发生地震，因场地效应引起的建筑结构与生命线工程的倒塌、失效，将造成严重的人员伤亡和财产损失。

场地效应在1976年唐山大地震、1985年墨西哥地震、1994年美国加州北岭地震、1995年日本阪神地震以及1999年中国台湾集集地震中均有所体现。学者们利用震害调查、试验论证、理论分析以及数值模拟等手段，开展了包括场地土类别、场地地形、地震强度等因素对地震动影响的研究工作，并取得较大进展（赵成刚，2006；杜修力等，2011；刘汉龙，2012；温瑞智等，2015）。近年来，为了加深理解场地条件与所观察地震动之间的相互影响，进一步提高反演土体线性/非线性动力参数精度，强震动观测钻井台阵被逐步建立、发展起来。自1933年美国在加州长滩地震中获得第一条地震加速度记录以来，各国学者开始了以强震动观测数据为基础的局部场地条件对地震动影响的研究工作。在过去的20年，随着强震动观测技术的发展，美国（CSMIP）、日本（KiK-net）、中国以及欧洲许多国家布设了大批钻井台阵，为充分了解实际应力状态下的场地震反应机制，理解局部场地地震动放大效应原理，完善数值模拟方法，分析复杂场地非线性地震反应，提供了强有力的数据支持。多年来，国内外科学家利用地震活跃地区的钻井台阵数据，包括美国Garner Valley和Treasure Island竖向钻井强震观测台阵（Finn et al，1993；Harichane et al，2005；Holzer and Youd, 2007；王海云，2014），日本Chiba，Port Island竖向钻井台阵（Katayama et al，1990；Yang et al，2000；Wen et al，2006），中国台湾Lotung（Elgamal et al，1995；Zeghal et al，1995；Chang et al，1996；Glaser and Baise, 2000；潘龙，2001；Borja et al，2002）和Hualien竖向钻井台阵（Chang et al，1996；Gunturi et al，1998；Glaser and Baise, 2000）以及唐山响嘡、通海（谢礼立等，1999；卢滔，2003；陈学良等，2007）等地区的竖向台阵，计算确定场地土层剪切波速度和谐振频率，识别场地非线性，对场地条件的影响做了大量理论分析和数值模拟。

鉴于强震动记录的不断增加、人们对土非线性动力特性本质认识的日益深刻以及计算方法的不断进步，利用非线性土动力本构研究场地地震反应成为趋势（Wen et al，1994；Beresnev and Wen, 1996）。李小军（1992）在Masing法则及Prke模型的基础上，提出土体动态骨架曲线模型，并结合显式差分数值逐步积分方法，推导出来一种求解非线性土层地震反应的方法，解决了等效线性化方法的窄频放大效应问题。栾茂田等（1992）利用Ramberg-Osgood和Hardin-Drnevich动力本构关系与广义Masing准则，考虑土在地震产生的不规则加载条件下的非线性滞变特征，将逐步积分法与不平衡荷载转移法相结合，建立了求解场地地震反应的非线性分析方法，能够较好地模拟不规则加载。卢滔等（2008）提出了一种考虑拟合阻尼比、刚度比试验曲线的时域分析方法，通过对比响嘡台阵场地土层地震一维非线性反应数值模拟结果与实际强震记录，验证了该方法的可行性。土层地震反应分析技术的深入研究，有助于进一步完善场地地震反应数值模拟方法，提高场地地震反应与地震动参数预测的精度。

在进行场地地震反应分析时，场地的剪切波速是定量估计场地条件影响的重要参数。如何更方便、更准确地得到场地剪切波速是地震工程研究者关注的课题。本文通过分析美国加州La Cienega钻井台阵收集的强震动记录，对所观测的地震动加速度幅值、反应谱等一系列工程特征进行分析，利用互相关函数提取可靠的场地土层平均剪切波速，以弥补试验研究中由于土体扰动、加载路径、场地分层、边界条件等因素造成的土动力特性分析结果偏差。此外，本文建立一维自由场地地震反应有限元分析模型，实现由场地非线性地震反应的定性分析到参数定量分析的过渡。

选取美国加州强震动观测计划（CSIMP，约38个钻井台阵）中深厚软弱场地（D类）上的24703号La Cienega钻井台阵（图 1）为研究对象，对该台阵所记录的地震动进行分析。La Cienega钻井台阵位于北岭地震中倒塌的莫尼卡高速公路（I-10）附近（图 1），共记录近20个1.9＜M＜7.1地震事件（包括自由场地、18.29 m和100.6 m等3个不同深度处3个分量的地震动），其中有4次事件记录了243.8 m深度处的地震动。本文所选取研究的13个地震事件（表 1，见http://www.strongmotioncenter.org/）与钻井台阵的震中距在4.3—57.3 km，震级范围3.3—5.4。其中，2001年9月9日W Hollywood M4.2地震事件，震中距4.3 km，水平峰值加速度达0.49 g。

图 1(Fig. 1)

图 1 24703台站俯视 Fig.1 Google Earth image of station 24703

表 1(Tab. 1

表 1 24703 La Cienega钻井台阵强震记录Tab. 1 Earthquakes recorded by station 24703 La Cienega geotechnical array 地震事件 日期 震级 震中距/km PGA/g W Hollywood 2001-09-09 ML 4.2 4.3 0.490 Inglewood 2009-05-17 MW 4.7 11.4 0.110 Encino 2014-03-17 MW 4.4 14.7 0.106 ViewPark-Windsor Hills 2015-04-12 ML 3.3 5.2 0.083 ViewPark-Windsor Hills 2015-05-03 ML 3.8 4.4 0.067 Inglewood Aftershock 2009-05-19 ML 4.0 12.4 0.053 LA Airport 2012-07-25 ML 3.7 8.4 0.034 Chino Hills 2008-07-29 MW 5.4 57.3 0.030 San Fernando 2001-01-13 MW 4.3 27.1 0.021 Westwood 2017-09-18 ML 3.6 10.6 0.021 Whittier Narrows 2010-03-16 ML 4.4 28.6 0.016 Marina Del Rey 2009-01-23 ML 3.4 10.3 0.012 Chatsworth 2007-08-09 ML 4.6 36.8 0.012 Lahabra 2014-03-28 M 5.1 44.2 0.012

表 1 24703 La Cienega钻井台阵强震记录 Tab.1 Earthquakes recorded by station 24703 La Cienega geotechnical array

场地的地震效应主要取决于覆盖土层厚度、土层剪切波速及阻尼3个基本要素。利用互相关函数计算强震动记录到时差方法，可以确定钻井台阵2个测点之间的平均剪切波速。在研究地震动剪切波在场地覆盖土层的竖向传播时，当地震波从深度i点传递到深度j点时，此2点不同深度处强震动加速度时程记录a_i(t)和a_j(t)之间的互相关函数C_aiaj(t)，将在2点之间时间延迟τ的位置上出现一个峰值，即当τ等于剪切波通过钻井台阵相邻2个加速度记录仪（距离为d）的时间时，2组信号的互相关函数为最大值。这里，描述2个时间序列a_i(t)和a_j(t)，在任意不同时刻nΔt和(n+m)Δt之间的相关程度可以用互相关函数C_aiaj(t)来表示，则

从而，钻井台阵2个测点之间的平均剪切波速（v_S）可由下式计算得到

式中，d为2个传感器之间的距离，峰值处对应的τ_d为相关函数所对应的地震波在相应2个传感器之间传播所需时间。

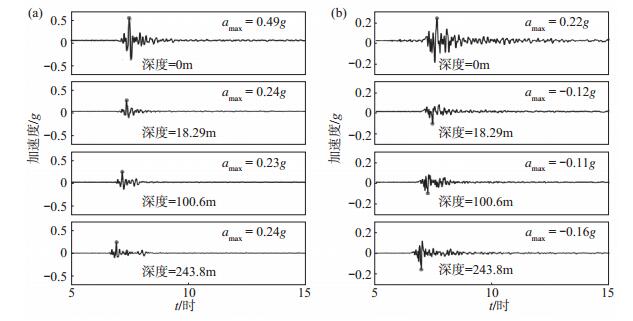
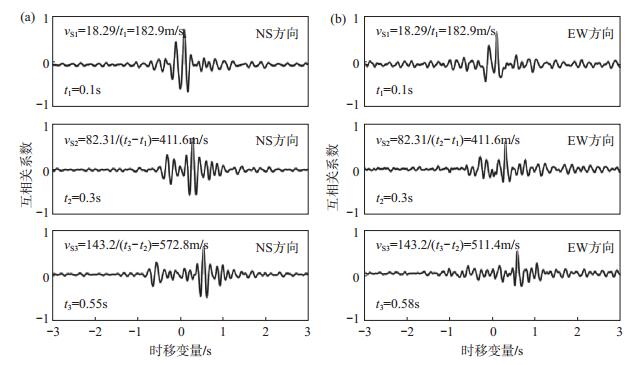
加州运输部和美国地质调查局提供的La Cienega钻井台阵钻孔剪切波速剖面及地质剖面资料见图 2，其中测点分别布设在地表 0 m及地表下18.29 m、100.6 m、243.8 m处，相应深度位置见图中黑点。由图 2可见，在地表附近，剪切波（S波）速度约150 m/s，在30 m深度增加至400 m/s。其中，2001年W Hollywood M_L4.2地震事件中4个测点不同深度处加速度时程（图 3）显示，地表加速度相当于其他深度处记录的2倍。以W Hollywood地震及4个小震（Marina Del Rey地震，2次ViewPark-Windsor Hills地震和Inglewood余震）为例，给出利用互相关函数的数据分析方法评估La Cienega钻井台阵测点间土层平均剪切波速的计算结果，见图 4、图 5，可见平均剪切波速随深度增加而加大。对于PGA较大的W Hollywood地震，0—18.29 m深度段土层平均剪切波速为v_S =182.9 m/s；由4个小震记录加速度时程平均互相关系数得到的平均剪切波速为215.2 m/s（图 5）。对于钻井台阵其他小震记录，由互相关函数法得到的平均剪切波速（v_S）在203.2—304.8 m/s区间，略大于W Hollywood地震的平均剪切波速。以上结果反映了地震作用下土层场地的非线性效应，可见在较大地震动发生时，土体波速会有更大程度的减小。

图 2(Fig. 2)

图 2 剪切波速剖面及测点位置 Fig.2 Shear wave velocity profile

图 3(Fig. 3)

图 3 2001年9月9日W Hollywood地震加速度时程记录 (a) NS分量；(b)EW分量 Fig.3 Recorded acceleration time histories during the W Hollywood earthquake on Sep. 9, 2001

图 4(Fig. 4)

图 4 2001年9月9日W Hollywood地震记录加速度互相关系数 Fig.4 Cross-correlation during the W Hollywood earthquake on Sep. 9, 2001

图 5(Fig. 5)

图 5 La Cienega钻井台阵记录的4个小震记录加速度时程平均互相关系数 Fig.5 Overall average cross-correlation based on the acceleration time histories of 4 small earthquakes

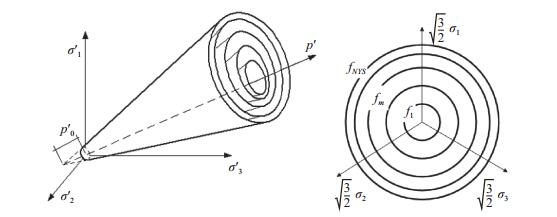
在使用数值模拟方法进行土层非线性地震反应评估时，其分析结果的准确程度主要取决于描述在地震作用下的非线性土体动力本构模型的可靠性以及场地模型参数的准确性。为了验证互相关函数识别的剪切波速度的准确性，选取La Cienega钻井台阵2001年W Hollywood M_L 4.2地震记录为研究对象，利用有限元程序Cyclic 1D建立一维自由场地地震反应分析模型。模型中土体本构采用与压力有关的多屈服面弹塑性模型。其中，土体的非线性剪切行为用一系列线段近似的剪应力—应变骨架曲线来描述（图 6）。此多屈服面土体本构模型已通过大量动三轴试验以及离心机试验验证其合理性。

图 6(Fig. 6)

图 6 与压力有关的多屈服面塑性土本构模型（Yang，2000；Yang et al，2003） Fig.6 Conical yield surface in principal stress space and deviatoric plane (Yang, 2000;Yang et al, 2003)

由图 3可知，该场地在地表下0—18.29 m土层段地震动放大明显，因此文中将有限元模型中地震动的输入位置设定在地表下18.29 m处。该场地模型共30个单元，其中多屈服面塑性土本构模型参考剪切波速取值以及由此得到的土体模型剪切波速随深度变化见表 2和图 2，阻尼比取为1%。

表 2(Tab. 2

表 2 Cyclic 1D一维有限元模型的土层特性Tab. 2 Soil layer properties of Cyclic 1D model 土层深度/m 土类别 土密度/kg·m-3 参考剪切波速/m·s-1 参考平均围压/kPa 围压指数系数 摩擦角 泊松比 0—18.29 砂土 2 000 228 90 0.52 40 0.4

表 2 Cyclic 1D一维有限元模型的土层特性 Tab.2 Soil layer properties of Cyclic 1D model

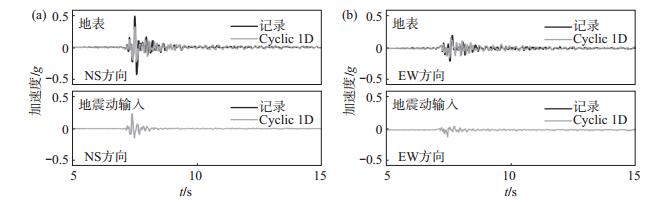
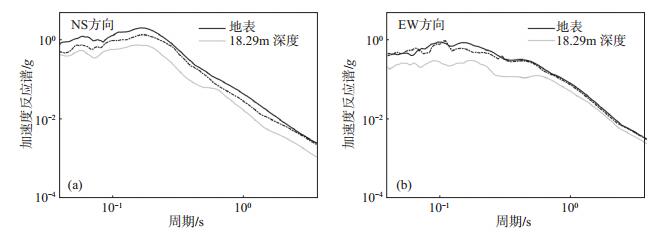
如图 7所示，Cyclic 1D计算结果与实际记录拟合较好，证明基于强震动记录互相关函数识别的土层平均剪切波速是可靠的。基于强震动记录识别的平均剪切波速计算结果的NS向地表地震动加速度反应谱（虚线）比实际记录的反应谱（实线）略低[图 8(a)]，EW方向地表地震动加速度反应谱计算结果与实际记录基本吻合[图 8(b)]。

图 7(Fig. 7)

图 7 地表处加速度记录与模拟计算值的比较 Fig.7 Comparison of acceleration time histories between results of Cyclic 1D and measurement

图 8(Fig. 8)

图 8 Cyclic 1D加速度反应谱与实测记录对比（实线基于实际记录，虚线为数值模拟结果） Fig.8 Comparison of response spectra between results of Cyclic 1D and measurements

本文以美国加州La Ciegena钻井台阵实测记录为基础，探讨了利用互相关函数分析方法反演场地浅层土体剪切波速度的有效性。用一维有限元方法对真实场地进行土层地震反应模拟分析，其计算结果与钻井台阵地震动记录基本一致，说明了本文所采用的方法的可行性。本研究表明，竖向钻井台阵强震动观测资料能够提供地震动过程中原状土体动力特性的重要信息，对于提高对土体动力特性的认识，分析场地效应具有重要意义。确定的土层特性很大程度上取决于传感器的可用性和间距。因此，由于传感器（位于地表以下18.29 m、82.31 m和143.2 m）之间的距离较大，本文对场地土体动力参数的空间分层变化的信息没有进一步区分。即便如此，估计的剪切波速度与美国地质调查局和加州交通局的井下剖面也有很好的一致性。