地震层析成像(Aki and Lee, 1976)是探测地球内部速度结构的重要方法之一,Zhao(2001)和Rawlinson等(2010)对该技术进行了系统总结。根据使用的地震波类型,地震层析成像可以分为体波和面波层析成像,其中面波层析成像主要用于全球范围大尺度研究;体波层析成像可以用于小尺度局部区域研究(Zhao,2001)。
地震走时层析成像基于一定的模型参数化和正演射线追踪方法。在对地球介质进行参数化时可分为离散介质和连续介质2种类型。离散化模型适应性强,走时计算和射线追踪方法健壮性好,但难以描述复杂构造的精细结构,且受计算机内存和运算速度影响较大。层状结构是常见的分段连续介质描述方法,该方法介质描述简单,模型基础上的正演射线追踪计算方便快捷(Zelt and Smith, 1992),但在描述逆断层等复杂三维地质体时变得困难,而块状结构描述则较为容易。Gjøystdal等(1985)首先提出三维块状建模概念,Pereyra(1996)发展了块状模型描述的技术;在块状建模基础上,采用三角形面片描述模型界面,在构建复杂模型方面有了较大提升,理论上可以构建任意复杂构造的地质体(徐涛等,2004;Xu et al,2006, 2008, 2010;李飞等,2013)。
运动学射线追踪方法包括试射法(Langan et al,1985;Sun,1993)和弯曲法(Julian and Gubbins, 1977;Um and Thurber, 1987)。试射法在全局搜索接收器方面效果较好,而弯曲法的计算效率较高。基于块状建模方法,发展了适用于常速度(Xu et al,2006)、常梯度速度(Xu et al,2010)以及任意非均匀速度分布(李飞等,2013;Xu et al,2014)介质中的逐段迭代射线追踪方法,对于传统的试射法,追踪效率显著提高。
本文基于三维块状建模以及快速高效的逐段迭代射线追踪方法,采用共轭梯度(Fletcher and Reeves, 1964)非线性反演算法,开展三维地质模型中的地震波走时反演研究工作。
1 三维复杂地质模型中的射线追踪针对网格结构和层状结构描述复杂地质模型时的困难,采用地质块组成的集合体描述三维地质模型,并用三角形面片描述块体之间的间断面。块状结构模型中,每个地质块定义有各自的地质属性,如地震波速度、密度等,并与其他地质块存在相邻边界(李飞等,2013)。在描述三维地质模型内部非均匀速度分布时,对地质体每个块体内部速度场单独定义,构建独立三维网格,并在网格节点上定义速度值(李飞等,2013;Li et al,2014)。
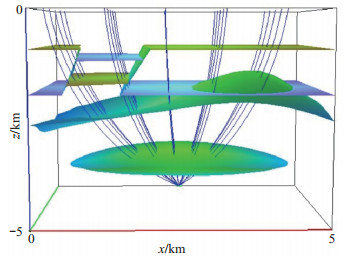
Um等(1987)提出伪弯曲法射线追踪,用于解决连续介质中的两点射线追踪问题。对于非均匀速度分布的三维地质模型,基于费马原理,发展逐段迭代射线追踪方法(李飞等,2013;Xu et al,2014)。该方法属于弯曲法的范畴,对射线路径点采用一阶显式增量修正,相对于传统迭代法(Zhao et al,1992),射线追踪更加高效、省时。联合逐段迭代法与伪弯曲法(Um and Thurber, 1987),提出一种连续三点的射线追踪扰动修正方案,可以适应三维复杂非均匀介质中存在速度间断面的层状模型和块状模型,且相对于传统的试射法和弯曲法具有更高的射线追踪效率(李飞等,2013;Xu et al,2014)。设计一个三维复杂块状模型,进行逐段迭代射线追踪试验,该模型在x,y,z方向的尺度均为5 km,包含正断层、逆断层、侵入体和透镜体等复杂构造,见图 1。
|
图 1 三维复杂块状模型中的射线追踪 Fig.1 Ray tracing in 3D complex blocked models |
综上,块状建模结合三角形界面可以构建任意复杂的三维地质体,快速高效的逐段迭代射线追踪适用于存在速度间断面的三维复杂模型,为三维地质模型中的地震波走时反演研究奠定了坚实的正演基础。
2 共轭梯度反演算法共轭梯度法(Fletcher and Reeves, 1964)不仅是求解大型线性方程组的有用方法之一,也是求解大型非线性最优化有效的算法之一。共轭梯度法可以看作是介于最速下降法与牛顿法之间的一种反演方法,具有以下优点:仅需利用一阶导数信息,既克服最速下降法收敛慢的缺点,又避免牛顿法需要存储和计算Hess矩阵并求逆的缺点,无须矩阵求逆以及保存n×n矩阵,对于二次型问题可以实现在n步内求解n个参数。所需存储量小,具有步收敛性,稳定性高,不需要外来参数。共轭梯度反演算法(Fletcher and Reeves, 1964)具体步骤为:①设定m为模型参量矩阵,目标函数φ为矩阵m的函数,k为迭代次数,第一次迭代取k = 0,设定模型初值m0;② g为一组线性无关的向量,第一次迭代设定初值g0=∇φ(m0),若g0=0,则迭代终止;③共轭方向向量p与线性无关向量g有关,H为Hess矩阵,为对称方阵,其阶数与需要反演的变量个数相同,变量
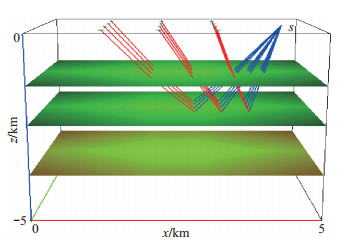
采用共轭梯度非线性反演算法,进行水平层状模型中介质速度与界面深度的地震波走时反演模型试验。如图 2所示,建立一个水平均匀的层状模型,模型在x,y,z方向的尺度均为5 km。定义第一、二层介质内的地震波速度分别为v1、v2,2层界面深度值分别为z1、z2(负值)。模型参量修正矩阵Δm中元素分别为Δv1、Δv2、Δz1、Δz2。
|
图 2 水平层状均匀模型及射线追踪结果 Fig.2 Horizontal stratified model and ray tracing results |
定义共轭梯度法走时反演的目标函数φ,则
| $ \varphi = \sum\limits_{\mathit{i}{\rm{ = 1}}}^n {\frac{1}{\mathit{n}}{{\left({{\mathit{T}_{{\rm{obs}}}} - {\mathit{T}_{{\rm{cal}}}}} \right)}^2}} $ | (1) |
式中n为接收器个数,Tobs为观测走时,Tcal为理论走时数据,以下类推。线性无关向量g为
| $ \mathit{\boldsymbol{g}}{\rm{ = }}\nabla \varphi ={\left({\frac{{\partial \varphi }}{{\partial {\mathit{v}_{\rm{1}}}}}, \frac{{\partial \varphi }}{{\partial {\mathit{v}_{\rm{2}}}}}, \frac{{\partial \varphi }}{{\partial {\mathit{z}_{\rm{1}}}}}, \frac{{\partial \varphi }}{{\partial {\mathit{z}_{\rm{2}}}}}} \right)^{\rm{T}}} $ | (2) |
目标函数φ分别对v1、v2、z1、z2求偏导,即可得到向量g中各元素的值。
结合上述水平层状均匀模型(图 2),Hess矩阵H应为对称方阵,其对应元素为目标函数φ分别对v1、v2、z1、z2的二阶偏导数,即
| $ \mathit{\boldsymbol{H}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\frac{{{\partial ^2}\varphi }}{{\partial \mathit{v}_1^2}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{v}_{\rm{1}}}\partial {\mathit{v}_{\rm{2}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{v}_{\rm{1}}}\partial {\mathit{z}_{\rm{1}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{v}_{\rm{1}}}\partial {\mathit{z}_{\rm{2}}}}}}\\ {\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{v}_{\rm{2}}}\partial {\mathit{v}_{\rm{1}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial \mathit{v}_2^2}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{v}_{\rm{2}}}\partial {\mathit{z}_{\rm{1}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{v}_{\rm{2}}}\partial {\mathit{z}_{\rm{2}}}}}}\\ {\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{z}_{\rm{1}}}\partial {\mathit{v}_{\rm{1}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{z}_{\rm{1}}}\partial {\mathit{v}_{\rm{2}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial \mathit{z}_1^2}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{z}_{\rm{1}}}\partial {\mathit{z}_{\rm{2}}}}}}\\ {\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{z}_{\rm{2}}}\partial {\mathit{v}_{\rm{1}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{z}_{\rm{2}}}\partial {\mathit{v}_{\rm{2}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial {\mathit{z}_{\rm{2}}}\partial {\mathit{z}_{\rm{1}}}}}}&{\frac{{{\partial ^2}\varphi }}{{\partial \mathit{z}_2^2}}} \end{array}} \right] $ | (3) |
共轭方向向量p的初值取为p0=-g0,并通过公式pk+1=-gk+1+βkpk进行更新;模型更新方式则为mk+1=mk+Δm,其中Δm=αkpk。经过一系列矩阵迭代运算,当向量g中各元素的值均小于某一精度的较小常数时,则认为迭代终止。
理论模型中2层介质速度值分别为4.8 km/s、5.4 km/s,2层界面深度值分别为-1.35 km、-2.4 km。建立如图 2所示的单炮记录观测系统,接收器均匀排列于地表,第2层底界面为地震波的反射界面。采用共轭梯度法分别进行简单层状模型中的介质速度反演和界面深度反演,反演结果随迭代次数的收敛曲线见图 3、图 4。从图中可以看出,一般经过数次迭代过程即可实现从初始模型收敛至逼近理论模型,且反演结果不受初始模型选择的影响。

|
图 3 共轭梯度法反演速度参数迭代拟合曲线 Fig.3 Fitting curve of velocity inversion with conjugate gradient method |

|
图 4 共轭梯度法反演深度参数迭代拟合曲线 Fig.4 Fitting curve of depth inversion with conjugate gradient method |
综上所述,块状建模结合三角形界面可以描述复杂的三维地质体,逐段迭代方法可以适应存在速度间断面的三维复杂块状模型中的快速射线追踪,共轭梯度非线性反演算法实现了三维层状模型中地震波走时反演,模型测试结果表明该地震波走时反演工作具有高效性。对于更为复杂的三维块状模型中非均匀速度分布与界面深度信息的联合反演成像工作,是本研究今后努力方向。
| 李飞, 徐涛, 武振波, 等. 三维非均匀地质模型中的逐段迭代射线追踪[J]. 地球物理学报, 2013, 56(10): 3514-3522. DOI:10.6038/cjg20131026 | |
| 徐涛, 徐果明, 高尔根, 等. 三维复杂介质的块状建模和试射射线追踪[J]. 地球物理学报, 2004, 47(6): 1118-1126. DOI:10.3321/j.issn:0001-5733.2004.06.027 | |
| Aki K, Lee W H K. Determination of three-dimensional velocity anomalies under a seismic array using first P arrival times from local earthquakes[J]. Journal of Geophysical Research, 1976, 81(23): 4381-4399. DOI:10.1029/JB081i023p04381 | |
| Fletcher R, Reeves C M. Function minimization by conjugate gradients[J]. The Computer Journal, 1964, 7(2): 149-154. DOI:10.1093/comjnl/7.2.149 | |
| Gjoystdal H, Reinhardsen J E, Åstebol K. Computer representation of complex 3-D geological structures using a new "solid modeling" technique[J]. Geophysical Prospecting, 1985, 33(8): 1195-1211. DOI:10.1111/gpr.1985.33.issue-8 | |
| Julian B R, Gubbins D. Three-dimensional seismic ray tracing[J]. Journal of Geophysics, 1977, 43: 95-113. | |
| Langan R T, Lerche I, Cutler R T. Tracing of rays through heterogeneous media:an accurate and efficient procedure[J]. Geophysics, 1985, 50(9): 1456-1465. DOI:10.1190/1.1442013 | |
| Li F, Xu T, Zhang M, et al. Seismic traveltime inversion of 3D velocity model with triangulated interfaces[J]. Earthquake Science, 2014, 27(2): 127-136. DOI:10.1007/s11589-013-0025-0 | |
| Pereyra. Modeling, ray tracing, and block nonlinear travel-time inversion in 3-D[J]. Pure and Applied Geophysics, 1996, 148: 345-386. DOI:10.1007/BF00874572 | |
| Rawlinson N, Pozgay S, Fishwick S. Seismic tomography:A window into deep earth[J]. Physics of the Earth and Planetary Interiors, 2010, 178(3/4): 101-135. | |
| Sun Y. Ray tracing in 3-D media by parameterized shooting[J]. Geophysical Journal International, 1993, 114(1): 145-155. DOI:10.1111/gji.1993.114.issue-1 | |
| Um J, Thurber C. A fast algorithm for two-point seismic ray tracing[J]. Bull Seismol Soc Am, 1987, 77(3): 972-986. | |
| Xu T, Li F, Wu Z B, et al. A successive three-point perturbation method for fast ray tracing in complex 2D and 3D geological models[J]. Tectonophysics, 2014, 627: 72-81. DOI:10.1016/j.tecto.2014.02.012 | |
| Xu T, Zhang Z J, Gao E G, et al. Segmentally Iterative Ray Tracing in Complex 2D and 3D Heterogeneous Block Models[J]. Bull Seismol Soc of Am, 2010, 100(2): 841-850. DOI:10.1785/0120090155 | |
| Xu T, Xu G M, Gao E G, et al. Block modeling and segmentally iterative ray tracing in complex 3D media[J]. Geophysics, 2006, 71(3): T41-T51. DOI:10.1190/1.2192948 | |
| Xu T, Zhang Z, Zhao A, et al. Sub-triangle shooting ray tracing in complex 3D VTI media[J]. Journal of Seismic Exploration, 2008, 17(2/3): 133-146. | |
| Zelt C A, Smith R B. Seismic traveltime inversion for 2-D crustal velocity structure[J]. Geophysical Journal International, 1992, 108(1): 16-34. DOI:10.1111/gji.1992.108.issue-1 | |
| Zhao D. New advances of seismic tomography and its applications to subduction zones and earthquake fault zones:A Review[J]. The Island Arc, 2001, 10(1): 68-84. DOI:10.1046/j.1440-1738.2001.00291.x | |
| Zhao D P, Hasegawa A, Horiuchi S. Tomographic imaging of P and S wave velocity structure beneath northeastern Japan[J]. Journal of Geophysical Research, 1992, 97(B13): 19909-19928. DOI:10.1029/92JB00603 |
 2018, Vol. 39
2018, Vol. 39
