0 引言

地震波非弹性衰减（Q值）和场地响应为近10年地震学重点研究方向之一（黄玉龙等，2003；刘杰等，2003；赵翠萍等，2004；华卫等，2010；马建新等，2015；叶庆东等，2016）。Q值做为研究震源性质的重要参数，在测定震源机制解、震源参数和估算震级等方面起到至关重要的作用（马建新等，2015），且地震波的衰减特征对于地震危险性分析具有重要意义, 是地震工程关心的基础资料之一。近年研究表明，岩石台基的台站场地效应并非都为1，即使非基岩台站，场地响应差别也可能较大（Shearer P M，1999；邹振轩，2006）；在非基岩台站中，场地的放大效应更加明显（王勤彩等，2004；高立新等，2005）。因此，想要得到精确参数，就必须区分地震记录中的震源效应、传播途径及场地效应。目前主要利用多台多震源联合反演方法（Atkinson，1992）计算地震波非弹性衰减特征（Q值），采用Moya等（2000）的遗传算法计算台站场地响应。

数字地震仪观测的地震运动记录包含震源、路径效应、仪器响应和观测噪音等信息（许英才等，2004）。数字地震观测具有动态范围大、观测精度高、分辨率高、系统传递函数特性更稳定、便于计算机处理等特点（许英才等，2004；梁向军等，2012）。随着数字地震观测技术的发展，震源机制的矩张量反演、地震噪声成像、地下结构反演等地震学结果得以产出并应用到地震预测等工作。

海南数字测震台网拥有22个测震台，利用数字化地震波形资料进行地震研究成为可能。本文使用海南数字地震台网记录的发生在海南岛及其附近海域的中小地震波形资料，采用互相衔接的三段几何衰减模型，通过频率域分析，研究海南岛剪切波的几何衰减和非弹性衰减以及场地响应特征。

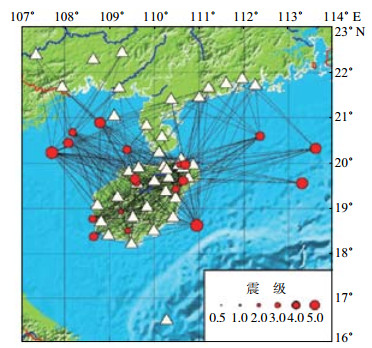
1 数字测震台网及资料选取 1.1 海南数字测震台网概况

海南数字测震台网1995年正式运行，当时由9个地震台站和1个中继站组成。“十五”期间地震台站密度增加，特别是海南西部和周边地区；对原有台站进行改造，设备、传输信道进行更新。目前，海南测震台网拥有22个测震台，其中2个为国家基准数字测震台、20个为区域数字测震台，主要沿海南岛边缘分布，琼东北地区地震台站分布较密，西南部地区较疏（图 1）。台间距最小为7.5 km，最大为100 km，考虑到新建地震台站记录资料时间短、完整性差等因素，仅对其中18个子台的台站响应进行反演（表 1）。

1.2 资料选取

通过地震目录和波形考察，选取2009—2014年海南及邻区（17°—23°N，106°—114°E）数字地震波形记录，采用“S窗”内包含所有可识别的S震相信号进行分析。要求参与计算的各地震台站有3次以上地震记录且每次地震有3条以上波形记录。根据以上条件，筛选出20个M_L介于2.0—4.1的地震事件（表 2）274条记录（图 1），用于反演18个子台的台站响应。

2 计算方法 2.1 Q值测定

经仪器响应校正后的地震波傅里叶谱振幅为

$ {A_{ij}}\left(f \right) = {A_{i0}}\left(f \right)G\left({{R_{ij}}} \right){{\rm{e}}^{ - \frac{{{\rm{ \mathsf{ π} }}f{R_{ij}}}}{{Q\left(f \right){v_{\rm{s}}}}}}}{S_j}\left(f \right) $

(1)

式中，A_ij为经过仪器响应校正的第j个台站记录到的第i个地震的傅里叶谱振幅，A_i0(f)为第i个地震的震源谱振幅，R_ij为第j个台站记录到的第i个地震的震源矩，G(R_ij)为几何衰减系数，Q(f)为品质因子，S_j(f)为第j个台站的场地响应，v_S为剪切波波速。对式（1）取对数，得

$ \log {A_{ij}}\left(f \right) = \log {A_{i0}}\left(f \right) + \log G\left({{R_{ij}}} \right) + \log {S_j}\left(f \right) - c\left(f \right){R_{ij}} $

(2)

式中，$c\left(f \right) = \frac{{\log \left(e \right){\rm{ \mathsf{ π} }}f}}{{Q\left(f \right){v_{\rm{S}}}}}$为非弹性衰减系数，c(f)与介质品质因子Q(f)的关系为：$Q\left(f \right) = \frac{{{\rm{ \mathsf{ π} }}f\log \left(e \right)}}{{c\left(f \right){v_{\rm{S}}}}}$。

S波几何扩散采用G(R)三段模型（Atkinson et al，1992），公式为

$ G\left(R \right) = \left\{ \begin{array}{l} {R^{ - {b_1}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;R \le {R_{01}}\\ R_{01}^{ - {b_1}}R_{01}^{ - {b_2}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{R_{01}} \le {R_{ij}} \le {R_{02}}\\ R_{01}^{ - {b_1}}R_{01}^{ - {b_2}}R_{02}^{ - {b_2}}R_{01}^{ - {b_3}}R_{02}^{ - {b_2}}\;R \ge {R_{02}} \end{array} \right. $

(3)

式中，b₁ = 1，b₂ = 0，b₃ = 0.5，R₁ = 1.5H，R₂ = 2.5H，H为地壳厚度。海南岛的地壳平均厚度取H = 29 km。根据Atkinson方法，可通过迭代反演求得非弹性衰减系数c(f)和台站的场地响应S_j(f)。残差定义为

$ {k_{ij}}\left(f \right) = \left[ {\log {A_{i0}}\left(f \right)} \right] - \overline {\log {A_{i0}}\left(f \right)} $

(4)

式中，$\overline {\log {A_{i0}}\left(f \right)} $为第i个地震的平均震源谱振幅，通过对记录到该地震的所有台站计算得到的结果求平均得到。

$ \overline {\log {A_{i0}}\left( f \right)} = \frac{{\sum\nolimits_j^{{n_i}} {\left[ {\log {A_{i0}}\left( f \right)} \right]{_j}} }}{{{n_i}}} $

(5)

式中，n_i为记录第i个地震的台站数。

非弹性衰减系数c(f)的求解式为

$ {\rm{sum = }}\sum {_i} \sum {_j\left| {{k_{ij}}\left(f \right)} \right|} $

(6)

具体计算步骤如下：①设定所有台站的场地响应为1（即不考虑场地响应），对给定的非弹性衰减系数c(f)，通过对台站记录进行几何扩散和非弹性衰减校正，得到相应地震的震源谱振幅，调整c(f)值大小，使各台站得到的同一地震的震源谱振幅残差最小；②利用得到的参数，根据$\log {S_i}\left(f \right) = \frac{{\sum\nolimits_j^{{m_j}} {{k_{ij}}\left(f \right)} }}{{{m_j}}}$求场地响应，式中，m_j为第j个台站记录的地震事件数；③将场地响应的计算值代入，重新计算c(f)，使残差总和sum极小，不断重复步骤①、②、③以缩小残差总和，通过反复迭代，可得到该地区非弹性衰减系数c(f)，进而得到介质的品质因子Q(f)。

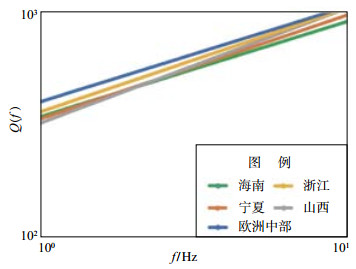
利用Atkinson法计算得到海南岛Q值，见图 2，可知海南岛Q值与频率具有以下关系：Q(f) = 343.7f^0.42。

2.2 利用Moya方法反演场地响应

Moya方法的原理在于，对每个地震选择Brune震源谱参数，计算已知地震的场地响应。

对第i个地震在第j个台站观测到的S波傅里叶振幅谱进行几何扩散时，采用三段几何衰减模型

$ A_{ij}^{{\rm{corr}}}\left(f \right) = {A_{ij}}\left(f \right)G\left({{R_{ij}}} \right)\exp \left({\frac{{{\rm{ \mathsf{ π} }}{R_{ij}}f}}{{Q\left(f \right)}}{v_{\rm{S}}}} \right)/{\left({2{\rm{ \mathsf{ π} }}f} \right)^2} $

(10)

式中，$A_{ij}^{{\rm{corr}}}\left(f \right)$为经过几何扩散和非弹性衰减校正得到的位移谱，${A_{ij}}\left(f \right)$为经过仪器响应校正的第j个台站记录到的第i个地震的傅里叶谱振幅，$G\left({{R_{ij}}} \right)$为几何衰减系数。

设定每次地震的震源谱参数（Ω₀和f_c），可得到每次地震的理论震源谱

$ A_i^{{\rm{theo}}}\left(f \right) = \frac{{{\mathit{\Omega }_{0i}}f}}{{1 + {{\left({\frac{f}{{{f_{ci}}}}} \right)}^2}}} $

(11)

在第k个频率上，第i个地震对第j个台站的场地响应为

$ {S_{ij}}\left({{f_k}} \right) = A_{ij}^{{\rm{corr}}}\left({{f_k}} \right)/A_i^{{\rm{theo}}}\left({{f_k}} \right) $

(12)

在第k个频率上，计算第j个台站由不同地震得到的场地响应平均值和标准偏差，则

$ {\delta _{jk}} = \frac{{{\rm{std}}{S_{ij}}\left({{f_k}} \right)}}{{{\rm{mean}}{S_{ij}}\left({{f_k}} \right)}} $

(13)

根据遗传算法，调整地震参数，使得δ_ik的和极小。

$ {\rm{sum = }}\sum\limits_i {\sum\limits_j {{\delta _{jk}}} } $

(14)

利用Moya方法计算海南岛18个地震台站的场地响应，计算结果见图 3，表明：各地震台站场地响应均与频率有关，在频率1—20 Hz范围内，场地响应因子范围为0.2—10。

3 海南岛Q值特征

利用Atkinson法计算得到海南岛Q值与频率的关系：Q(f)=343.7f^0.42。图 2给出海南岛、宁夏、山西、浙江以及欧洲中部Q值随频率关系的比较，其中宁夏Q(f)= 337f^0.4554、山西省Q(f)= 323f^0.506、浙江地区Q(f)= 361f^0.458、欧洲东部地区Q(f)= 400f^0.42。由图 2可见，本研究得到的海南岛Q值与频率的关系，与宁夏、山西、浙江及欧洲中部地区接近。与中国其他区域相比，海南岛Q值处于一个相对适中的范围。已有研究表明：在构造稳定地区，地震活动水平低，Q值高，地震波衰减慢；在构造不稳定地区，地震活动水平高，Q值低，地震波衰减快。如：Boatwright等（1991）认为，弧后盆地、洋中脊和构造活动区为低Q值区域；胡家富等（1999）研究得出：中朝准地台的地幔Q值明显低于稳定地区，而更加接近构造活动地区的Q值。

海南岛邻近环太平洋地震带，新近纪以来构造运动活跃，表现样式多样。在地壳间歇性上升背景下，发生强烈构造活动，在琼北形成火山岩台地和火山锥地貌，受EW向王五—文教断裂控制，断裂带南北两侧新构造运动表现形式不同，北面琼北断陷区表现为地震活动和剧烈的火山喷发，形成EW向展布的玄武岩被，南面五指山隆起区则主要表现为地热活动（张虎男等，1989）。根据刘昭蜀（2002）编制的南海及周缘地震区划图，海南省划归板内地震活动区，地震活动的特点是强度小、频度低、震源浅，震中分布随机性大。以上特殊的地质构造背景决定了海南岛相对适中的Q值。

4 海南岛台站场地响应特征

根据计算得到的海南岛Q值，利用多台多地震联合反演台站场地响应（Moya）方法，计算得到18个地震台站的场地响应，见图 3。由图 3可见，场地响应主要表现为4种变化特征，即：白沙、尖峰、陵水、七星岭4个子台的场地响应在1—20 Hz范围内接近1且变化平稳；白石岭、澄迈、定安、东方、那大、琼海、琼中、三亚、万宁、翁田、五指山11个子台的场地响应在1—20 Hz范围内小于1，变化平稳；青山岭和松林岭2个台站在低频部分衰减，在高频部分场地放大明显；沙坡台在低频部分接近1，在高频部分衰减。这种现象可能与海南岛复杂的地质构造背景有关。

长期以来，诸多学者根据海南岛EW向九所—陵水断裂带南北两侧古生代在沉积、变质、变形、古生物面貌等方面具有的明显差异性，以及王五—文教断裂带南北两侧新生代火山作用和沉积作用的差异性，对海南岛大地构造属性进行讨论。如：陈海泓等（1994）基于石碌群及晚古生代地层中发育的冰水沉积砾岩等，将海南岛纳入冈瓦纳大陆的范畴（莫宴情等，1987；虞子冶，1989）；汪啸风等（1991）认为海南岛结晶基底抱板群与云开地体中的云开群具有明显差异，提出海南岛晚古生代属于特提斯构造域范围的见解；许德如（2001）在研究元古代变质基性岩体的基础上，主张以NE向白沙构造带为界进行构造单元划分，与Metcalfe等（1994）以NE向构造进行海南岛大地构造单元划分的主张一致。以上研究表明：海南岛的板块块体、断裂带将其划分为不同构造区域，使该区非弹性衰减对场地响应产生较大影响。

海南区域数字地震台网18个台站因场地差异，不同频段所对应的台站场地响应差别较大。18个台站均布设在基岩上，但场地响应仍显示出一定差异性，说明区域地质条件对场地响应存在影响，因此在计算地震震源谱时必须考虑台站场地对地震波的影响，不能简单地取值为1。

5 结论

利用海南数字地震台网18个地震子台记录的274条波形资料，得到以下结论。

（1）采用多台多地震联合反演方法，得到海南地区Q值与频率的关系：Q(f) =343.7f^0.42。海南岛与宁夏、山西、浙江及欧洲东部地区的Q值相近，可能预示该区地质构造处于正常活动水平。

（2）18个台站的场地响应显示出4种特征，应与海南岛复杂的大地构造背景有关。

（3）由多台多地震联合反演台站场地响应（Moya）方法得到18个台站的场地响应，表明基岩台站的场地响应不能简单地取值为1，在计算震源谱时必须考虑台站的场地响应。