地震台网监测能力是衡量台网质量的重要指标。地震台网监测能力指台网监测本地微小地震并能够进行定位的能力,取决于地震台站的监测能力和布局(马强等,2015),而地震台站监测能力主要取决于台基噪声有效值。
目前,评估地震台网理论监测能力的常用方法是,基于近震震级公式,依据台基噪声有效值和指定震中距,估算各地震台站最小可监测震级,在不同地区,当至少有4个地震台站能够有效记录到地震时,该震级下限即可作为该地区能被地震台网监测到的最小震级,使用等值线将各地区连接起来,得到地震台网监测能力等值线图。有众多学者使用类似原理评估当地地震台站或台网的地震监测能力(孟智民等,2002;张黎珍等,2002;洪星等,2005;李雪英等,2005;郝春月等;2006;李涌等,2007;尹继尧等,2011;陈贵美等,2011;刘爱华等,2013;褚孝远等,2015;马强等,2015;陶方宇等,2015;陈健等,2016;王同军等,2016)。
镇江地区位于江苏南部,经济发展水平较高、人口密度大,如发生有感地震,社会影响较大。因此,有必要对镇江地区及周边地震进行有效监测。笔者旨在对镇江地震台网目前的地震定位能力进行估算与分析,确定镇江地震台网理论监测能力,为防震减灾事业服务。
1 镇江地震台网 1.1 镇江地震台镇江市地震台(下文简称镇江台)位于镇江市润州区官塘新城境内,属宁镇山脉地质条件,该山脉走向近EW,与主要地质构造走向以及河流流向基本一致,基岩为三叠系黄马青组砂岩。研究区域内主要分布凤凰河、幕府山—焦山、汤山—东昌、上党—河阳、丹徒—建山、丹阳—小河等断裂。
镇江台始建于1978年,属人工值守模拟地震台。1997年列入江苏省数字地震观测系统建设项目,新建177 m2办公用房和60 m2观测室,增添一套JC-V数字地震记录仪。镇江台配备CMG-3ESPC-60地震计,为地面摆,台基为砂岩,海拔34.0 m;数采型号为CMG-DM24 mk3,采样率为100 Hz;测震处理系统软件为JOPENS-0.4.3。测震信号通过流服务从本地服务器上传至江苏省地震台网中心服务器。
1.2 镇江地震台网镇江地震台网接收镇江、南京、六合、江宁、溧阳、溧水、泰州、金坛、常州、靖江等10个地震台站的测震信号,集地震监测、地震应急指挥、防震减灾科普教育为一体。其中,泰州台、溧阳台为井下摆。各台站参数见表 1。
| 表 1 镇江地震台网台站参数 Tab.1 Parameters of the sub-stations of Zhenjiang Seismic Network |
镇江地区地处华北地震区长江下游—黄海地震带,属中强地震活动带。根据《中国历史强震目录(公元前23世纪—公元1911年)》(国家地震局震害防御司,1995)、《中国近代地震目录(公元1912年—1990年,M≥4.7)》(中国地震局震害防御司,1999),镇江行政区域共发生4次破坏性地震(M≥4.7),分别为1630年2月4日4级地震、1872年7月24日4级地震、1913年4月3日M 5.5地震、1930年1月3日M 5.5地震;根据中国地震台网地震目录,自1970年以来,镇江行政区域共发生82次ML 1.0以上地震,其中ML 1.0—1.9地震43次、ML 2.0—2.9地震32次、ML 3.0—3.9地震7次。据统计,该区上一次破坏性地震为1930年1月3日M 5.5地震,至今未发生4级以上地震。
3 计算方法测定地方性震级ML应使用仿真成DD-1短周期地震仪两水平向记录S波(或Lg波)的最大振幅,计算公式为
| $ {M_{\rm{L}}} = \lg A + R\left( \mathit{\Delta } \right) $ | (1) |
式中,A=(AN + AE)/2,单位μm,其中AN为NS向S波或Lg波最大振幅(单位μm),AE为EW向S波或Lg波最大振幅(单位μm);Δ为震中距,单位km;R(Δ)为地方性震级的量规函数。其中,S波峰值振幅为位移量,而测震台站记录数据为地动速度,需进行换算。
台基噪声在较窄频带(1—20 Hz)内进行计算,精度要求不高,可用简单方法换算速度幅值与位移幅值,换算时取S波的优势频率为3—5 Hz,本文取3.5 Hz,初动震相波形有效值与台基噪声有效值En之比,是能否检测到一个可能地震事件的重要参数,本文以a表示。水平向S波振幅与初动震相峰值之比,本文以b表示,初动震相峰值与初动震相波形有效值之比,本文以c表示。由此,可以通过台基噪声有效值En计算满足检测限地震事件的水平向S波振幅,即a×b×c×En。
为检测到一个地震事件,a值通常取3—4,本文取3;b值取为3;对于地方震,c值通常在2.5—3.5范围内,本文取3。因此,S波振幅为27×En。代入近震震级公式,得
| $ {M_{\rm{L}}} = \lg \left( {\frac{{3 \times 3 \times 3 \times {E_{\rm{n}}} \times 1000000}}{{2 \times {\rm{ \mathsf{ π} }} \times 3.5}}} \right) + R\left( \mathit{\Delta } \right) \approx \lg \left( {{E_{\rm{n}}}} \right) + R\left( \mathit{\Delta } \right) + 6.1 $ | (2) |
其中En单位为m/s(中国地震局监测预报司,2017)。
通过公式(2)、起算函数R(Δ)、水平向台基有效噪声值,可以得到测震台站最小可监测震级与震中距的关系,即为测震台站监测能力,由此评估地震台网监测能力,步骤如下:①对监测区域进行网格划分,网格间距取平均台间距的1/3。在每个网格节点上,以该节点与台网中每个测震台站的距离为震中距,依据台基噪声,按照上述公式,分别计算各台站在该节点处能够监测到的最小震级,并存储在该节点的相关数组中;②若台网中有N个台站,则上述计算完成后,每个节点有N个数据,从小到大排序,保留第4个震级代表台网对该节点的可监测震级下限;③依据每个节点的震级值,绘制震级等值线图。
4 数据处理选择江苏省及邻区(29°—36°N,115°—125°E)作为地震监测区域,计算该区地震台网监测能力。对该区域进行网格划分,网格间距取平均台间距的1/3(平均台间距使用每个台站到最近3个台的数据),即30个数据取平均值(不剔除重复计算数据)。设2点经纬度坐标为:A(WA,JA),B (WB,JB),根据大地坐标系与直角坐标系的换算关系(孔祥元等,2001),得
(1)设A点直角坐标为(XA,YA,ZA),则
| $ \begin{array}{l} {X_{\rm{A}}} = \frac{{a\cos {W_{\rm{A}}}}}{W}\cos {J_{\rm{A}}}\\ {Y_{\rm{A}}} = \frac{{a\cos {W_{\rm{A}}}}}{W}\sin {J_{\rm{A}}}\\ {Z_{\rm{A}}} = \frac{{b\sin {W_{\rm{A}}}}}{V} \end{array} $ | (3) |
(2)设B点直角坐标为(XB,YB,ZB),则
| $ \begin{array}{l} {X_{\rm{B}}} = \frac{{a\cos {W_{\rm{B}}}}}{W}\cos {J_{\rm{B}}}\\ {Y_{\rm{B}}} = \frac{{a\cos {W_{\rm{B}}}}}{W}\sin {J_{\rm{B}}}\\ {Z_{\rm{B}}} = \frac{{b\sin {W_{\rm{B}}}}}{V} \end{array} $ | (4) |
其中,a为椭圆长半轴,b为椭圆短半轴,W、V为含椭圆偏心率的辅助函数,因研究区域较小,将地球考虑为正球体而非椭球体,W和V取值为1,在式(3)、式(4)中a、b为地球半径,因只参与弧度计算,将a、b假设为1。
设AB弧长即地面A、B两点间的球面距离为Δ,则
| $ \mathit{\Delta } = R \times C = R \times \arccos \left( {\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}} \right) $ | (5) |
其中C为OA与OB直线间夹角(弧度),R为地球半径(R=6 371.004 km),a为A点到球心的距离,b为B点到球心的距离,c为A、B两点间直线距离,则
| $ {c^2} = {\left( {{X_{\rm{A}}} - {X_{\rm{B}}}} \right)^2} + {\left( {{Y_{\rm{A}}} - {Y_{\rm{B}}}} \right)^2} + {\left( {{Z_{\rm{A}}} - {Z_{\rm{B}}}} \right)^2} $ | (6) |
台站间距计算结果见表 2。
| 表 2 各台至最近3个地震台的球面距离 Tab.2 The spherical distance between each station to the nearest three stations |
计算得到平均台间距为49.7 km,
| 表 3 起算函数R (Δ)(修改后) Tab.3 R(Δ) (Modified) |
台基噪声使2016年6月至2017年5月江苏省测震台网中心测定的数据中值,计算方法如下:以各台站3个分向每小时连续记录数据为样本,采用WELCH方法在全频段计算信号的加速度功率谱,按1/8倍频为单位间隔滑动地计算每条样本的平均功率谱。在(-200—-60)dB范围内以1 dB单位间隔计算整月各频率点上的分布概率。
选用10个地震台站各月水平向噪声水平最大值lg(RMSmax) + 6.1取平均值,设lg(RMSmax) + 6.1 = Xmax,计算结果见表 4。
| 表 4 各月Xmax值及均值 Tab.4 Xmax and monthly average Xmax |
选用10个地震台站各月水平向噪声水平小值lg (RMSmin) + 6.1取平均值,设lg(RMSmin) + 6.1=Xmin,计算结果见表 5。
| 表 5 各月Xmin值及均值 Tab.5 Xmin and monthly average Xmin |
由表 5可以看出,由不同台站噪声数据极大值和极小值计算得到的X值有0—0.3的差值,单独使用极大值或者极小值计算均会有所偏颇。因此,取Xmax与Xmin的均值X,即
| $ X = \frac{{{X_{\max }} + {X_{\min }}}}{2} = \lg \left( {{\rm{RMS}}} \right) + 6.1 $ | (7) |
计算结果见表 6。
| 表 6 各月X值及均值 Tab.6 X and monthly average X |
将X代入近震震级公式(2),得
| $ {M_{\rm{L}}} = X + R\left( \mathit{\Delta } \right) $ | (8) |
由式(8)得到各网格节点在各个台站的最小震级,对每个节点的10个数据从小到大排序,取其中第4个震级做为台网对该节点的可监测震级下限,使用此286个数据绘制震级等值线,得到镇江地震台网理论监测能力图,见图 1。
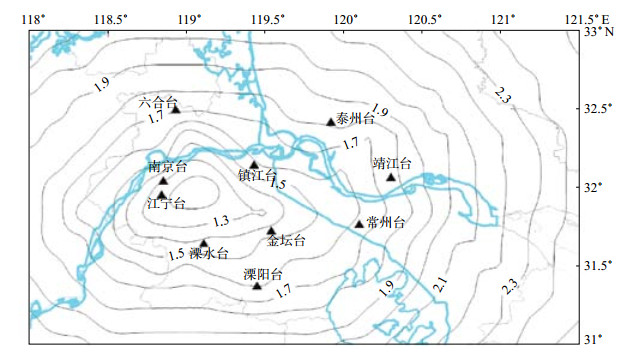
|
图 1 镇江地震台网监测能力 Fig.1 Monitoring capability of Zhenjiang Seismic Network |
为验证镇江地震台网理论监测能力,选取2016年6月1日至2017年5月30日镇江台记录并能够分析编目的22条地震,验证理论地震监测能力的可靠性,见图 2,图中圆圈代表达到4个及以上有效记录台数的地震,叉代表少于4个有效记录台数的地震。

|
图 2 理论震级与实测震级对比 Fig.2 Comparison of theoretical magnitude and measured magnitude |
有效记录台数是指地震信号符合上文所述地震记录信噪比≥3、S波振幅为P波振幅3倍以上的地震台站。若某一个地震震级因未达到理论监测震级导致低于4个有效记录台数,或者某一个地震震级高于理论监测震级而有4个及以上有效记录台数,则代表符合理论;否则不符合理论。如:2016年6月8日江苏南京ML 1.3地震未达到理论有效监测震级且只有3个台站的有效记录,2016年6月10日镇江丹阳ML 2.6地震达到理论有效监测震级且有8个台站的有效记录,2种情况中理论与实际相符;2017年2月11日安徽滁州市天长市ML 2.1地震达到理论有效监测震级,但只有3个台站的有效记录,则判定为理论与实际不符。
据以上判定原则,图 2中给出的22条编目地震有21条符合理论监测值,实测震级与理论震级相符率为95%。
6 结论综上所述,可知:①镇江地震台网监测能力优势分布偏向于镇江以西地区,最小地震监测能力并不位于镇江市人口密集区,而是镇江句容市,其有效监测震级低,为ML 1.2—1.3;②镇江市区及南京市区地震监测能力较好,为ML 1.3—1.4;③镇江大港扬中地区及南京浦口区地震监测能力稍差,为ML 1.4—1.6。因此,对于镇江及相邻城市,若发生ML1.8以上地震,镇江地震台网均可进行有效监测。
| 陈贵美, 康英, 杨选. 广东"十五"数字测震台网地震监测能力分析[J]. 华南地震, 2011, 31(3): 70-77. | |
| 陈健, 仇中阳, 刘江斌, 等. 淮安数字测震台网地震监测能力分析[J]. 地震地磁观测与研究, 2016, 37(1): 70-75. | |
| 褚孝远, 韩进, 杜瑶, 景晟. 雅砻江流域下游梯级水库地震台网监测能力验证[J]. 华南地震, 2015, 35(1): 57-61. | |
| 国家地震局震害防御司. 中国历史强震目录(公元前23世纪-公元1911年)[M]. 北京: 地震出版社, 1995. | |
| 郝春月, 郑重, 郭燕平, 等. 中国数字地震台网(CDSN)和IMS/PS台阵的监测定位能力评估[J]. 地震地磁观测与研究, 2006, 27(2): 56-63. | |
| 洪星, 杨贵. 福建数字地震台网对泉州地震的监测能力[J]. 地震地磁观测与研究, 2005, 26(2): 89-96. | |
| 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 武汉大学出版社, 2001, 33-37. | |
| 李雪英, 张新东, 胡斌. 河北省数字遥测地震台网的监测能力[J]. 山西地震, 2005, 11061106(2): 22-24. | |
| 李涌, 张艺, 戴仕贵. 阿坝州数字地震台网的动态范围与台网监控能力计算[J]. 四川地震, 2007, 11061106(4): 37-41. | |
| 刘爱华, 刘英华, 郝永梅, 等. 黑龙江省测震台网监测能力评估[J]. 地震地磁观测与研究, 2013, 34(3/4): 113-117. | |
| 孟智民, 王卫东, 李大伟. 陕西数字地震台网的监测能力[J]. 西北地震学报, 2002, 24(2): 178-182. | |
| 陶方宇, 陆栋梁, 王飞, 刘莉. 金寨地震台数字地震仪的监测能力分析[J]. 高原地震, 2015, 27(3): 47-51. | |
| 王同军, 陈凯, 舒涛, 等. 重庆三峡测震台网子台站地噪声及监测能力分析[J]. 内陆地震, 2016, 30(1): 49-55. | |
| 尹继尧, 朱元清. 上海数字地震台网监测能力评估[J]. 地震研究, 2011, 34(4): 476-481. | |
| 张黎珍, 胡翠娥, 李传江. 赣南遥测数字地震台网监测能力估算[J]. 华南地震, 2002, 22(4): 34-38. | |
| 中国地震局监测预报司. 测震学原理与方法[M]. 北京: 地震出版社, 2017. | |
| 中国地震局震害防御司. 中国近代地震目录(公元1912年-1990年, MS ≥ 4.7)[M]. 北京: 中国科学技术出版社, 1999. |
 2018, Vol. 39
2018, Vol. 39