2. 中国河北 065200 防灾科技学院
2. Institute of Disaster Prevention Sanhe, Hebei Province 065200, China
2011年3月11日日本本州东海岸附近海域发生9.0级地震,造成巨大灾害,是日本有地震记录以来震级最大一次地震。日本地处欧亚板块、菲律宾板块、北美板块和太平洋板块边界地带,是世界上著名的地震活跃区域之一。
通过对日本及其邻区1927—1966年发生的地震震源机制解进行研究,Honda等发现,日本海沟地区震源深度大于100 km的地震,主压应力方向与贝尼奥夫带走向大致垂直(Honda et al,1952, 1957)。Uyeda和Nakamura认为,日本海沟地区处于近东西向挤压应力状态,且随着向西远离海沟而逐渐减小(Uyeda et al,1979;Nakamura,1980)。宁杰远和臧绍先(1987)通过研究日本本州北部至中国东北地区的地震震源机制解,发现中国东北地壳应力场方向与日本海沟一致,应力均来源于太平洋板块的挤压。
日本9.0级地震发生后,国内外学者利用高频GPS、强震观测、宽频带地震波等资料,反演地震的破裂过程,并进行同震位移计算(Simons et al,2011;Yoshida et al,2011;周月玲等,2016;李姜等,2017;吕国军等,2017),其中王连捷等(2013)对日本9.0级地震引起的同震位移场和应力场进行了计算,并给出同震位移和应力分布。学者们对此次地震引起的主应力变化研究相对较少,而同震应力场对研究地震机理和重建震前应力场具有一定意义(Yamashita et al,2004)。
近年来,随着各种计算机自动处理系统的不断改进,日本在全国范围内设立宽频带高密度、高精度地震观测网,除琉球群岛等少数偏远岛区外,日本陆地以及近海海域的地震活动均得到监控,即使是极微小地震活动也能被记录下来,并能准确定位(徐纪人等,2003;吕国军等,2017)。由此,为探明日本9.0级地震发生机制积累了大量可靠的基础数据,使得本研究在现阶段成为可能。本文对日本9.0级地震前后不同时段震源机制解进行分析,以期为科学地预测地震的发生时间和地点提供依据。
1 应力场反演方法利用震源机制解反演构造应力场的方法,快速简单,且结果较为可靠,是当今地震学界公认的求解应力场的有效途径之一(胡幸平等,2008)。研究地壳和上地幔的应力状态对于了解板块运动和区域变形是有帮助的,本文使用震源机制来反映不能直接测量的地壳应力状态。
构造应力反演是一个非线性问题,通过网格搜索应力场参数的震源机制反演方法(以下简称FMSI法)来确定日本9.0级地震周围的主应力轴方向。FMSI法有3个基本假设(Gephart and Forsyth, 1984;Gephart,1990):①断层的滑动平行于牵引力的切线方向;②在考虑的岩石范围内,应力场是均匀的;③地震发生在先前存在的断层。该FMSI法使用网格搜索应力场参数区域来寻找最佳拟合模式,最大限度地减少可能的模型预测和实际数据之间的差别。
在FMSI中,为每个地震计算的个别不适合的参数被定义为任何方向的最小旋转角,得到3个主应力轴σ1、σ2和σ3(σ1≥σ2≥σ3)的方位角和倾伏角及比值R(0≤R≤1)的关系,即R = (σ2-σ3)/(σ3-σ1),可以帮助区分应力场类型。
在FMSI反演算法中有4种压力参数(σ1,σ2,σ3和R),每一次用于反演的事件数量为4,然而不同的数据集可以更好地约束,从而找出合适的应力张量方向。对于上述原因,使用每个数据集所有地震的震源机制得到当地应力场,而不用将一个区域的断层进行分类。
对FMSI程序,确定最佳应力模型步骤如下:①进行粗略网格搜索(应力方向以10°为间距)以覆盖整个范围的可能模式,称为粗略应力场反演法(英文缩写为FMSIA);②把由此产生的最好应力模型作为初始应力模型进行精确网格搜索(沿应力方向以5°为间距),称为精确FMSI方法(英文缩写为FMSIE)。在FMSI中,平均失配大小对应的最佳拟合应力模型可能是一个压力均匀度的反应指标。Wyss和Gillard进行了一系列试验,对于真正的地震,震源机制若有15°的残差就不能获得大于6°的应力场反演平均残差,因此平均残差小于6°可以代表均匀应力场(Lu et al,1997)。与此相反,平均残差大于9°表明了应力的非均质性。在应力残差为6°—9°时,应力解是可以接受的,但也可能反映了一些非均质性(Lu et al,1997)。
2 研究数据本研究使用日本防灾科学技术研究所(NIED)记录的此次9.0级地震数据和美国哈佛大学全球矩心矩张量(GCMT)数据资料库的矩张量反演估算震源机制解。其中,NIED数据提供的P波初动极性数据由日本气象厅(JMA)获取,或从东北大学地震观测网和Hi-net原始地震记录中获取。受获取数据途径的限制以及其他客观因素的影响,本研究使用日本海沟和陆地发生的浅源地震(< 30 km)资料,空间范围为(38°—39°N,140°—142°E),时间范围为2005—2010年。GCMT数据:由美国哈佛大学提供日本本州东海岸附近海域地震前后震源机制数据,覆盖(34°—42°N,136°—142°E)的区域,时间跨度为2006年—2011年12月。
根据P波初动的GCMT数据,利用ISFM_ftest程序(Wan et al,2016)可以求出综合断层面解。断裂应力状态与断层取向与滑动方向有关,选取多个走向、倾角和滑动角,运用ISFM_ftest程序求解日本9.0级地震前后应力场。
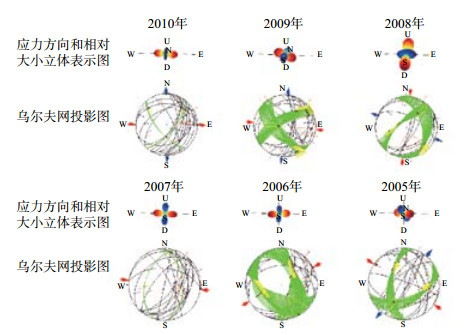
3 地震前后应力场演化 3.1 NIED数据地震前应力场演化根据NIED数据,绘制日本9.0级地震前应力场变化,见图 1,具体数值变化见表 1。由图 1可见,可以看出,2005—2010年震前应力场的挤压应力大部分在水平方向上,比较均衡稳定,而拉张应力比较复杂,方向不确定;2008年应力场变化稍显异常,挤压应力偏于垂直方向;2005—2010年大部分震源机制呈现逆断层和走滑断层类型。其中2010年和2007年的P轴、B轴、T轴走向和俯角的分辨率较高,节面约束较好,2010年的P轴不确定范围为:方位角89.12°—92.48°,俯角1.63°—3.81°,2007年的P轴不确定范围为:方位角94.19°—97.69°,俯角0.48°—1.48°(表 1)。
|
图 1 根据NIED数据日本9.0级地震前应力场变化 Fig.1 Stress field changes before the 9 magnitude earthquake in Japan based on NIED data |
| 表 1 根据NIED数据日本9.0级地震前应力轴变化 Tab.1 Stress axis changes before the 9 magnitude earthquake in Japan based on NIED data |
图 1中应力方向和相对大小立体表示图清晰可见挤压应力和拉伸应力的方向变化;乌尔夫网投影图中绿色为节面,黄色代表节面方向,红色箭头表示挤压应力,蓝色箭头表示拉张应力,其中蓝色小箭头代表观测方向,红色小箭头代表理论方向。
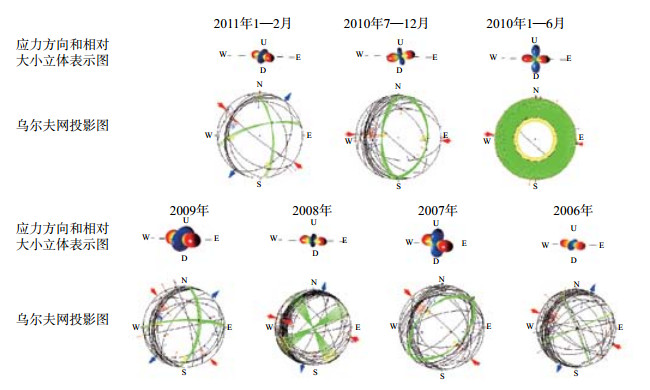
3.2 GCMT数据地震前后应力场演化选用GCMT数据绘制震前震源机制图,见图 2,应外力轴具体变化数值见表 2,可以看出,挤压应力也在水平方向,但稍有偏转,拉张应力方向较难判断,与选用NIED数据绘制的震前震源机制图基本一致。
|
图 2 根据GCMT数据日本9.0级地震前应力场变化 Fig.2 Stress field changes before Japan M 9 earthquake based on GCMT data |
| 表 2 根据GCMT数据日本9.0级地震前应力轴变化 Tab.2 Stress axis changes before Japan M 9 earthquake based on GCMT data |
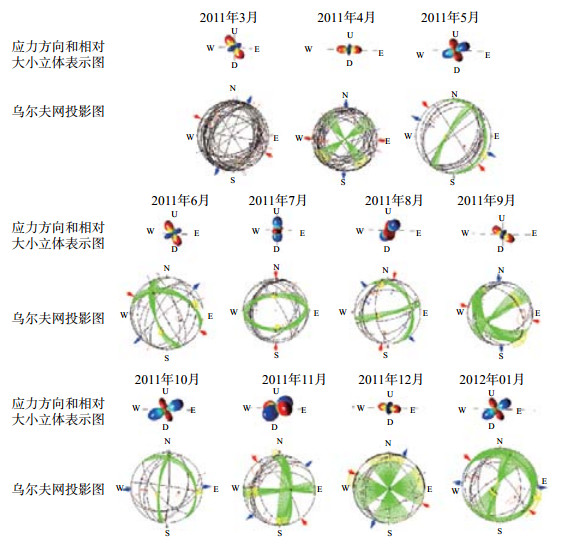
从震后震源机制图(图 3)可看出,因为大地震的发生,余震频繁,应力松弛,造成构造应力场发生变化,具体变化数值见表 3,表现为:2011年3月为走滑断层类型,4月挤压应力趋于水平,5月和6月挤压应力发生变化,为正断层类型,7月和8月为逆断层类型,9月为正断层类型,11月为走滑断层类型,说明挤压应力轴和拉张应力轴均不稳定。
|
图 3 根据GCMT数据日本9.0级地震后应力场变化 Fig.3 Stress field changes after Japan M 9 earthquake based on GCMT data |
| 表 3 根据GCMT数据日本9.0级地震后应力轴变化 Tab.3 Stress axis changes after Japan M 9 earthquake based on GCMT data |
根据NIED数据和GCMT数据,由震源机制给出的B、T、P应力轴倾俯角plug最大值,判断震源机制破裂类型。如Pplug最大,即P轴直立或接近直立,则认为属于正断层破裂类型;如Tplug最大,即T轴直立或接近直立,则认为属于逆断层破裂类型;如Bplug最大,则认为属于走滑断层破裂类型。
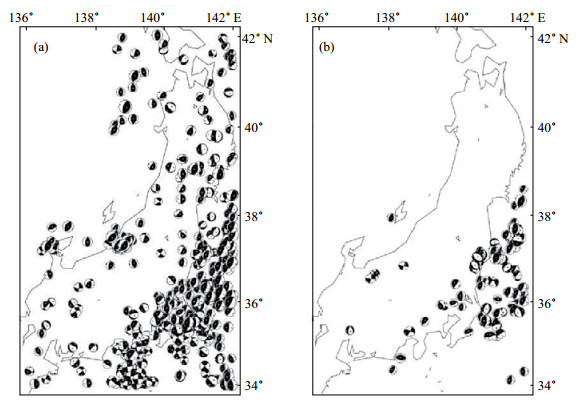
2011年3月11日日本9.0级地震震中(38.1°N,142.6°E)位于日本本州东海岸附近海域,将此次9.0级地震前后震源机制解震源球绘于地图中,见图 4,可以更好地分辨应力变化方向。图中,震源球的黑色区域是T轴区,即挤压区,白色区域是P轴区,即拉伸区。由图 4可见,此次9.0级地震前以走滑断层和逆冲断层破裂为主,主要分布在日本东南部。与地震前的逆断层与走滑断层型震源机制相比,图中的走滑型或正断层型机制解有明显变多趋势,主要分布在日本东南部,由此反演的区域应力场必然属于正断层类型。
|
图 4 日本9.0级地震前后震源机制解 (a)震前;(b)震后 Fig.4 Focal mechanism solution before and after Japan M 9 earthquake |
对2011年日本9.0级地震,利用FMSI震源机制反演法得到震中区域震源机制,进而分析求解此次地震前后日本内陆地区东部应力场。
选取NIED数据和GCMT数据进行分析,可得出,震前应力场的挤压应力接近水平向,比较均衡稳定,而拉张应力比较复杂,方向不确定。分析可知,日本东南部2005—2010年大部分震源机制呈现逆断层和走滑断层类型,且地震前应力场挤压应力接近水平,表明该地区地震以逆断层和走滑断层为主。2011年日本9.0级地震发生后,在日本东北地区的东南部,应力场发生变化,地震以正断层为主。
| 胡幸平, 俞春泉, 陶开, 等. 利用P波初动资料求解汶川地震及其强余震震源机制解[J]. 地球物理学报, 2008, 51(6): 1711-1714. | |
| 李姜, 张合, 周月玲, 等. 河北阳原-蔚县盆地地震灾害损失评估[J]. 华北地震科学, 2017, 35(3): 73-78. | |
| 吕国军, 李红梅, 康江, 孙丽娜. 河北省地质钻孔资料分析[J]. 地震地磁观测与研究, 2017, 38(2): 125-131. | |
| 吕国军, 张合, 李皓, 孙丽娜. 邢台地区设定地震事件烈度影响[J]. 地震地磁观测与研究, 2017, 38(4): 37-44. | |
| 宁杰远, 臧绍先. 日本海及中国东北地震的深度分布及其应力状态[J]. 地震地质, 1987, 9(2): 49-61. | |
| 王连捷, 王红才, 王薇, 等. 日本MW 9.0级地震同震位移场和应力场的有限元模拟[J]. 地球学报, 2013, 34(6): 665-670. DOI:10.3975/cagsb.2013.06.03 | |
| 徐纪人, 赵志新, 河野芳辉, 等. 日本南海海槽地震区域应力场及其板块构造动力学特征[J]. 地球物理学报, 2003, 46(4): 488-494. | |
| 周月玲, 郭秋娜, 孟立朋, 等. 深井盆地南缘断裂特征与活动性研究[J]. 震灾防御技术, 2016, 11(4): 747-755. DOI:10.11899/zzfy20160405 | |
| Gephart J W, Forsyth D W. An improved method for determining the regional stress tensor using earthquake focal mechanism data:application to the San Fernando earthquake sequence[J]. J Geophys Res, 1984, 89(B11): 9 305-9 320. DOI:10.1029/JB089iB11p09305 | |
| Gephart J W. FMSI:A fortran program for inverting fault/slickenside and earthquake focal mechanism data to obtain the regional stress tensor[J]. Comput Geosci, 1990, 16(7): 953-989. DOI:10.1016/0098-3004(90)90105-3 | |
| Honda H, Masatsuka A. On the mechanisms of the earthquakes and the stresses producing them in Japan and its vicinity[J]. Ibid, 1952, 4: 42-60. | |
| Honda H, Masatsuka A, Emura K. On the mechanism of the earthquakes and stresses producing them in Japan and its vicinity(second paper)[J]. Geophys, 1957, 8(3): 186-205. | |
| Lu Z, Wyss M, Pulpan H. Details of stress directions in the Alaskasubduction zone from fault plane solutions[J]. J Geophy Res, 1997, 102(B3): 5 385-5 402. DOI:10.1029/96JB03666 | |
| Nakamura K, Uyeda S. Stress gradient in arc-back arcregions and plate subduction[J]. J Geophys Res, 1980, 85(B11): 6 419-6 428. DOI:10.1029/JB085iB11p06419 | |
| Simons M, Minson S E, Sladen A, et al. The 2011 magnitude 9.0 Tohoku-Oki earthquake:Mosaicking the meganthrust from seconds to centuries[J]. Science, 2011, 332(6 036): 1 421-1 425. | |
| Uyeda S, Kanamori H. Back-arc opening and the mode of subduction[J]. J Geophys Res, 1979, 84(B3): 1 049-1 061. DOI:10.1029/JB084iB03p01049 | |
| Wan Yongge, Sheng Shuzhong, Huang Jichao, Li Xiang, Chen Xin. The Grid Search Algorithm of Tectonic Stress Tensor Based on Focal Mechanism Data and Its Application in the Boundary Zone of China, Vietnam and Laos[J]. Journal of Earth Science, 2016, 27(5): 777-785. DOI:10.1007/s12583-015-0649-1 | |
| Yamashita F, Fukuyama E, Omura K. Estimation of Fault Strength:Reconstruction of Stress before the 1995 Kobe Earthquake[J]. Science, 2004, 306(5 694): 261-263. | |
| Yoshida K, Miyakoshi K, Irikura K. Source process of the 2011 off the Pacific coast of Tohoku earthquake inferred from waveform inversion with long-period strong-motion records[J]. Earth Planets and Space, 2011, 63(7): 577-582. DOI:10.5047/eps.2011.06.050 |
 2018, Vol. 39
2018, Vol. 39
