ML震级标度简单、实用的特性使其至今仍是测定中小地震最为常见的震级标度。目前河北省地震台网测定近震震级ML,使用短周期量规函数R1(Δ)(杨晶琼等,2016)。量规函数是近震震级测量中地震波振幅(或位移)沿传播途径衰减变化的补偿值,是地震波随距离增大而衰减的平均量度,也是地震波区域衰减特征的一个定量描述。
中国地域辽阔,不同地区的地壳厚度和结构差别较大,加之震源深度的不同,导致量规函数存在差异,在云南地区与华北地区测定的ML就明显不同,区域特征明显,没有可比性。使用的量规函数不合适,则近台和远台(在仪器相同、台基相似条件下)对同一地震求出的地震震级不同(陈培善等,1983)。量规函数描述了地震波随震中距衰减的特性,与地壳构造紧密相关(薛志照,1992),因此,对区域性差异较大的地区,采用同一个量规函数显然不合理(严尊国等,1995),有必要建立分区近震量规函数。
由于地壳构造的复杂性和不均匀性,使地震波通过地壳传播变得复杂,加上各种因素的影响,计算ML震级使用的量规函数存在区域性特点,在河北地震台网使用统一量规函数会造成ML震级计算的离散性和不稳定性(孟晓琴等,2008)。针对河北地震台网近震ML震级,推荐使用分区量规函数R11(Δ)(新量规函数)。本文在ML原始定义的基础上,收集大量地震观测资料,使用分区量规函数重新计算ML震级,与使用旧量规函数的河北地震台网近震震级进行对比,分析分区量规函数的适用性和准确性。
1 资料选取“十五”期间,河北省地震局通过改建、升级和新建,形成覆盖京津及周边地区的数字地震观测台网。截至2016年底,河北地震台网接收本省及周边省、市168个地震台站数据,台站分布见图 1。地震数据采集器字长24位,采样频率100 Hz,采用基于数据库和分布式网络环境的JOPENS台网中心处理系统,进行数据接收、存储、交换和实时处理、交互分析、统一编目和归档等工作,积累了大量地震观测资料,为推广地方性震级的分区量规函数创造了良好条件。

|
图 1 河北地震台网台站分布 Fig.1 Distribution of seismic stations in Hebei Seismic Network |
为保证地震数据质量,按以下原则对原始数据进行筛选:①每个地震不少于6个地震台站的定位(包括单台)数据;②震源深度 < 5 km;③定位残差 > 0.5。为此,选取2008—2016年河北及周边地区ML 0.1以上地震目录、震相数据共计1 714组。其中,0.1—1级地震550个,1.1—2级地震537个,2.1—3级地震473个,3.1级以上地震154个。利用分区量规函数,重新计算所选地震ML震级,分析震级偏差,讨论分区量规函数的适用性。
2 计算方法1959年,李善邦先生(1981)将震级公式ML引入中国。
| $ {{M}_{\text{L}}}\text{ }\!\!~\!\!\text{ }=\text{ lg}\mathit{A}~+~\mathit{R}(\mathit{\Delta })\ \ \ \ \ \ (\mathit{\Delta }~<\text{ }1\ 000\ \text{km}) $ | (1) |
式中,
陈培善和秦嘉政(1983)改进得到震级残差统计分析法,即使用单台地震震级减去该地震的平均值得到单台地震的震级偏差,利用震级公式得到新的量规函数。具体步骤如下。
(1)设Ne为地震次数,Ns为记录地震的台站数,根据式(1),求得第i次地震第j个台站的单台震级MLij(陈运泰等,2004)。
| $ {{M}_{\text{L}\mathit{ij}}}\text{=lg}\left(\frac{{{A}_{\text{E}}}+{{A}_{\text{N}}}}{2} \right)\text{ }\!\!~\!\!\text{ }+{{\mathit{R}}_{\text{1}}}(\mathit{\Delta })\ \ \ \ \left(i=1, 2, \cdots, {{N}_{\text{e}}};j==1, 2, \cdots, {{N}_{\text{s}}} \right) $ | (2) |
(2)计算所有台站记录的第i次地震的震级平均值MLi,为
| $ {{M}_{\text{L}\mathit{i}}}=\frac{1}{{{N}_{\text{s}}}}=\sum\limits_{j=1}^{{{N}_{\text{s}}}}{{{M}_{\text{L}\mathit{ij}}}}\ \ \ \left(i=1, 2, \cdots, {{N}_{\text{e}}};j==1, 2, \cdots, {{N}_{\text{s}}} \right) $ | (3) |
(3)将式(2)减去式(3),得到单台震级偏差值ΔMLij,即
| $ \begin{align} \Delta {{M}_{\text{L}\mathit{ij}}}={{M}_{\text{L}\mathit{ij}}}-{{M}_{\text{L}\mathit{i}}}\ \ \ \left(i=1, 2, \cdots, {{N}_{\text{e}}};j==1, 2, \cdots, {{N}_{\text{s}}} \right) \\ \end{align} $ | (4) |
由单台震级偏差值可得到震级偏差ΔMLij随震中距Δ的变化曲线,如果量规函数正确,则震级偏差随震中距的变化曲线应在0值上下摆动,曲线偏差值的负值为量规函数的校正值,将校正值加到旧量规函数R1(Δ)上,即可得到分区量规函数R11(Δ)(新量规函数),具体数值见表 1。
| 表 1 分区量规函数 Tab.1 Partition gauge function |
河北地震台网记录的地震主要集中在震中距600 km以内,在此范围内,分区量规函数(新量规函数)与旧量规函数有一定变化,对比曲线见图 2。由图 2可见:震中距在0—130 km范围内,新旧量规函数坡度变化较大,均呈线性增长,且偏差基本大于0,即河北地震台网分区量规函数R11(Δ)比旧量规函数R1(Δ)偏大;震中距在130—270 km范围内,R11(Δ)与R1(Δ)增长缓慢,无太大波动,且二者大小基本一致;震中距大于270 km时,R11(Δ)与R1(Δ)变化比较复杂,在其中的几个震中距分段范围内,出现R11(Δ)与R1(Δ)基本持平现象,但2个量规函数偏差普遍小于0,即R11(Δ)比R1(Δ)偏小。

|
图 2 旧量规函数与分区量规函数对比曲线 Fig.2 Compared curves of old gauge function and partition gauge function |
(1)统计结果。为了检验分区量规函数的精度和可靠性,使用原有量规函数和分区量规函数,利用JOPENS系统提供的单纯型定位法、HYP2000或Hyposat法,对2008—2016年所选1 714个ML≥0.1地震进行重新定位,得到2种ML震级,并对比分析震级偏差和标准误差,结果见图 3。
|
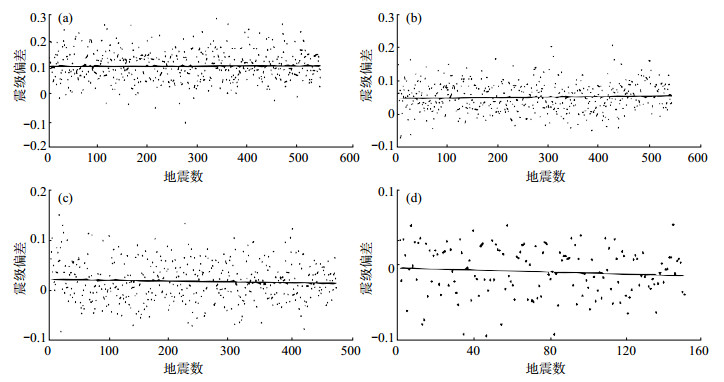
图 3 河北地震台网各震级段新旧量规函数计算的震级偏差 (a) 0.1≤ML≤1地震;(b)1.1≤ML≤2地震;(c)2.1≤ML≤3地震;(d)ML≥3.1地震 Fig.3 Magnitude deviation calculated by new and old gauge functions for each magnitude segment of Hebei Seismic Network |
从图 3可见:对于0.1≤ML≤1地震,新旧量规函数震级偏差的动态范围在-0.1—0.3,平均值约0.1;对于1.1≤ML≤2地震,新旧量规函数震级偏差的动态范围在-0.25—0.2,平均值约0.05;对于2.1≤ML≤3地震,新旧量规函数震级偏差的动态范围在-0.2—0.25,平均值约0.15;对于ML≥3.1地震,新旧量规函数震级偏差的动态范围在-0.1—0.2,平均值约-0.005。因此,采用分区量规函数计算地震震级,与原有量规函数所算震级差值变化不大,且偏差分布较为集中,满足河北地震台网震级精度要求。
(2)抽样结果。在所选地震中抽取7个震级样本计算单台震级与平均震级偏差,统计结果见表 2。
| 表 2 新旧量规函数计算的抽样地震单台震级均差和标准差 Tab.2 Average deviation and standard deviation of sampled seismic magnitude of single station with new and old gauge functions |
从表 2可知,对抽样地震使用分区量规函数计算的单台ML震级,与原量规函数计算结果相比,单台ML震级均差和标准差更小,说明使用分区量规函数得到的单台震级结果较好,可见使用分区量规函数能提高近震震级的测定精度。选取其中6个地震绘制单台震级偏差随震中距的变化关系图,见图 4,可见:在震中距0—100 km范围内,单台震级偏差基本小于0;在震中距100—200 km范围内无太大波动;在震中距大于300 km时,单台震级偏差基本大于0。

|
图 4 单台震级偏差随震中距的变化 Fig.4 Variation of magnitude deviation of single station with epicentral distance |
采用分区量规函数与原量规函数,计算并对比分析河北地震台网记录的ML≥0.1地震震级,得到以下结论。
(1)分区量规函数R11(Δ)与R1(Δ)相比,在0≤Δ≤100 km范围内数值较大,在100≤Δ≤200 km范围内二者偏差较小,在Δ ≥300 km时R11(Δ)数值偏小。
(2)使用分区量规函数R11(Δ)得到的ML震级标准误差比原量规函数R1(Δ)的标准误差小,说明R11(Δ)比R1(Δ)更适合河北地震台网,更能反映河北地区地壳构造特点。
(3)在计算的1 714组地震中,分区量规函数R11(Δ)与河北地震台网使用原量规函数计算的ML震级偏差在±0.1之间的有1 556个,占比约91.8%,二者结果一致性较好,能较好地衔接数据记录。
| 陈培善, 秦嘉政. 量规函数、台站方位、台基及不同测量方法对近震震级的影响[J]. 地震学报, 1983, 5(1): 87-98. | |
| 陈运泰, 刘瑞丰. 地震的震级[J]. 地震地磁观测与研究, 2004, 25(6): 1-12. | |
| 李善邦. 中国地震[M]. 北京: 地震出版社, 1981, 120-156. | |
| 孟晓琴, 梁向军, 张玲, 等. 山西地震台网速报震级与量规函数的研究[J]. 山西地震, 2008, 11061106(2): 19-23. | |
| 薛志照. 近震震级ML量规函数和台站校正值[J]. 华北地震科学, 1992, 10(1): 60-65. | |
| 严尊国, 李普丽, 薛军蓉. 中国近震震级量规函数检验研究[J]. 华南地震, 1995, 15(1): 1-11. | |
| 杨晶琼, 杨周胜, 蔡明军. IASPEI宽频带面波震级与传统面波震级的对比[J]. 地震研究, 2016, 39(2): 303-307. |
 2018, Vol. 39
2018, Vol. 39