2. 中国北京 100045 中国地震台网中心
2. China Earthquake Networks Center, Beijing 100045, China
由于地震过程的复杂性与地震波传播路径介质的复杂性,地震产生的地面震动的幅度和频率范围都很大。由地震所产生的地面位移的振幅,小可到纳米(1 nm = 10-9 m),大可到10 m,跨越11个数量级,而频率跨越约7个量级,即从周期达104 s的固体潮、103 s的地球自由振荡、102 s的长周期面波、10 s的长周期体波,到1 s的短周期体波、震中地区10-1 s的强地面运动和10-2 s地壳的小地震(陈运泰等,2000)。
震级是通过测量地震波中的某个震相的振幅来衡量地震的相对大小的一个量,由于不同类型地震辐射地震波的优势周期不同,并非所有地震都可以用同一把“尺子”来量度,对于传统的地方性震级、体波震级和面波震级来讲,不可能使用单一震级标度来定量描述所有地震的大小。最直接的办法是使用不同的震级标度描述不同地震的基本特征,这就是震级的多样性。
在新的强制性国家标准《地震震级的规定》(GB17740—2017)(以下简称新国标)中规定了地方性震级ML,短周期体波震级mb,宽频带体波震级mB(BB),面波震级MS,宽频带面波震级MS(BB)和矩震级MW等6种震级的测定方法,不同的震级实际反映了地震波在不同周期范围内辐射地震波能量的大小。地方性震级ML的优势周期在0.8 s左右,短周期体波震级mb的优势周期约1.0 s,面波震级MS的优势周期约20 s;宽频带面波震级MS(BB)和宽频带体波震级mB(BB)则充分发挥了宽频带数字地震资料的特点,适用的面波和体波周期范围明显增大,MS(BB)的周期范围为3—60 s,mB(BB)的周期范围为0.2—30 s。因此,对于大小不同的地震使用不同的震级标度更能客观表示地震的大小。
由于不同的震级标度使用不同周期和不同波列,而不同周期和不同波列所携带的来自复杂震源过程的信息不同。使用不同的震级标度,可以表示不同地震之间的差异,能够更加客观地表示地震的大小,从而描绘出形态各异、丰富多彩的地震世界。在全球各个国家的地震监测工作中,无论是在地震观测报告还是数据库中,给出的都是实际测定的震级值。金森博雄(Kanamori,1977)、普尔卡鲁和贝克汉姆(Purcaru and Berckhemer, 1978)以及汉克斯和金森博雄(Hanks and Kanamori, 1979)提出矩震级标度MW以后,由于矩震级是一个描述地震绝对大小的力学量,不存在震级饱和问题,目前矩震级已成为世界上大多数地震台网和地震观测机构优先使用的震级标度。但对于历史地震,已无法使用现代方法直接测定矩震级MW,美国地质调查局2002年制订的“美国地质调查局震级的发布规则”(USGS,2002)中明确规定,需使用地震现场的宏观调查信息(如断层面的大小、地面破坏等宏观资料)来确定历史地震矩震级MW,而不能使用传统的地方性震级ML,短周期体波震级mb,面波震级MS经简单换算得到。
在全球地震监测工作中,原始测定的震级之间一律不允许相互转换。
1 国家标准《地震震级的规定》(GB17740—1999)为了规范地震震级的测定和社会应用,1999年在许绍燮院士的带领下,由中国地震局地球物理研究所等单位的专家完成了国家标准《地震震级的规定》(GB17740—1999)的编制工作,该标准于1999年4月26日首次发布(许绍燮等,1999)。
鉴于当时国际地震中心(ISC)、美国地质调查局(USGS)国家地震信息中心(NEIC)、中国地震局(CEA)、日本气象厅(JMA)等国际地震机构在震级测定方法上存在的差别,尚未取得共识。我国大陆地震主要是板内地震,均属于浅源地震,在我国的东北和台湾地区及中缅边境和西部境外兴都库什地区也有中源地震和深源地震,这些地震在地表很少形成地震灾害,对社会影响较小,常不被社会所关注。根据国际上震级测定的现状和我国地震活动的实际情况,经专家多次论证以后认为,我国应继续保持自己的震级测定体系为妥。该标准规定了地震震级的测定方法,即使用2个水平方向的资料测定面波震级MS的方法。具体做法如下。
测定浅源地震的面波震级MS,使用基式(SK)中长周期地震仪记录面波质点运动最大速度,计算方法见公式(1)。
| $ {{M}_{\text{S}}}=\text{lg}{{\left(\frac{A}{T} \right)}_{\text{max}}}+1.66\text{lg}\left(\mathit{\Delta } \right)+3.5\ \ \ \ \ {{2}^{\circ }}<\mathit{\Delta }<{{130}^{\circ }} $ | (1) |
式中,A是两水平向面波地动位移的矢量和,T是相应周期,Δ是震中距。
《地震震级的规定》(GB17740—1999)规定用公式(1)测定的震级为地震震级M,称为“地震震级M”,适用于地震部门地震监测、政府部门发布地震预报、防震减灾和新闻媒体报道宣教等。
为了更好地宣传和贯彻国家标准《地震震级的规定》(GB17740—1999),1999年10月出版了《地震震级的规定宣贯教材》(许绍燮,1999)。在该宣贯教材中明确规定“深震和小震对社会的影响不大,它不属于本标准规定的目标范围。在个别特殊情况下(如首都圈等敏感区域发生有感的2级—3级小地震时),需要向社会公布本标准不能测得的地震震级M时,深震可用体波震级mb,小震可用地方性震级ML测定。测定方法可沿用中国地震局现行的《地震台站观测规范》(1990年)的规定。在对社会公布时不再称地震震级M,而应称为相应的体波震级mb或地方性震级ML”。明确指出,对于不能测定面波震级MS的地震,深震可用体波震级mb,小震可用地方性震级ML对外发布,而不能将ML转换MS,或将mb转换MS对外发布震级。
2 ML和MS转换经验公式在实际工作中,曾经根据不同需求给出不同震级之间转换的经验公式。1945年,古登堡(Gutenberg, 1945a, b, c)将地方性震级ML,面波震级MS和体波震级mB简单地用m表示,称为“统一震级”,因为他当时认为这3种震级标度是等价的。但他随后便发现事实并非如此。古登堡与里克特发现,各种震级标度之间存在下列经验关系(Gutenberg and Richter, 1956)。
| $ {{m}_{\text{B}}}=1.7+0.8{{M}_{\text{L}}}-0.01M_{\text{L}}^{2} $ | (2) |
| $ {{m}_{\text{B}}}=0.63{{M}_{\text{S}}}+2.5 $ | (3) |
由式(3)可以看出,mB与MS只有在M大约等于6.5时才是一致的。当M < 6.5时,mB > MS,用mB可以较好地测定地震的震级;当M > 6.5时,mB < MS,用MS可以较好地测定地震的震级。MS标度在M < 6.5时低估了较小的地震震级,但在6.5 < M < 8的震级范围内可以较好地测定出较大地震的震级。
也就是说,不能使用同一震级标度表示所有地震的大小,对于大小不同的地震,最好的办法是使用不同的震级分段表示地震大小。
1966年3月8日河北省邢台地区隆尧县发生6.8级地震,1966年3月22日河北省邢台地区宁晋县发生7.2级地震。2次地震共死亡8 064人,伤38 000人,经济损失10亿元。在周恩来总理直接关怀下,1966年4月,中国科学院地球物理研究所的科技人员仅用时约10天就在北京周边建立了中国第一个遥测地震台网——北京遥测地震台网,该台网由白家疃、平谷、喇叭沟门、下花园、桐柏、周口店、车耳营和马道峪8个地震台组成,采用实线传输单分向短周期地震信号。该台网的建立不仅提高了北京及邻近地区的地震监测能力(监测能力可以达到ML ≥ 2.0)。而且为区域地震台网的建设取得了宝贵经验(中国地震局地球物理研究所,2006)。此后,中国科学院地球物理研究所在红山、宁晋、新河、巨鹿、任县、黄壁庄、康二城、沧州、衡水小侯、临城、河南临县建立固定地震台站,在邢台震区形成内外圈结合的地震台网。1967年3月河间6.3级地震以后,中国科学院地球物理研究所和北京大学先后在河间、文安、武清、宝坻、昌黎凤凰山建立固定地震台站,大部分台站配有短周期地震仪器,部分台站配有中长周期仪器(河北省地震局,2005)。由于台站分布的原因,对于北京遥测地震台网内的监测能力可以达到ML ≥2.0,河北省局部地区监测能力达到ML ≥ 3.0,大部分地区监测能力达到ML ≥ 4.0,加上华北其他省(市)的固定地震台站,能够测定华北地区面波震级MS 4.0以上地震。
1971年郭履灿收集了华北地区能够测定地方性震级ML和面波震级MS的地震观测资料,这些地震的震级范围是MS 4.0—5.7,通过回归分析得到ML和MS的经验公式,为
| $ {{M}_{\text{S}}}=1.13{{M}_{\text{L}}}-1.08 $ | (4) |
该结果于1971年在河北三河召开的全国地震工作会议上通过审定,会议决定该经验公式可以在华北地区使用,但由于当时特定的历史条件,该项研究成果始终未能正式发表,直至1990年,在该年出版的《地震工作手册》(国家地震局震害防御司,1990)中才收录了该结果。根据公式(4)得到ML和MS之间的关系,见表 1。从表 1可以看出,对于ML 4.5—6.0地震,MS均小于ML,并且震级越小,偏差越大。
| 表 1 地方性震级ML与面波震级MS转换表 Tab.1 The transformation of the local magnitude ML and the surface wave magnitude MS |
因此,在使用公式(4)时,一定要注意适用的范围是MS 4.0—5.7,超出了该范围则此公式不一定成立。
为了给出中国地震台网测定的不同震级标度之间的关系,鲍曼和刘瑞丰收集了1983—2004年中国地震台网测定的44 523个地震的地方性震级ML,面波震级MS和MS7,体波震级mB和mb的观测资料,并用一般线性回归方法(SR1和SR2)和正交回归方法(OR)(Carroll et al,1996),分别对不同震级之间的关系进行回归分析与对比,得到的主要结果(Bormann et al,2007)如下:①当M < 4.5时,各种震级标度之间相差不大,使用地方性震级ML可以表示地震的大小;②当4.5 ≤ M < 6.0时,mB > MS,说明MS标度低估了较小地震的震级,因此用mB可以较好地测定较小地震的震级;③当6.0 ≤ M < 8.5时,MS > mB > mb,说明mB与mb标度低估了较大地震的震级,因此用MS可以较好地测定出较大地震的震级;④当M ≥ 8.5时,MS出现饱和现象,不能正确反映大地震的大小。
也就是说,对于我国地震台网测定的地方性震级ML、面波震级MS和MS7、体波震级mB和mb等5种震级,不能使用任何一种震级表示所有地震的大小,对于大小不同的地震,最好的办法是使用不同的震级分段表示地震大小。
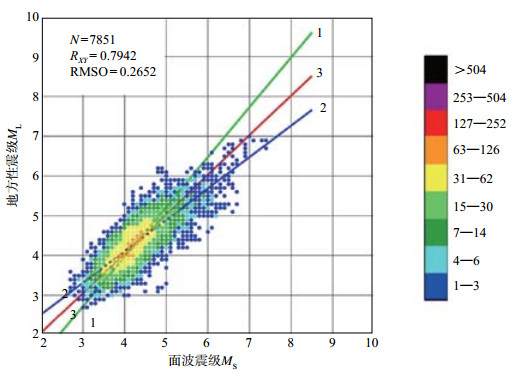
图 1给出ML与MS之间的关系,其中直线3(红色)是采用正交回归方法得到的结果,直线1(绿色)和直线2(蓝色)是使用线性回归得到的结果,彩色色标表示每个点对应的地震数量,例如:红色表示该点有127—252个地震。由正交回归(OR)得到的ML与MS关系直线3界于线性回归(SR1和SR2)得到的直线1与直线2中间。
|
图 1 地方性震级ML与面波震级MS之间的关系(引自Bormann et al,2007) Fig.1 The relationship between local magnitude ML with surface wave magnitude MS (from Bormann et al, 2007) |
从图 1的测定结果来看,可以得出以下结论。
(1)在所选44 523个地震中能够同时测定ML与MS的地震共7 851个,测定台站的震中距均在1 000 km以内。大多数地震震级在3.5≤MS≤ 5.0(黄色和橙色),蓝色的点表示地震数量很少,约1—3个。
(2)ML与MS的实测值离散度大,没有简单的一一对应关系。这是由于测定地方性震级ML使用S波(或Lg波),测定面波震级MS使用面波,S波和面波的周期、幅度差别均较大,计算公式也不同。MS与ML的差值为0的地震数量最多(橙色),绝大多数地震震级差值在-0.5—0.5(黄色),差值最大可达1.7(蓝色)。从图 1也可以看出,并非MS一定小于ML。
(3)地方性震级ML的最大值为7.0,说明对于中国地震台网资料,ML的震级饱和值为7.0,与金森博雄利用全球地震资料得到的结果一致(Kanamori,1983)。
(4)综合分析ML,MS,MS7,mB和mb的正交回归结果(Bormann et al,2007),可以得到一个重要结论:当地震的震级M < 4.5时,各种震级标度之间相差不大,使用地方性震级ML可以表示地震大小。因此,在新国标中规定,对于ML < 4.5的浅源地震,如果不能及时测定地震矩M0,应选择地方性震级ML为对外发布的震级。
汪素云等利用1990—2007年《中国地震年报》中同时给出MS与ML,且震源深度小于70 km的6 577个浅源地震资料,统计回归得到全国和各地震区MS与ML之间的经验关系,得到的结论是:公式(4)与国家地震台网测定的新数据严重偏离,已不适用于新数据,新的震级转换关系接近于MS = ML(汪素云等,2010)。他们认为,对于无法测定MS的低震级地震,可直接使用MS = ML的转换关系(汪素云等, 2009, 2010),这与鲍曼和刘瑞丰得到的结果一致。汪素云等(2009, 2010)得到的结果是另一个强制性国家标准《中国地震动参数区划图》(GB18306—2015)制定的重要依据之一(高孟潭,2015)。
利用中国地震台网的观测资料得到的不同震级标度之间关系的研究成果,也得到了IASPEI震级工作组的认可,并在IASPEI新的震级标准的制定中起到了重要作用(Bormann et al,2009)。
3 地震速报震级的确定《地震震级的规定》(GB17740—2017)实施以前,在地震速报时国家地震台网将面波震级MS(震级M)作为发布震级,省级地震台网测定地方性震级ML,利用表 2将ML转换成面波震级MS后对外发布。而对于5.0级以上地震,一些省级地震台网也测定面波震级MS,用面波震级对外发布。
| 表 2 在速报时使用的地方性震级ML与面波震级MS转换表 Tab.2 The transformation of the local magnitude ML and the surface wave magnitude MS in earthquake parameters fast report |
从表 1和表 2可以看出,表 2所涉及的震级范围明显变大,地方性震级ML从4.5降低到1.0。而随着震级的降低,ML与MS之间的偏差也在逐渐增大,当ML为4.0时MS为3.5,当ML为3.0时MS为2.3,当ML为2.0时MS为1.2,当ML为1.0时MS为0.1。因此,表 2给出的ML与MS转换表明显超出公式(2)的适用范围,主要存在以下问题。
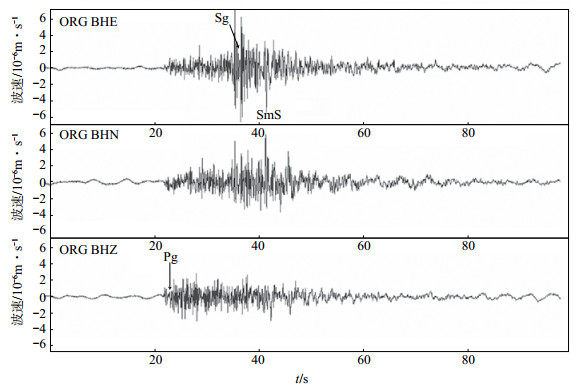
(1)小地震激发不出面波,无法测定面波震级MS。根据云南地震台网(杨晶琼等,2016)和四川地震台网(黄春梅等,2018)的实际地震记录,对于4.5级以上地震,当震中距大于250 km时能够记录到面波。如图 2是昆明地震台记录的2002年8月5日云南元谋ML 3.2地震,可以在宽频带记录上清楚识别Pg,Sg等震相,但没有面波,这样的地震是不能测定面波震级MS的。
|
图 2 昆明地震台记录到的云南元谋ML 3.2地震 Fig.2 Waveform of Yuanmou ML 3.2 earthquake in Yunnan recorded at Kunming Seismic Station |
对于4.5级以下地震,如果不能测定面波震级MS,将ML按表 2转换MS以后发布震级,实际上该面波震级MS是不存在的,等于人为压低了震级,导致震级越小、偏差越大。
(2)违反强制性国家标准《地震震级的规定》震级发布规则。无论是原国标,还是新国标,在震级发布规则上都是一致的,大地震对外发布面波震级MS、小震发布方性震级ML,深震发布体波震级mb,只不过是在新国标中给出了量化指标,把相关内容用强制性条款规定下来,而原国标在宣贯教材中给出了明确说明。
(3)违反了在地震监测中测定的震级之间不应相互换算的基本规则。地震监测注重观测量的实测值,地震台网实测的地方性震级ML,体波震级mb,面波震级ΜS,矩震级MW之间一律不允许相互转换。因此,在台网的观测报告和数据库中给出的均为实测震级。
4 社会需求随着我国社会经济的不断发展,城市化进程不断加快,高楼、大桥越来越多,各级政府和社会公众对地震速报的要求不断提高,对于有感地震更加关注。对于ML 4.5以下地震,如果将测定的地方性震级ML转换成面波震级MS,会使震级明显降低,致使一些有感地震未纳入正式速报地震范围,从而导致某些相关事件发生后,地震部门往往因社会公众质疑“地震漏报”而陷入舆论被动。例如在2016年3月中下旬山西运城震群中,15天内发生3.0级以下有感地震多达9次,山西地震台网测定的地方性震级ML在3.0—3.5,利用表 2转换成面波震级MS以后震级在2.3—2.9。由于转换以后的震级小于3.0,根据中国地震局颁发的《地震速报技术管理规定》,无论是山西地震台网,还是国家地震台网均未发布这9次有感地震的速报信息,从而造成较大社会影响。
自2006年以来,浙江省温州市珊溪水库地区发生多次地震活动,仅2006年2月—10月浙江地震台网和珊溪水库地震台网共记录ML 1.0以上地震1 137次,绝大多数是ML 2.0以下地震,最大为ML 4.6地震(邹振轩等,2010)。将实际测定的ML转换成MS后,满足地震速报条件的地震很少,无法满足浙江省政府和温州市政府的要求。
在华东地区,上海市是我国首批沿海开放城市,是我国经济、金融、贸易和科技创新中心,超高层建筑密布,人口众多。若在上海市区发生ML 1.5以上地震,高层居住人群有感,地震部门必须将这样的地震信息及时向社会发布,以免引起社会恐慌。如果将实际测定的ML转换成MS,从表 2可知,1.5级变成0.6级,转换以后的震级明显变小,达不到发布标准,将不可避免地出现一些不利信息。
新国标于2018年2月1日开始实施,在2月6日中国台湾花莲6.5级地震、2月12日河北永清4.3级地震、2月14日河北张北3.2级地震和2月17日墨西哥7.1级地震的速报中取得较好效果。尤其是在河北永清4.3级地震和张北3.2级地震的速报中,充分发挥了新国标的优势。2月12日河北永清4.3级地震发生后,北京市、天津市和廊坊市普遍有感,当时测定的地方性震级为ML 4.8,台站记录的Lg波周期达到3—5 s,明显高于测定ML所需的地震波优势周期0.8 s,导致测定的ML震级偏高,随后测定的宽频带面波震级MS(BB)为4.3,由此对外发布的地震震级M为4.3,后来中国地震局地震预测研究所测定的矩震级MW为4.3,此次地震的速报取得了良好的科学效益和社会效益;2月14日河北张北3.2级地震发生后,张北县和尚义县局部有感,河北地震台网测定的地方性震级为ML 3.2,对外发布的地震震级M为3.2。如果采用原地震速报管理规定,将ML 3.2按表 2转换为MS 2.5,未达到3.0级速报要求,就可以不发布该地震参数。
新国标的实施,避免了地震部门因社会公众质疑“地震漏报”而陷入的舆论被动。以上2次河北地震发生后,引起河北省政府高度重视,省政府主要领导到张北了解震情。有人提出,如果按以前的地震速报方式可以不发布张北地震参数,就不会引起河北省政府和社会的关注。我们认为这是不可取的,对于有感地震,如果漏报将会引起社会混乱,使地震部门处于被动状态。河北省政府除了关注地震多大,更重要的是关注震情的发展趋势,近期是否会发生更大地震。因此,我们认为,无论是国家地震台网,还是省级地震台网,都应向政府和公众提供科学、客观的地震参数,及时、准确地判断并给出震情发展趋势,是政府和公众所关切的重要信息。
5 结语新国标充分体现了震级的多样性和复杂性,规定了地方性震级ML,短周期体波震级mb,宽频带体波震级mB(BB),面波震级MS,宽频带面波震级MS(BB)和矩震级MW等6种震级的测定方法,测定的震级之间不应相互换算,并将矩震级MW作为地震台网重点测定的震级和对外发布的首选震级。
为确保在第一时间将地震参数向社会快速发布,对于不能及时测定矩震级的地震,新国标规定规定:对于ML < 4.5的浅源地震,应选择地方性震级ML为对外发布震级;对于ML ≥4.5的浅源地震,应选择宽频带面波震级MS(BB)为对外发布震级;对于中深源地震,选择体波震级为对外发布震级,不再使用依赖于统计经验的震级转换,而是根据地震特征,从测定的震级标度中选择最能反映地震实际情况的结果优先发布。既保全测定震级的科学属性,也兼顾社会的实际需求。
| 陈运泰, 吴忠良, 王培德, 许力生, 李鸿吉, 牟其铎. 数字地震学[M]. 北京: 地震出版社, 2000: 1-10. | |
| 高孟潭. 中国地震动参数区划图(GB18306-2015)宣贯教材[M]. 北京: 中国标准出版社, 2015, 30-35. | |
| 黄春梅, 苏金蓉, 唐淋, 魏娅玲, 吴朋, 王宇航. 新震级国家标准在四川台网的应用——宽频带面波震级[J]. 华北地震科学, 2018, 36(1): 25-30. | |
| 汪素云, 俞言祥. 震级转换关系及其对地震活动性参数的影响研究[J]. 震灾防御技术, 2009, 4(2): 141-149. DOI:10.11899/zzfy20090202 | |
| 汪素云, 王健, 余言祥, 吴清, 高阿甲, 高孟潭. 基于中国地震台网观测报告的ML和MS经验关系[J]. 中国地震, 2010, 26(1): 14-22. | |
| 许绍燮. 地震震级的规定(GB17740-1999)宣贯教材[M]. 北京: 中国标准出版社, 1999, 6-7. | |
| 许绍燮, 陆远忠, 郭履灿, 陈培善. 地震震级的规定(GB17740-1999)[M]. 北京: 中国标准出版社, 1999, 1-2. | |
| 杨晶琼, 杨周胜, 蔡明军, 许亚吉, 梁勇. IASPEI宽频带面波震级与传统面波震级的对比[J]. 地震研究, 2016, 39(2): 303-307. | |
| 邹振轩, 李金龙, 俞铁宏, 王政. 温州珊溪水库地震S波分裂研究[J]. 地震学报, 2010, 32(4): 423-432. | |
| 河北省地震局. 河北省地震监测志[M]. 北京: 地震出版社, 2005, 1-50. | |
| 国家地震局震害防御司. 地震工作手册[M]. 北京: 地震出版社, 1990, 128-129. | |
| 中国地震局地球物理研究所. 中国地震局地球物理研究所地震监测志[M]. 北京: 地震出版社, 2006, 1-4. | |
| Bormann P, Liu R F, Ren K X, Gutdeutsch R, Kaiser D, Castellaro S and Chinese National Network Magnitudes. Their Relation to NEIC Magnitudes, and Recommendations for New IASPEI Magnitude Standards[J]. Bull Seismol Soc Am, 2007, 97(1B): 114-127. DOI:10.1785/0120060078 | |
| Bormann P, Liu R F, Xu Z G, Ren K X, Zhang L W, Wendt S. First Application of the New IASPEI Teleseismic Magnitude Standards to Data of the China National Seismographic Network[J]. Bull Seismol Soc Am, 2009, 99(3): 1 868-1 891. DOI:10.1785/0120080010 | |
| Carroll R I, Ruppert D. The use and misuse of orthogonal regression in linear errors-in-variables models[J]. The American Statistician, 1996, 50(1): 1-6. | |
| Gutenberg B. Amplitudes of surface waves and magnitudes of shallow earthquakes[J]. Bull Seismol Soc Am, 1945a, 35(1): 3-12. | |
| Gutenberg B. Amplitudes of P, PP and S and magnitude of shallow earthquakes[J]. Bull Seismol Soc Am, 1945b, 35(2): 57-69. | |
| Gutenberg B. Magnitude determination for deep-focus earthquakes[J]. Bull Seismol Soc Am, 1945c, 35(3): 117-130. | |
| Gutenberg B, Richter C F. Magnitude and energy of earthquakes[J]. Annali di Geofisica, 1956, 9(1): 1-15. | |
| Hanks T C, Kanamori H. A moment magnitude Scale[J]. J Geophy Res, 1979, 84(B5): 2 348-2 350. DOI:10.1029/JB084iB05p02348 | |
| Kanamori H. The energy release in great earthquakes[J]. J Geophys Res, 1977, 82: 2 981-2 987. DOI:10.1029/JB082i020p02981 | |
| Kanamori H. Magnitude scale and quantification of earthquakes[J]. Tectonophysics, 1983, 93: 185-199. DOI:10.1016/0040-1951(83)90273-1 | |
| Purcaru G, Berckhemer H. A magnitude scale for very large earthquakes[J]. Tectonophysics, 1978, 49(3/4): 189-198. | |
| USGS. New USGS earthquake magnitude policy[R]. MCEER Information Service News, 2002: 1-3. |
 2018, Vol. 39
2018, Vol. 39