地应力变化是地震发生的重要原因(邱泽华,2010),地壳形变会产生应力集中并引发地震,所以地震与地壳形变密切相关。钻孔应变观测是研究地壳变形和地应力场变化的一种重要手段。1968年9月,美国卡奈基研究所的Sacks和德克萨斯大学的Evertson研制出世界上第一台钻孔(体)应变仪(邱泽华等,2010)。1966年邢台地震后,中国采用电感元件在钻孔中观测地应力变化,进行地震预报研究(国家地震局地震地质大队,1976)。
自1984年新疆维吾尔自治区地震局建立钻孔应变观测网以来,利用观测资料对新疆及附近区域几次强震做出较好预报,连续7年获中国地震局年度预报评比前三名,并获1993—1997年中国地震局防震减灾优秀成果二等奖(蒋靖祥等,2000)。钻孔应变观测资料多次在新疆及邻区强震前记录到异常变化(蒋靖祥等, 2000, 2002, 2003, 2004):1993年2月3日和静5.7级地震、10月2日若羌6.6级地震、1996年11月19日喀喇昆仑山口7.1级地震、1997年11月8日西藏玛尼7.5级地震、2001年11月14日新青交界8.1级地震等,其中1993年2月3日和静5.7级地震前,记录到趋势、短期、临震异常,并据此于震前做出趋势、短期、临震预报。
自电感法钻孔应力仪诞生以来,连续地应变观测是地震预报研究从“经验预报”转向物理预报的依据,观测资料可靠性问题需要解决。四分量钻孔应变仪具有独有的可以自行检验观测资料的可靠性(邱泽华等,2009)。1977年由苏恺之(2003)提出四分量概念以来,自检方法得到普遍应用。所谓自检,是将4个元件的读数带入自检公式,根据互检条件(相关系数是否接近于1)快速得出可靠性结论。随着工作的深入,对数据的可靠性要求逐步提高,有人提出实地相对标定(计算各个元件校正系数),并可进一步采用理论固体潮进行实地绝对标定(计算探头校正系数)(邱泽华等,2005)。本文采用数据自检、潮汐因子内精度计算、与同一时段相邻区域陆态网络形变观测资料进行对比等方法,对库尔勒地震台的巴伦台、库米什、小泉沟子台3套RZB-Ⅱ钻孔应变仪观测资料的可靠性进行论证。
1 台站简介库尔勒地震台的巴伦台、库米什、小泉沟3个钻孔应变观测子台属于天山中段地震前兆台网建设项目,是中国地震局地壳应力研究所援疆项目。2014年11月完成库米什、巴仑台钻孔应变仪安装,2015年完成小泉沟钻孔应变仪安装,2016年9月1日至11月30日进入试运行阶段。3个台站地质构造及观测仪器元件参数见表 1,其中巴伦台钻孔最深,库米什钻孔为干孔。
| 表 1 库米什、巴伦台、小泉沟应变台站参数 Tab.1 The basic situation of the strain stations |
选取2016年12月至2017年5月应变观测整点值数据,计算潮汐因子内精度、自检内精度及面应变相关系数,检验观测资料的可靠性。
2.1 潮汐因子“内精度”(中误差)一般根据潮汐因子内精度(中误差)进行体应变观测资料质量评价,所以可将潮汐因子内精度作为分量式钻孔应变观测资料可靠性评价的一项重要指标(唐磊等,2010)。钻孔应变观测数据潮汐因子内精度指标是,按Venedikov调和分析方法,对1月长度的应变观测数据进行调和分析,以M2波振幅因子的相对中误差指标来评定应变观测数据质量,要求Ⅰ类应变台站观测数据相对中误差指标<0.05(吴云等,2008)。按照4个分量分别计算3个子台应变观测数据的潮汐因子内精度,2016年12月—2017年5月钻孔应变观测数据潮汐因子内精度统计结果见表 2。
| 表 2 四分量钻孔应变观测数据潮汐因子内精度(中误差) Tab.2 Internal accuracy (mean square error) of tide factors in four component borehole strain observation data |
(1)巴伦台潮汐因子内精度最好,库米什次之,小泉沟较差。潮汐因子内精度主要取决于观测仪器质量,也与应变台站所处地质环境有关,钻孔处基岩越完整,干扰越少,潮汐因子内精度越高。钻孔柱状图显示,3个台基岩较完整,质地坚硬、结构密实。
(2)巴伦台、库米什潮汐因子内精度均达到优等。2017年1月17日—23日、2月12日—13日、2月18日—19日、2月22日—24日,小泉沟子台四分量出现幅度较大的压缩—拉张异常变化和丛集高频信号,尤其是EW、NW向较为严重,导致1月、2月的潮汐因子内精度较低;3—5月潮汐因子内精度达到优等。各分量潮汐因子内精度结果显示,巴伦台、库米什表现出较为一致的特征,即四分量中EW分量潮汐因子内精度稍低。小泉沟与其他2个台略为不同的是,四分量中NW分量潮汐因子内精度稍低。除小泉沟2017年1—2月四分量出现的异常变化导致潮汐因子内精度较低外,3个台应变观测资料潮汐因子内精度均达到优等,表明3个台应变观测数据可靠。
2.2 自检内精度 2.2.1 相对标定计算潮汐因子中误差大小还不足以充分论证钻孔应变观测资料的可靠性,例如:当某个测量元件格值有明显系统偏差时,不会在中误差数值里有所显现。因此,需要对4个元件之间格值的一致性(即是否有系统偏差的不一致)给予检查和纠正,称之为相对标定。邱泽华等(2005, 2009)提出钻孔四分量应变观测实地标定方法,根据一定假设条件对元件观测值进行校正。令
| $ {S_i} = {k_i}{R_{\rm{i}}}\;\quad \quad \quad \quad \left( {i = 1,2,3,4} \right) $ | (1) |
其中,Si为各元件的观测值,Ri为需要矫正的观测值,根据四分量钻孔应变特性,则
| $ {S_1} + {S_3} = {S_2} + {S_4} $ | (2) |
将实际观测值代入式(2),设定任意一个ki = 1,反演得到其他ki。分别给定不同ki = 1,得到4组ki(i = 1,2,3,4),取平均值作为最终反演结果。ki均应在1附近取值,特别是探头与围岩的耦合处于理想状况时,ki = 1。ki的这种反演为实地相对标定,为相对校正系数。用Si(i = 1,2,3,4)替代Ri(i = 1,2,3,4),应该更接近真实孔径的相对变化。ki越近于1,表明仪器制作和下井安装质量越好,观测数据质量越高。唐磊(2015)在相对标定基础上,提出自检内精度,对于理想情形,相对校正系数均应等于1。由4个元件的标定系数求出均值和偏差,仿照潮汐因子内精度概念,定义
| $ \alpha = \frac{S}{R} $ | (3) |
其中,α为相对标定自检精度;S为偏差,是相对于4个元件校正系数的均值来计算的;R为4个元件相对校正系数均值的绝对值。为了适合k值的设定,计算偏差时改用4个相对校正系数相对于1的偏差。
| $ S = \sqrt {\frac{{\sum {{{\left( {{k_i} - 1} \right)}^2}} }}{4}}\quad \quad \quad \quad \;\left( {i = 1,2,3,4} \right) $ | (4) |
利用该指标对观测数据进行质量评价时,自检内精度α越小,观测数据质量越高。
2.2.2 面应变相关系数根据钻孔四分量观测的自洽方程,可以得到面应变1(S1 + S3)、面应变2(S2 + S4),通过原始数据得到一组面应变。将原始数据进行相对标定后可以得到一组面应变,每组面应变均可计算1个相关系数,即
| $ r = \frac{{\sum {{S_{13}}{S_{24}} - \frac{{\sum {{S_{13}}\sum {{S_{24}}} } }}{N}} }}{{\sqrt {\left( {\sum {S_{13}^2 - \frac{{{{\left( {\sum {{S_{13}}} } \right)}^2}}}{N}} } \right)\left( {\sum {S_{24}^2} - \frac{{{{\left( {\sum {{S_{24}}} } \right)}^2}}}{N}} \right)} }} $ | (5) |
其中,r表示相关系数;S13表示“S1 + S3”,即面应变1;S24表示“S1 + S3”,即面应变2;N表示数据数。利用该指标对观测数据进行质量评价时,2组面应变相关系数越接近1,观测数据质量越高。
根据钻孔四分量观测特点,潮汐因子内精度不能作为观测数据质量评价的唯一指标,而相对标定系数指标中,4个元件的标定系数可能均接近1,地震台站较多时,无法判定哪个台站观测质量较高,因此,中国地震局钻孔应变学科组2009年提出相对标定自检内精度指标(董雪梅等,2014),自检内精度<0.2为优等精度(唐磊等,2010)。从侧面表明仪器质量和观测资料的可靠性,尽管如此,本文仍正面做进一步的可靠性论证。
选取3个台2016年12月至2017年5月应变观测整点值数据,根据自检内精度和面应变相关系数定义,计算结果见表 3。
| 表 3 四分量钻孔应变观测数据质量评价结果 Tab.3 Quality evaluation results of four component borehole strain observation data |
(1)巴伦台自检内精度较高,库米什次之,小泉沟较差。与潮汐因子内精度排序一致。巴伦台各月自检内精度均达到优等;除2017年4月外,库米什其余月份自检内精度均达到优等;小泉沟2017年1—2月,四分量出现幅度较大的压缩—拉张异常变化和丛集高频信号,导致1月、2月的自检内精度较低,3月4日现场异常核实人为干扰造成自检内精度较低,4—5月自检内精度达到优等。实际观测中,数据曲线可能受到干扰而发生突变,各元件的观测值就可能不符合自检方程。
文中3套钻孔应变仪器的校正系数均在1上下,表明仪器出厂质量较好,安装过程较好,观测数据可靠。
(2)巴伦台元件相对校正系数ki均在1附近,表明观测数据质量较高;库米什2017年4月元件相对校正系数ki偏低,其余月份基本在1附近,说明2017年4月观测数据质量不高;小泉沟元件相对校正系数k4普遍较低,说明NW向观测数据质量不高,与潮汐因子内精度计算结果一致。分析认为,可能是井下探头中的4#元件灵敏度发生了不一致变化,探头安装过程中,由元件所处位置的温度等因素影响而产生。
(3)巴伦台、库米什原始数据和相对标定后的面应变相关系数差别不大,且相关系数普遍达到0.99,说明巴伦台观测数据质量较高;小泉沟原始数据面应变相关系数较其他2个台低,且2017年2月、3月相对标定后,较原始数据面应变相关系数有较大幅度地提升,尤其是2017年3月,原始数据面应变相关系数为0.825 6,相对标定后达0.982 3。利用钻孔应变观测数据进行地震科学研究,必须对观测数据进行相对标定及自检分析。
2.2.3 相关系数影响因素钻孔基岩性质和岩石完整性对观测数据内精度影响较大。李进武等(2014)对18个应变台观测数据进行相对标定、绝对标定、反演,并进行应变换算,采用球状径向不均匀弹性地球模型计算理论应变固体潮,并运用调和分析方法,得到面应变固体潮M2波潮汐振幅因子,分析潮汐因子变化特征及影响因素,发现围岩性质对潮汐因子影响明显。受条件限制,库尔勒地震台3个应变观测点无钻孔基岩岩性力学参数岩样的杨氏模量等弹性参数,后续研究可以考虑测试仪器安装点的岩性,有条件时可以在岩性相同的局部区域多布设一些仪器,便于对比分析、互相验证。
区域构造运动和地壳介质的各向异性也会对观测数据精度产生较大影响。鲍子文等(2017)通过对天山构造带上39个地震台站的地壳剪切波分裂进行分析,认为天山构造带及邻区的地壳介质各向异性具有明显的分区性,各向异性参数与地震台站附近的局部构造、地壳介质变形和应力分布有重要关系。天山构造带主要区域剪切波偏振优势方向大致平行于构造带走向。
由表 1可以得到3个应变台元件方位平面图,见图 1。在分量应变仪器安装过程中,1#元件由电子罗盘确定方位角后下井,沿顺时针依次相隔45°分别布置2#、3#和4#元件。

|
图 1 库尔勒台应变观测元件方位角 Fig.1 Azimuths of Strain observation elements at Korla Seismic Station |
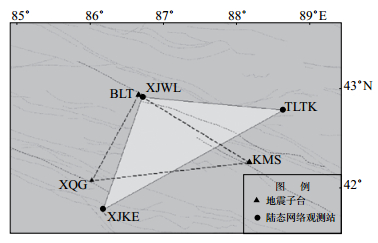
巴伦台、库米什、小泉沟内子台应变观测EW、EW、NW分量精度稍低,结合图 1,3个子台潮汐因子内精度稍低的真实方向分别应为NNE、NW、NW;相对标定自检内精度结果显示,小泉沟子台4#元件相对校正系数k4普遍偏低,其所表征的方向为NW。结合天山构造带和3个应变台站所处断裂(图 2),初步分析内精度稍低的原因。
|
图 2 天山构造带构造单元及应变台站分布 Fig.2 Tectonic units and distribution of stations in the Tianshan tectonic belt |
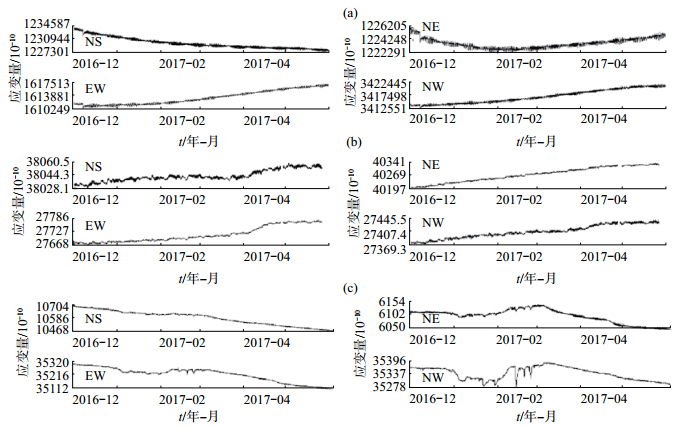
|
图 3 库尔勒台分量钻孔应变数据 (a)巴伦台子台;(b)库米什子台;(c)小泉沟子台 Fig.3 Borehole strain data of Korla Seismic Station |
由图 2可见,3个子台所处断裂均呈NW向展布,其中库米什、小泉沟子台内精度稍低方向与天山构造带和台站所处断裂展布呈现出较好的一致性,巴伦台子台钻孔所处的乌拉斯台断裂倾向NNE,倾角60°—80°,观测数据内精度稍低的方向为NNE,与断裂倾向表现出较好的一致性。对库米什、小泉沟子台而言,NW向断裂带的存在,似乎影响了接近该方向元件应变的接收,所以此元件观测数据质量略有降低;巴伦台子台所处断裂虽整体呈NW向展布,但断裂倾向NNE,认为接近该方向的元件可更直接地接收该方向上的应变,因此导致观测质量略低。
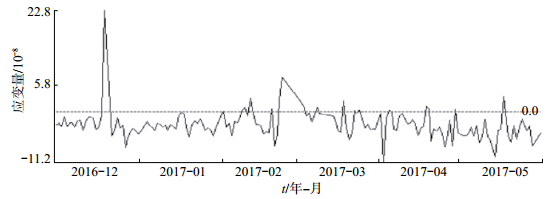
3 形变观测资料对比论证3个子台应变观测资料潮汐因子内精度、自检内精度、面应变相关系数均达到优等,反映了库尔勒地震台3套四分量钻孔应变观测资料的可靠性。选取2016年12月—2017年5月3个子台邻近区域陆态网络观测资料进行对比,即分析3个钻孔应变台所围区域呈压缩还是拉张变化,是否与同期临近区域陆态网络观测结果一致,进一步论证四分量钻孔应变观测资料的可靠性。结果显示:对于四分量钻孔应变观测资料,巴伦台子台NS向呈压缩变化,其余3个分量呈拉张变化,库米什子台4个分量均呈拉张变化,小泉沟4个分量均呈压缩变化(图 3),3个台所围区域显示NS向受挤压,呈压缩变化;由陆态网络观测资料可知,与3个子台所围区域临近的库尔勒GNSS站(XJKE)、乌拉斯台GNSS站(XJWL)和托克逊CORS站(TLTK)组成一个块体。为计算确定该块体的压缩—拉张性质,通过数据解算得到该块体面膨胀结果(图 4)和空间分布(图 2)。从图 4可见,库尔勒、乌拉斯台、托克逊所围块体(图 2中浅灰色填充三角形)面膨胀结果整体为负数,表明该块体受挤压呈压缩变化。
|
图 4 陆态网络数据面膨胀解算结果 Fig.4 Surface expansion calculation results of GNSS data |
图 2显示,巴伦台、库米什、小泉沟3个四分量钻孔应变台所围区域(虚线三角形)与陆态网络观测站点所围区域(填充三角形)部分重叠,其中巴伦台和乌拉斯台相距较近,共同显示出受挤压的压缩变化,小泉沟子台也呈压缩变化。此结果较好地验证了天山地区构造活动特征,即天山NS向的挤压缩短呈现不均匀分布特征,且主要集中在南北两侧盆地山体过渡地带(牛之俊等,2007),天山南北两侧及邻近地区以压应变为主(王晓强等,2007),最大主压应力方向在天山地区略有局部差异(高国英等,2010)。天山NS向的挤压使得位于NS向的巴伦台、小泉沟子台成为直接受力挤压部位,库米什子台则在与挤压力垂直的方向上,根据弹性力学理论,认为库米什子台应该呈现出拉张变形的特点。3个子台的应变观测资料呈现出与区域构造活动一致的变化,可以认为真实反映了台站所在区域的应变变化特征,即钻孔应变观测资料是可靠的。
4 结束语综上所述,3套四分量钻孔应变仪产出数据的自检效果,即相关系数可达0.99或0.999以上,可以肯定仪器的工作质量和产出数据的可靠性,慎重起见,本文做了较为全面的多视角的审视,所得结论一致。
利用四分量钻孔应变观测资料的潮汐因子内精度、相对标定自检内精度、面应变相关系数等判定观测资料可靠性,并采用同时段相近区域陆态网络形变资料进行对比分析,论证巴伦台、库米什、小泉沟子台四分量钻孔应变观测资料的可靠性。3个应变台站同处天山构造带上,4个分量观测数据内精度存在差异,分析认为内精度稍低分向与钻孔所处断裂展布方向呈现出较好的一致性,表明在主压应力方向上强烈受力变形。但由于地壳介质的各向异性,巴伦台与其他2个台站呈现不同特点。元件相对校正系数、自检内精度和面应变相关系数等观测数据质量评价指标根据四分量钻孔应变观测特点提出的,能够客观评价钻孔四分量应变观测资料的质量。利用四分量钻孔应变数据进行应变换算,有必要对观测数据进行相对标定处理和自检分析。
论文撰写得到中国地震局地壳应力研究所苏恺之研究员的悉心指导,在此表示诚挚谢意。| 鲍子文, 高原. 天山构造带及邻区地壳各向异性[J]. 地球物理学报, 2017, 60(4): 1359-1375. DOI:10.6038/cjg20170411 | |
| 董雪梅, 伍永秀, 徐建明, 等. 四川前兆钻孔应变观测数据质量影响因素分析[J]. 四川地震, 2014, 4: 11-14. | |
| 国家地震局地震地质大队. 与中国科学院兰州地球所的几位同志谈地震预报(1966年10月)[C]//李四光同志有关地震工作谈话选辑. 1976: 5-6. | |
| 高国英, 聂晓红, 龙海英. 2003-2008年新疆区域构造应力场特征探讨[J]. 地震地质, 2010, 32(2): 70-79. | |
| 蒋靖祥, 尹光华, 哈斯高娃. 钻孔应变仪在地震前的记录及地震预测[J]. 地震研究, 2000, 23(4): 410-417. | |
| 蒋靖祥, 尹光华, 许风柱. 新疆和静5.7级地震前钻孔应变异常及预报[J]. 四川地震, 2002, 3: 21-26. DOI:10.3969/j.issn.1001-8115.2002.03.004 | |
| 蒋靖祥, 王在华, 李川, 等. 新疆钻孔应变异常与强震活动[J]. 内陆地震, 2003, 17(2): 126-133. | |
| 蒋靖祥, 王在华, 唐小勇, 等. 新疆地区钻孔应变观测及地震前兆研究[C]//地壳构造与地壳应力文集. 2004, (17): 45-56. | |
| 李进武, 邱泽华. 钻孔应变仪观测的面应变潮汐因子初步分析[J]. 地球物理学进展, 2014, 29(5): 2013-2018. DOI:10.6038/pg20140504 | |
| 牛之俊, 游新兆, 杨少敏. 利用GPS分析天山现今地壳形变特征[J]. 大地测量与地球动力学, 2007, 27(2): 1-9. | |
| 邱泽华, 石耀霖. 国外钻孔应变观测的发展现状[J]. 地震学报, 2004, 26(2): 162-168. | |
| 邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 2005, 25(1): 118-122. | |
| 邱泽华, 石耀霖, 欧阳祖熙. 四分量钻孔观测的实地绝对标定[J]. 地震, 2005, 25(3): 27-34. | |
| 邱泽华, 阚宝祥, 唐磊. 四分量钻孔应变观测资料的换算和使用[J]. 地震, 2009, 29(4): 410-417. | |
| 邱泽华. 中国分量钻孔地应力-应变观测发展重要事件回顾[J]. 大地测量与地球动力学, 2010, 30(5): 42-47. | |
| 苏恺之. 地应力相对测量方法[M]. 钻孔地应变观测新进展.北京: 地震出版社, 2003, 252-260. | |
| 唐磊, 邱泽华, 宋茉. 钻孔四分量应变观测自检内精度分析[J]. 大地测量与地球动力学, 2010, 30(2): 36-39. | |
| 唐磊, 吕品姬. 钻孔四分量应变观测数据不同时间尺度的自检分析[J]. 大地测量与地球动力学, 2015, 35(3): 525-528. | |
| 王晓强, 李杰, ZubovichA, 等. 利用GPS形变资料研究天山及邻近地区地壳水平位移与应变特征[J]. 地震学报, 2007, 29(1): 31-37. | |
| 吴云. 地形变测量[M]. 北京: 地震出版社, 2008, 312-313. |
 2018, Vol. 39
2018, Vol. 39