2. 中国北京 102628 北京港震仪器设备有限公司
2. Beijing Gangzhen Instrument and Equipment Corporation, Ltd., Beijing Municipality 102628, China
地震计传递函数是描述地震计输入、输出关系的表达式,是地震观测、地震学研究的第一手关键资料。早期机械地震计可以通过测试地震计自振周期和阻尼获得二阶传递函数。电子反馈型地震计的传递函数受电子线路影响,由于机械部分和电子器件性能离散性,通过正向推导获得准确的传递函数存在困难。地震计生产厂家一般采用实际测试方法确定地震计传递函数,主要采用振动台方法、电标定方法等。
振动台方法是对地震计整体施加振动,与地震计工作模式一致,是一种客观标定方式。目前该方法主要用于地震计幅频特性测试,由于缺少同步振动台记录波形,不能测定相频特性。
电标定方法给地震计磁缸内的标定线圈输入一个电流(Peterson J et al,1980;王广福,1986;Rodgers P W et al,1995;李海亮,2000;Bormann P,2002),产生驱动力驱动地震计摆锤运动以等效成地面运动。目前电标定可以远程控制,标定时地震计放置在稳定地面,保持环境安静,干扰较小,可以更加准确地测定地震计响应。电标定方法根据信号不同主要可分为阶跃标定、伪随机码标定和正弦波标定。
阶跃标定信号自身频谱特性决定其低频信号强,高频成分随频率的平方衰减,有利于测定地震计低频特性。事实上,基于地震计阶跃标定响应特性推导的时域波形方程和响应频谱公式,准确给出了地震计自振周期和阻尼系数的关系。基于此,阶跃标定主要用于确定地震计低频特性。
伪随机码标定方法(Berg E et al,1976;Berger J et al,1979;林湛等,2015)是向地震计发送精心设计的伪随机二进制码信号,通过处理地震计响应来获得地震计幅频特性。本质上二进制码信号是一系列不同宽度的阶跃信号组合,其能量在频率分布上具有不均匀性,且高频信号强度不足,通过谱除法获得频率特性有较大波动,信噪比变化较大,经过拟合也可求得传递函数,置信程度有一定不足。
在取得地震计的频率特性和相位特性后,采用拟合方法得到地震计传递函数,是一种通行方法(Bolduc P M et al,1972;王广福,1986;Kim W Y et al,1996)。正弦波标定使用广泛,不同频率可以设定相应激励电流,保证在测试点具有足够信噪比的信号用于确定频率特性。传统正弦标定方法限于测定地震计的幅频特性,而不测定相频特性。本文提出改进的技术措施,同时获取幅频频特性和相频特性,并利用阶跃标定特点,准确测定地震计自振周期和阻尼,确定地震计低频特性;在拟合地震计传递函数时,根据地震计频率特性的特点构造传递函数的形式,并约束低频传递函数参数,保证结果的合理性和可靠性。
1 测试原理与方法 1.1 反馈式地震计传递函数表述任意一个系统的传递函数均可表示一个滤波器,其形式是2个多项式的商。本文定义反馈式地震计的传递函数为在频域经过归一化的地震计响应,由2个部分组成,其中低频部分取决于等效机械摆的自振角频率和阻尼系数,称为低频传递函数,记为H0(s);另一部分主要影响地震计的高频特性,称为高频传递函数,记为H1(s)。地震计的总体频率特性、低频和高频特性可分别用式(1)、(2)、(3)来描述。
| $ H\left(s \right) = {H_0}\left(s \right){H_1}\left(s \right) $ | (1) |
| $ {H_0}\left(s \right) = \frac{{{s^2}}}{{{s^2} + 2{D_0}{\omega _0}s + \omega _0^2}} $ | (2) |
| $ {H_1}\left(s \right) = \frac{{{b_m}{s^m} + {b_{m - 1}}{s^{m - 1}} + \cdots + {b_1}s + {b_0}}}{{{a_n}{s^n} + {a_{n - 1}}{s^{n - 1}} + \cdots + {a_1}s + {a_0}}} $ | (3) |
其中:H0(s)为等效固有周期机械摆的二阶传递函数,即低频传递函数,s为Laplace算子,D0为等效机械摆的阻尼系数,ω0为等效机械摆自振周期,(an,an-1,...,a1,a0)、(bm,bm-1,...,b1,b0)分别为其分子分母多项式的系数。式(2)中的H0(s)由阶跃标定获得的自振周期和阻尼系数确定。式(3)中的H1(s)描述地震计传递函数的高频段特性,取决于地震计的电路特性。(an,an-1,...,a1,a0)、(bm,bm-1,...,b1,b0)系数用最优化拟合确定,是本文研究重点。
1.2 地震计自振周期与阻尼系数确定阶跃标定是确定地震计自振周期和阻尼的有效可靠的方式(李海亮,2000)。地震计阶跃响应的记录波形在时间域和频率域内可分别由式(4)、(5)描述。
| $ r\left(t \right) = \frac{K}{{{\omega _0}\sqrt {1 - D_0^2} }}{e^{ - {D_0}{\omega _0}t}}\sin \left({{\omega _0}\sqrt {1 - D_0^2} t} \right) $ | (4) |
| $ {R_0}\left(s \right) = K{H_0}\left(s \right) = \frac{K}{{{s^2} + 2{\omega _0}{D_0}s + \omega _0^2}} $ | (5) |
阶跃响应由K、ω0、D0参数唯一描述,其中的K为阶跃等效加速度a与地震计速度灵敏度S的乘积,ω0为固有角频率,D0为阻尼系数,从式(4)可见,当D0≤1时,r(t)的定义在实数域内将失去意义,式(4)只在D0 < 1时成立。
使用实际记录的地震计阶跃响应波形计算其响应频谱,通过式(2),采用最小二乘法在频域内拟合,可以方便、可靠地求得K、ω0、D0,其中ω0 = 2π/T0。本文关注重点是T0、D0,它们决定了地震计的低频特性。
1.3 地震计响应特性精确测定及H1(s)求取地震计传递函数包括幅频信息和相频信息。在普通的正弦标定中,无参考信号记录,只能测定幅频特性。利用本文方法进行正弦标定时,记录地震信号输出时,同步记录标定信号在测流电阻上产生的电压,处理正弦波标定信号可以同时获得地震计的振幅信息和相移信息。
任意一段正弦波形均可表示为
| $ w\left(t \right) = A\sin \left({\omega t + \varphi } \right)\;\;\;\;\;\;\;t \in \left[ {{t_0}, {t_1}} \right] $ | (6) |
在使用式(6)进行正弦波标定时,需要设定正弦波的频率和电流参数。电流参数可能受到恒流源精度和分流电路的影响,但频率只与采集系统的时钟频率有关,是高度精确的,因此可以把频率当成已知量来计算正弦波的振幅和周期。本文采用最小二乘法拟合求得精确振幅和相位值。在拟合中设定振幅精度目标为10-12,保证所求振幅和相位高度精确,满足正弦波标定数据处理的需要。地震计传递函数测定数据处理步骤如下。
(1)对每一个频率、每一个通道和测量电压的波形取出一段同步数据,使用正弦波拟合方法,得到同一段地震计3个分向和测流电压的振幅和相位。
(2)计算地震计输出各频点的3个方向的相位响应。电流流过标定线圈产生驱动力推定摆锤运动,力与加速度成正比,地震计输出与速度量成比例的电压。因此,地震计响应在指定频率点相位响应为
| $ {\varphi _r}\left(f \right) = {\varphi _s}\left(f \right) - {\varphi _I}\left(f \right) + \frac{{\rm{ \mathsf{ π} }}}{2} $ | (7) |
其中:φr为相位响应,φs为地震计输出信号相位,φI为标定电流相位。
(3)计算实际标定电流。用获得的测流电压除以测流电阻值即得到实际标定电流。
(4)计算地震计幅频特性。使用已有地震计输出3个分向各频率的振幅、标定灵敏度Sc和实测标定电流值,按式(8)计算地震计幅频特性。
| $ {A_r}\left(f \right) = \frac{{2{\rm{ \mathsf{ π} }}f{V_f}}}{{{S_c}{I_f}}} $ | (8) |
(5)计算地震计响应函数R(f)。将式(8)计算的地震计幅频特性带入式(9),可得
| $ R\left(f \right) = {A_r}\left(f \right)\cos {\varphi _r}\left(f \right) + j{A_r}\left(f \right)\sin {\varphi _r}\left(f \right) $ | (9) |
(6)计算所得地震计传递函数在各频点的实测值Hm(f )。
| $ {H_m}\left(f \right) = R\left(f \right)/\left| {R\left({{f_{{\rm{norm}}}}} \right)} \right| $ | (10) |
(7)拟合确定H1(s)。采用最优化方法拟合求H1(s),其目标函数为
| $ {\rm{Criteria}}\left({B, A} \right) = \sum\limits_{i = 1}^n {\left| {{H_m}\left(i \right) - {H_0}\left({{s_i}} \right) - {H_1}{{\left({{s_i}} \right)}^2}} \right|W\left(i \right)} $ | (11) |
其中,W(i)为对应频点的权重。在实际计算中,可对频带内数据优先保证拟合水平指定较高的权重,对频带外数据指定较小的权重;如无特定要求,可指定相同的非零权重。D0、ω0阶跃标定已确定,拟合的目标是确定A∈(an,an-1,...,a1,a0)、B∈(bm,bm-1,...,b1,b0)。
1.4 测试电路设计与普通地震计电标定不同,本文提出的测试方法引入测流电阻R,用于同步测试标定回路中的电流。实验中采用的电路见图 1,由标准EDAS-24GN地震数据采集器输出的电流标定信号依次流过测流电阻、地震计UD、EW、NS向的标定线圈后返回。地震计3个通道的输出信号输出到标准地震计数据采集器的A口3个主通道,测流电阻两端电压输出到地震数据采集器B口的某一通道(实测时选用第2通道)。当正弦标定电流流过标定线圈时,产生一个力作用在地震计摆锤上,地震计的响应波形由地震数据采集器记录下来,并同步记录测流电阻两端的电压信号。测流电阻两端的电压信号有2个作用,即精确计算实际流过标定回路的电流及作为测试地震计相位特性的参考信号。

|
图 1 精确测定地震计传递函数电路示意 Fig.1 The schematic diagram of measuring seismometer transfer function |
为验证所提出方法的可行性,首先测试标准地震计的传递函数。选定北京港震仪器设备有限公司生产的BBVS-120甚宽带地震计为标准地震计,其中-3 dB频带为120 s—50 Hz,标称灵敏度为2 000 V·s/m。该地震计灵敏度在振动台经过精确测试,并校正其标定灵敏度,数值分别为10.986 70、10.785 00、10.509 10。
2.1 实验仪器测试使用的标准数据采集器为一台6通道EDAS-24GN24高分地震数据采集器,其采集灵敏度经过标准信源校正,误差小于1/10 000。标准地震数据采集器共有6个信号输入通道,分别位于A、B端口。地震计及测试信号连接如图 1所示,2个端口的输入范围均设置为±20 V,采样率均设置为500 sps,采集器采用28位字长编码,电压分辨率在该设置下为149 nV。来自地震计和测流电阻端的电压信号经相同处理并记录下来,地震计输出信号与测流信号的差别与采集记录下来的信号差别相同。EDAS-24GN的6个通道同步采集数据,进行同步数据分析即可取得准确的仪器振幅和相位响应。
2.2 阶跃标定确定周期和阻尼向地震计发出阶跃响应,通过阶跃波形拟合获得地震计的周期和阻尼。阶跃波形上升侧频域、时间域的拟合见图 2,下降侧拟合与上升侧相似。阶跃拟合获得的地震计等校机械摆参数见表 1,由拟合结果可见,上升侧和下降侧拟合获得的参数高度一致。
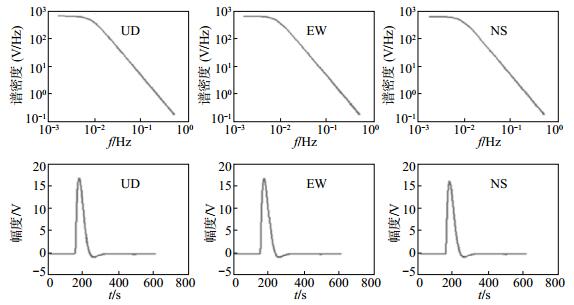
|
图 2 地震计阶跃标定波形拟合结果 Fig.2 The waveform fitting result of step calibration of the seismometer |
| 表 1 阶跃标定拟合得到等效机械摆参数 Tab.1 The equivalent mechanical pendulum parameters from step calibration |
向地震计发出如表 2所示标定参数的正弦波标定信号,信号参数在通带内尽量按5 mm/s的速度设计,在通带外适当增加,但在高频部分受采集系统标定信号幅度上限20 000 µA的限制,速度小于5 mm/s。在标定过程中,数据采集器自动波形使用记录波形,计算得到地震计3个分向输出和测流电压信号在各同频率点的幅度和相位,使用地震计输出电压和测流电压,并结合标定灵敏度,计算地震计的测试幅频响应和相频响应(图 3),实际测得的幅频响应值和相频响应值分别见表 3和表 4。
| 表 2 正弦波标定参数设计 Tab.2 Sine wave calibration parameters |

|
图 3 实测标准地震计频率特性 (a)地震计幅频特性;(b)地震计相频特性 Fig.3 The actual measured frequency characteristics of standard seismometer |
| 表 3 实际测得的地震计幅频响应值 Tab.3 The actual measured amplitude frequency response of the seismometer |
| 表 4 实际测得的地震计相频响应值 Tab.4 The actual measured phase frequency response of the seismometer |
按前文所述,标准传递函数表达式见式(1)、式(2)、式(3)所示,拟合传递函数的幅频特性和相频特性见图 4,标准地震计UD向、EW向和NS向传递函数拟合系数及残差分别见表 5—表 7。
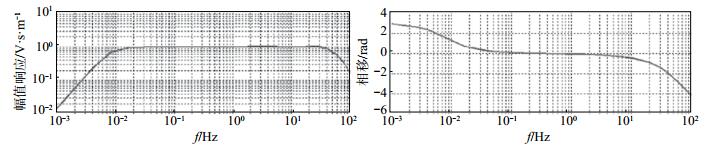
|
图 4 幅频特性和相频特性传递函数拟合结果 Fig.4 The fitted frequency characteristics of the seismometer transfer function |
| 表 5 标准地震计UD向传递函数拟合结果 Tab.5 The fitted result of the UD component of the seismometer transfer function |
| 表 6 标准地震计EW向传递函数拟合结果 Tab.6 The fitted result of the EW component of the seismometer transfer function |
| 表 7 标准地震计NS向传递函数拟合结果 Tab.7 The fitted result of the NS component of the seismometer transfer function |
(1)地震计传递函数低频、高频部分的关系及各自作用。图 5清楚显示地震计传递函数可以分为低频段和高频段2个部分,其中低频段由其等效机械摆的周期和阻尼决定,高频段通过拟合求得。低频段和高频段综合在一起形成地震计的整体传递函数。
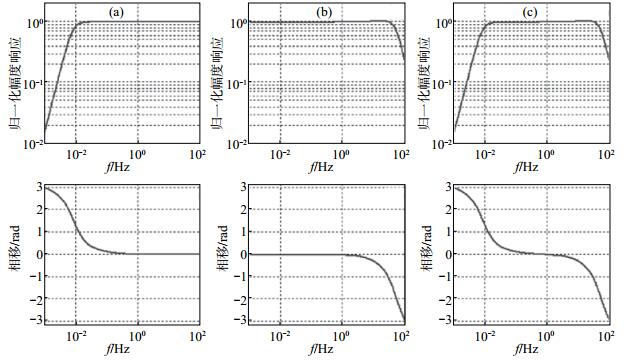
|
图 5 拟合结果显示的低频段、高频段和综合频率特性 (a)低频段传递函数的幅频特性和相频特性;(b)传递函数高频段的幅频特性和相频特性;(c)综合幅频特性和相频特性 Fig.5 The fitted result of the low frequency band, high frequency band and full frequency band |
(2)拟合结果的多解性及最终结果选取。根据选择的参数不同,同一频率特性可以有多个传递函数表达式,这些表达式在形式上是有差别的,是实际测量数据拟合得到的结果,只要与实际数据吻合,均可作为地震计传递函数。在实际工作中应当选用与实际数据拟合残差小于一定水平范围内最短数据长度的拟合结果。
(3)名义电流和实际电流误差对测试的影响。表 8给出本实验中名义电流与实际电流的偏差,其平均相对偏差为-1.533%。在低频段,偏差与电流大小有关,主要是因为电流档位变化,改用不同电路,电路之间存在差异。在电流达到满刻度值后,电流明显有规律的变小,主要是标定信号发生器D/A转换采样率固定,当频率升高时,每个周期内样点减少所致。
| 表 8 名义标定电流和实际标定电流偏差 Tab.8 The deviation of nominal calibration current and actual calibration current |
(4)频率特性的几种形式及转换。地震计传递函数有3种形式:①幅频、相频特性数据列表;②s算子的多项式商;③零极点形式。本文已明确证明可以通过拟合把幅频、相频特性列表数据转换为s算子的多项式商,进一步假定分母多项式和分子多项式为0,求出各自的解,得到传递函数的零极点。表 9为利用该方法求得的1组垂直向零极点。
| 表 9 垂直向4零点、7极点模式下的零极点 Tab.9 The zero-pole parameters of the UD component |
若必要,也可按式(13)把零极点转换成传递函数,进一步代入式(14)计算各频点的复数响应,计算幅频响应和相频响应。
| $ h\left(s \right) = \frac{{\prod\limits_{j = 1}^{{N_{\rm{z}}}} {\left({s - {z_j}} \right)} }}{{\prod\limits_{i = 1}^{{N_{\rm{p}}}} {\left({s - {p_i}} \right)} }} $ | (13) |
| $ s = j2{\rm{ \mathsf{ π} }}f $ | (14) |
(5)其他类型地震计测试结果。为验证方法的普适性,选取1台北京港震仪器设备有限公司开发的GL-CS60宽频带地震计和1台FSS-3M短周期地震计进行传递函数对比测试。选择3零点、6极点模式,测试结果见表 10,可见拟合结果较好。GL-CS60是斜轴悬挂三分向地震计,通过变换后得到UD、EW、NS分向的输出,标定时以斜轴方式输出,得到斜轴地震计传递函数。
| 表 10 GL-CS60宽频带、FSS-3M短周期地震计实测传递函数 Tab.10 The actual measured transfer function of GL-CS60 and FSS-3M |
综上所述,可知本文提出的使用阶跃标定和正弦标定测定地震计传递函数的方法,具有以下特点。
(1)本文提出联合使用阶跃标定和正弦波标定测定地震计传递函数的方法,只需要1台6通道地震计采集器和1条经过修改的摆线,采用数据采集器固有功能即可完成地震计传递函数测试,具有操作简单、容易实现、结果置信度、精度高的特点。
(2)本文提出的地震计传递函数测量方法与伪随机码标定方法相比,具有信号频点信噪比高、结果可靠的特点,拟合结果准确,直接反映地震计的频率特性高。
(3)本文提出的方法采用的目标函数和传递函数形式考虑到地震计传递函数的特点,拟合结果物理意义明确,测试结果说明低频段受等效机械摆自振周期和阻尼控制,高频段取决于地震计滤波器特性。
(4)本文提出的方法具有普适性,可以用于甚宽带地震计、宽带地震计、短周期地震计的传递函数测试。
| 李海亮. 地震计阻尼和自振频率的频域测定[J]. 地震地磁观测与研究, 2000, 21(2): 7-12. | |
| 林湛, 薛兵, 朱小毅, 等. 地震计的改进型伪随机二进制标定方法[J]. 地球物理学进展, 2015, 30(3): 1151-1158. DOI:10.6038/pg20150319 | |
| 王广福. 地震观测系统的标定与检查[M]. 北京: 地震出版社, 1986, 165-170. | |
| Berg E, Chesley D M. Automated High-Procision Amplitude and Phase Calibration of Seismic System[J]. BSSA, 1976, 66(4): 1413-1424. | |
| Berger J, Agnew D C, Parker R L, Farrell W E. Seismic system calibration:2. cross-spectral calibration using random binary signal[J]. BSSA, 1979, 69(1): 271-288. | |
| Bolduc P M, Ellis R M, Russell R D. Determination of the seismograph phase response from the amplitude response[J]. BSSA, 1972, 62(6): 1665-1672. | |
| Bormann P. New Manual of Seismological Observatory Practice (NMSOP-2)[M]. Potsdam: GeoForschungs Zentrum, 2002, 34-40. | |
| Kim W Y, Ekström G. Instrument Responses of Digital Seismographs at Borovoye, Kazakhstan, by inversion of transient calibration pulses[J]. BSSA, 1996, 86(1A): 191-203. | |
| Peterson J, Hutt C R, Holcomb L G. Test and Calibration of the Seismic Research Observatory[M]. USGS Open-File Report, 1980, 80-187. | |
| Rodgers P W, Martin A, Haver M R, et al. Signal-coil Calibration of Electromagnetic Seismometers[J]. BSSA, 1995, 85(3): 845-850. |
 2018, Vol. 39
2018, Vol. 39
