钻孔应变仪分为体应变仪(Sacks I S et al,1971;苏恺之等,2003)和分量式应变仪(欧阳祖熙等, 1988, 2009;邱泽华等,2004;邱泽华,2010;李海亮等,2010;牛安福等,2011),后者具有方向性,克服了前者的盲向性特点,近十年逐步成为国际上进行地壳岩石应变相对连续测量使用的主流仪器。2003年美国开始实施板块边界观测计划(PBO)(张宝红, 2004, 2010),沿圣安德烈斯断层和阿拉斯加南部地区建立85个钻孔应变台站,使用Gladwin改进型分量式应变仪(在原有三分量应变仪基础上添加一个分量元件)进行观测,获得一批观测资料(Roeloffs E,2010;刘序俨等,2014)。中国自主研制的四分量应变仪分为RZB、YRY和SKZ等3种型号,2007年以后在地震重点监测区建立60余个测点。此外,建有80余口体应变观测井,其中大部分配备国产TJ型体应变仪,少量配备美国产Sacks-Evertson型应变仪。由于岩石应变不能直接进行观测,必须经过钻孔(一般几十米至上百米深)、放入应变仪探头并用膨胀水泥(或改性的普通水泥)与岩石耦合(焊接)(保证应力与位移在边界上连续)后才能测量,故人为形成一个显著的附加应力场,导致探头钢筒所受压应力并不等于钻孔周围岩石的围压,需要一个传递系数与之关联。理想情况下,假定钻孔周围岩石压应力分布均匀,则由钢筒、水泥和岩石组成的3层圆环应变观测系统可以看作是轴对称问题,根据弹性力学中的厚壁圆筒方程(杨绪灿等,1987),张凌空等(2013)研究了该系统应力与应变的关系。利用该结果,本文进一步推导压应力传递系数计算公式,分析应力的传递过程和影响因素。这对应变仪有关力学参数设计及观测资料分析具有指导意义。
1 岩石压应力传递系数计算不同型号的应变仪基本工作原理相同。考虑到地壳上部岩石大部分以水平应力为主导,可设一块无限大的岩石平板,平板中有一半径为r3(一般为65 mm或76 mm)的钻孔,安置其中的应变仪钢筒内半径为r1,外半径为r2,通过膨胀水泥与岩石耦合(焊接),以此保证应力和位移分量在边界上连续。设钢筒、水泥、岩石的弹性模量和泊松比分别为E1、μ1、E2、μ2、E3、μ3。假定钻孔所处介质近似为各向同性弹性体,遵从虎克定律,且井口及井底对传感器的影响可以忽略,钻孔的轴向应力为0。为了研究方便,想象在钻孔周围有一个外半径为r0(r0≫r3)的巨大圆环,其外边界受法向均匀分布的压应力P3作用,内边界即孔壁承受的均匀内压力为P2,则水泥层所受均匀外压力为P2、内压力为P1,应变仪钢筒所受均匀外压力为P1、内压力为0(图 1)。若不计自重,则该应变观测系统属于典型的轴对称问题,根据厚壁圆筒方程(杨绪灿等,1987),张凌空等(2013)推导得出
|
图 1 钻孔应变观测3层介质力学模型 Fig.1 Three layer medium mechanics model of borehole strain observation |
| $ k = \frac{{{\varepsilon _{\rm{m}}}}}{{{\varepsilon _{{\rm{m0}}}}}} = \frac{{r_2^2{E_3}{P_1}}}{{\left({r_2^2 - r_1^2} \right){E_1}{P_3}}} $ | (1) |
式中,k是应变仪钢筒内壁面应变(εm)与空孔岩石面应变(εm0)之比,有
| $ k = {x_4}{E_3}/{E_1} $ | (2) |
其中
| $ {x_4} = \frac{{r_2^2r_3^2\left({{\alpha _2} + {\beta _2}} \right)\left({{\alpha _3} + {\beta _3}} \right)}}{{r_2^2\left({{\alpha _2} - {\alpha _3}} \right)\left[ {r_1^2\left({{\alpha _1} + {\beta _2}} \right) + r_2^2\left({{\beta _1} - {\beta _2}} \right)} \right] + r_3^2\left({{\alpha _3} + {\beta _2}} \right)\left[ {r_1^2\left({{\alpha _1} - {\alpha _2}} \right) + r_2^2\left({{\alpha _2} + {\beta _1}} \right)} \right]}} $ | (3) |
式中,各系数分别为:α1 = (1 + μ1)/E1,α2 = (1 + μ2)/E2,α3 = (1 + μ3)/E3,β1 = (1-μ1)/E1,β2 = (1-μ2)/E2,β3 = (1-μ3)/E3。
根据式(1),可推得
| $ \tau = {P_1}/{P_3} = \left({r_2^2 - r_1^2} \right){E_1}k/\left({r_2^2{E_3}} \right) = \left[ {1 - {{\left({{r_1}/{r_2}} \right)}^2}} \right]k\;{E_1}/{E_3} $ | (4) |
显然,τ为外围岩石(P3)通过岩石圈和水泥层向钢筒外壁(P1)的压应力传递系数,故P1 = τ P3。将式(2)代入式(4),τ又可表述为
| $ \tau = \left[ {1 - {{\left({{r_1}/{r_2}} \right)}^2}} \right]{x_4} $ | (5) |
同理,定义外围岩石向空孔岩石内壁的压应力传递系数为τs = P2/P3,岩石空孔内壁通过水泥层向钢筒外壁的压应力传递系数为τ0 = P1/P2,故τ实际为2个应力传递系数的乘积,即
| $ \tau = {P_1}/{P_3} = \left({{P_2}/{P_3}} \right)\left({{P_1}/{P_2}} \right) = {\tau _{\rm{s}}}{\tau _0} $ | (6) |
有兴趣的学者可以根据张凌空等(2013)的研究推导τs和τ0的计算式。
令r21 = r2/r1, r31 = r3/r1,E21 = E2/E1,E31 = E3/E1,则由式(5)可得
| $ \tau = \left[ {1 - {{\left({1/{r_{21}}} \right)}^2}} \right]{x_4} $ | (7) |
据张凌空等(2013)的研究,则x4为
| $ {x_4} = 4r_{21}^2\;r_{31}^2/\left({{E_{21}}\;{E_{31}}Z} \right) $ | (8) |
其中
| $ \begin{array}{l} Z = r_{21}^2\left({\frac{{1 + {\mu _2}}}{{{E_{21}}}} - \frac{{1 + {\mu _3}}}{{{E_{31}}}}} \right)\left[ {1 + {\mu _1} + \frac{{1 - {\mu _2}}}{{{E_{21}}}} + r_{21}^2\left({1 - {\mu _1} - \frac{{1 - {\mu _2}}}{{{E_{21}}}}} \right)} \right] + \\ \;\;\;r_{31}^2\left({\frac{{1 - {\mu _2}}}{{{E_{21}}}} + \frac{{1 + {\mu _3}}}{{{E_{31}}}}} \right)\left[ {1 + {\mu _1} - \frac{{1 - {\mu _2}}}{{{E_{21}}}} + r_{21}^2\left({1 - {\mu _1} + \frac{{1 + {\mu _2}}}{{{E_{21}}}}} \right)} \right] \end{array} $ | (9) |
由式(7)—式(9)可知,本质上τ不是与r1、r2、r3和E1、E2、E3的绝对值有关,而是与它们之间的比值有关。根据式(4)、式(7),可以从不同角度对τ值进行解析。
2 压应力传递系数(τ)影响机制 2.1 τ与岩石弹性模量、泊松系数及钢筒内半径的关系以中国目前使用较多的YRY-4型分量式应变仪观测孔为例,其参数分别为r1 = 51.5 mm,r2 = 53.5 mm,r3 = 65 mm,E1 = 19.6×1010 Pa,μ1 = 0.3,E2 = 3×1010 Pa,μ2 = 0.25,当μ3分别为0.1、0.2、0.3、0.4时,根据式(4)绘制τ值随E3的变化曲线,见图 2(a),图中4条曲线自上而下μ3值分别为0.1、0.2、0.3、0.4。可以看出,当各项参数均为定值时,τ随岩石弹性模量(E3)和泊松系数(μ3)的增大而下降,不同的是,τ受E3影响显著,受μ3影响较弱,且当E3>4×1010 Pa时,μ3数值大小对τ值的影响已无明显差别。故岩石越硬、越不易弹性变形时τ值越小。

|
图 2 τ与岩石、水泥的弹性模量(E3、E2)和泊松系数(μ3、μ2)及钢筒内半径(r1)的关系 Fig.2 The relationship between τ and elastic modulus of rock, cement (E3, E2) and Poisson's coefficient (μ3, μ2) and steel cylinder radius (r1) |
应变仪钢筒与岩石孔壁的耦合大多使用专用的低热量膨胀水泥粘接(苏恺之等,1987),因施工过程中搅拌水泥时加水量存在一定变化,因此实际的弹性模量和泊松系数与实验室中测得的标准数值可能有某种程度的偏差,有必要研究E2、μ2的改变对τ值可能产生的影响。若取E3 = 5×1010 Pa,μ3 = 0.25,则图 2(b)(图中4条曲线自上而下分别μ2值分别为0.1、0.2、0.3、0.4)表明,当E2<2.1×1010 Pa时,τ随E2的增加而增大,反之下降;当E2不变时,τ随μ2增加而减小。一般施工工艺要求将E2控制在(2.5—4)×1010 Pa之间(苏恺之等,1987),则τ平均最多减小0.012。可知,E2、μ2的改变对τ影响较小。
2.3 τ与钢筒内半径或壁厚的关系假定r3 = 65 mm,r2 = 53.5 mm不变,即水泥层厚度不变,研究r1改变,即钢筒壁厚(n = r2-r1)改变对τ值的影响。取E3 = 5×1010 Pa,μ3 = 0.25,E2 = 3×1010 Pa,μ2=0.25,图 2(c)显示,当r1逐渐增大,即钢筒壁相应变薄时(n减小),τ逐渐下降,且影响较为显著。
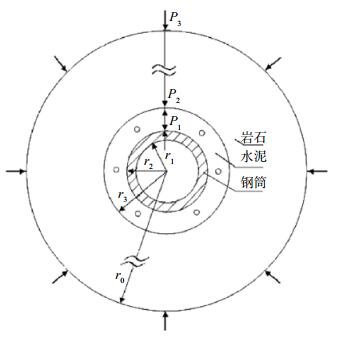
2.4 τ与E3/E1和E2/E1的关系取r21= r2/r1= 53.5/ 51.5 = 1.039,r31= r3/r1 = 65/51.5 = 1.262,根据式(7)可以绘制τ值与E3/E1和E2/E1的关系曲线,见图 3(a),图中4条曲线自上而下分别为E2/E1 = 0.10、0.15、0.20、0.25,可知τ随E3/E1和E2/E1的增加而减小,但前者影响显著,后者影响较小,且当E3/E1>0.26时,E2/E1数值的大小对τ值的影响已无明显差别。
|
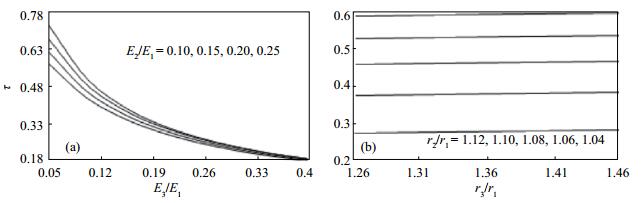
图 3 τ与E3/E1、E2/E1及r3/r1、r2/r1的关系 Fig.3 The relationship between τ and E3/E1, E2/E1 and r3/r1 and r2/r1 |
取E21 = E2/E1 = 3/19.6 = 0.153 1,E31 = E3/E1 = 5/19.6 = 0.255 1,根据式(7)绘制τ与r3/r1和r2/r1的关系曲线,见图 3(b),图中5条曲线自上而下r2/r1分别为1.12、1.10、1.08、1.06、1.04,可知τ随r3/r1的增加而缓慢增大,随r2/r1的增加而显著增大。
3 结论综上所述,可以得出以下结论。
(1)钻孔外围岩石(P3)通过水泥层向应变仪钢筒外壁(P1)的压应力传递系数可表述为τ = P1/P3 = [1-(r1/r2)2] k E1/E3,故P1 = τ P3,其中k为钢筒内壁面应变与空孔岩石面应变之比,是与观测系统(岩石、水泥、钢筒)的各项参数均有关的常数。通常,τ ≈ 0.182 0—0.719 5<1,故P1<P3,即岩石压应力在传递过程中会有所衰减,τ实际反映了P3的传递效率。
(2)τ随岩石弹性模量(E3)和泊松系数(μ3)的增大而下降;水泥弹性参数(E2、μ2)的改变对τ影响较小;钢筒内半径(r1)增大或壁厚变薄时,τ值显著下降;τ随E3/E1和E2/E1的增加而减小,随r3/r1及r2/r1的增加而增大。
(3)由于基岩并非均匀完整,探头与孔壁耦合也不完善,在实际测量中,岩石压应力沿钻孔可能不是均匀分布,理论计算结果可能存在误差,但因钻孔孔径较小(通常r3 ≤ 76 mm),估计误差不会太大,有待今后进一步验证。
(4)井下岩石弹性参数的测定是一项重要的基础工作,钻孔应变观测的有关理论计算经常要用到它,但目前绝大多数台站未开展该项工作。为了充分利用钻孔应变观测资料,建议安装应变仪探头时,相关单位能给予足够的资金支持,以保障科研任务的顺利开展。
| 李海亮, 李宏. 钻孔应变观测现状与展望[J]. 地质学报, 2010, 84(6): 895-900. | |
| 刘序俨, 王紫燕, 方宏芳. 对当前四分量钻孔应变观测的审视——以应变不变量为标尺[J]. 地球物理学报, 2014, 57(10): 3332-3346. DOI:10.6038/cjg20141020 | |
| 牛安福, 张凌空, 闫伟, 等. 中国钻孔应变观测能力及在地震预报中的应用[J]. 大地测量与地球动力学, 2011, 31(2): 48-52. | |
| 欧阳祖熙, 张宗润. 钻孔应变仪与井壁耦合方法的研究[M]//赵国光. 地壳构造与地壳应力文集(2). 北京: 地震出版社, 1988. | |
| 欧阳祖熙, 张钧, 陈征, 等. 地壳形变深井综合观测技术的新进展[J]. 国际地震动态, 2009, 11061106(1): 1-13. | |
| 邱泽华, 石耀霖. 国外钻孔应变观测的发展现状[J]. 地震学报, 2004, 26(Z1): 162-168. | |
| 邱泽华. 中国分量钻孔地应力-应变观测发展重要事件回顾[J]. 大地测量与地球动力学, 2010, 30(5): 42-47. | |
| 苏恺之, 刘瑞民, 裴玉珍, 等. 体积式钻孔应变仪与岩孔的耦合技术[M]//国家地震局地壳应力研究所. 地壳构造与地壳应力文集(1). 北京: 地震出版社, 1987. | |
| 苏恺之, 李海亮, 张均, 等. 钻孔地应变观测新进展[M]. 北京: 地震出版社, 2003. | |
| 张宝红. 美国的板块边界观测(PBO)计划[J]. 大地测量与地球动力学, 2004, 24(3): 105-108. | |
| 张宝红. 美国板块边界观测(PBO)中的钻孔应变观测设备[J]. 大地测量与地球动力学, 2010, 30(Z2): 40-44. | |
| 张凌空, 牛安福. 钻孔体应变与面应变观测参数k的计算[J]. 中国地震, 2013, 29(3): 335-346. | |
| Roeloffs E. Tidal calibration of Plate Boundary Observatory borehole strainmeters:Roles of vertical and shear coupling[J]. J Geophys Res, 2010, 115(B6): B06405 | |
| Sacks I S, Suyehiro S, Evertson D W. Sacks-Evertson strainmeter, its installation in Japan and some preliminary results concerning strain steps[J]. Proceedings of the Japan Academy, 1971, 47(9): 707-712. |
 2018, Vol. 39
2018, Vol. 39