地震观测是研究地震和地球内部结构的重要手段,也是地震学理论体系建立和发展的重要基础,数字地震记录已成为现代地震研究的基石。地震仪系统是一种线性动力学系统,线性系统所具有的叠加原理和频率保持等特性,在地震观测工作中具有重要作用。地震仪系统特性可用线性动力学系统理论描述,在工程分析中,线性系统的频域分析是频域内研究系统性能或输入输出信号关系的一种方法,不仅可以间接地揭示系统某些性能是否符合要求,还能够求得动态信号中各个频率成分的幅值分布和能量分布,从而得到主要幅度和能量分布的频率值。地震仪频率响应和地动噪声分析是地震观测中的重要概念,频率响应是地震计的主要技术指标之一,频响特性曲线能够直接证明地震计带宽指标等是否符合要求。地动噪声可近似为一个平稳随机信号过程,因此可采用功率谱密度函数进行分析,反映台址各频段台基噪声水平,在台站勘选及降噪滤波器设计等方面具有重要作用。Matlab集合数值分析、矩阵计算、科学数据可视化及非线性动态系统的建模和仿真等功能,在控制、通信、信号处理及科学计算等领域中得到广泛应用(张志涌,2011)。
本文在系统频率响应及功率谱密度函数等内容中引入地震仪系统技术方面的解释,并结合实际工作,使用Matlab完成地震计频率特性和地动噪声功率谱计算。
1 频域分析原理 1.1 地震仪频率响应频谱分析是利用傅里叶方法对信号进行分解,进而进行研究和处理的一种过程,对于一个系统来说,频率特性是指幅频特性和相频特性,也称频率响应。线性系统引起的信号失真可由以下因素造成:①系统对信号中各频率分量幅度产生不同程度的衰减,使响应各频率分量的相对幅度产生变化,造成幅度失真;②系统对各频率分量产生的相移与频率不成正比,使输出的各频率分量在时间轴上的相对位置产生变化,造成相位失真。因此,通过系统的频率响应,可以判断一个系统是否符合工作要求。
地震仪系统的动态特性在线性范围内,与任何线性时不变系统一样,可用线性微分方程、拉普拉斯传递函数、复频率响应函数和系统的脉冲响应来描述。线性系统同时满足叠加性和均匀性,其中:叠加性是指当几个输入信号同时作用到系统时,总的输出是每个输入信号单独作用产生的和;均匀性是指当输入信号乘以一个常数时,输出是原单个信号输入时对应的输出乘以相同常数。一个稳定的线性定常系统或环节,当系统输入为正弦信号r(t) = A1sin(ωt + φ1)时,其稳态输出也为同频率正弦信号,记为c(t) = A2sin(ωt + φ2),只是振幅与相角不同,并且A2、φ2均为频率ω的函数,即A2(ω)、φ2(ω)。将2个信号的振幅比定义为系统的幅频特性,相位差定义为系统的相频特性,则
| $ \begin{array}{l} 幅频特性\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A\left(\omega \right) = {A_2}\left(\omega \right)/{A_1}\\ 相频特性\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\varphi \left(\omega \right) = {\varphi _2}\left(\omega \right) - {\varphi _1} \end{array} $ | (1) |
二者合称为系统的复频率特性。
输入输出信号通过欧拉公式可以用指数式或极坐标式来表示。因此,结合式(1),输入、输出信号的比值表示为
| $ \begin{array}{l} G\left({j\omega } \right) = A\left(\omega \right){e^{j\varphi }}\left(\omega \right)\\ G\left({j\omega } \right) = A\left(\omega \right)\angle \varphi \left(\omega \right) \end{array} $ | (2) |
由定义可知:A(ω) = |G (jω)|,φ(ω) =∠G (jω)。
频率特性表示稳定系统在正弦信号输入下,其稳态输出与输入之间的关系。利用频率特性容易求得稳定系统在正弦信号输入下的稳态输出(胡寿松,1994),即A2 = A (ω)·A1,φ2 = φ (ω) +φ1。
1.2 地震台站功率谱密度函数功率谱密度函数描述随机信号的频率构成,在频率域描述时,周期信号可以用各个频率分量有效值描述,在一定带宽内只有一个频率分量的谐振动,而随机信号在一定频带内测得的有效值则依赖于带宽,故频域随机信号不宜用有效值表示,需用功率密度函数表示。经典谱估计的基本方法有(Wunsch D C et al,1968):①对原始数据直接进行傅里叶变换;②对相关函数做傅里叶变换。
本文对记录数据的计算处理分析采用方法①——周期图法(直接法)。该方法把随机信号x(n)的N点观测数据xN (n)视为能量有限信号,直接取x(n)的傅里叶变换(邵玉平等,2007)(在对数据进行功率谱估计时,先将去除直流分量和采用窗函数的数据进行离散傅里叶变换,取其幅值的平方,并除以N)。用周期图法估计的功率谱计算公式为
| $ \hat P\left({{e^{j\omega }}} \right) = \frac{1}{N}{\left| {{X_N}\left({{e^{j\omega }}} \right)} \right|^2} $ | (3) |
式中:XN (ejω)为观测数据x(n)的傅里叶变换值。
周期图概念早在1899年就已提出,但由于点数N一般比较大,计算量过大,在当时无法使用,1965年FFT出现后,成为谱估计的一种常用方法。
2 利用Matlab进行频域分析 2.1 Bode图和Bode函数Bode图又称对数频率特性图,由2部分组成:①对数幅频特性曲线;②对数相频特性曲线。Bode图横坐标通常以ω为横轴变量,并采用ω的对数值刻度进行标注,变化范围较广(施梨,2015)。幅值和相位的Bode图横坐标均采用ω表示,纵坐标分别采用L(ω) = 20lg|G(jω)|或φ(ω) = ∠G (jω)表示。
对数坐标具有以下优点:①对数幅频特性以dB为单位,减小了L(ω)曲线的斜率,便于在更宽频率范围内研究系统的频率特性;②可以用折线法快速绘制系统近似的幅频特性,便于对系统进行分析和综合校正;③由于横坐标采用对数刻度,可大范围扩展横轴频率范围,又不降低低频段特性的准确性。
Matlab提供的Bode函数可以直接求取、绘制给定线性系统的Bode图。当Bode命令不包含左端返回变量时,函数运行后在屏幕上直接绘制Bode图。如命令表达式的左端含有返回变量,Bode函数计算出的幅值和相角将返回相应矩阵,屏幕上不显示频率响应图,因此可通过相应的调用命令,取出对应幅值或相角信息进行计算,命令的调用格式为
[mag, phase, w] = bode(num, den)
[mag, phase, w] = bode(num, den, w) 或[mag, phase, w] = bode(G)
[mag, phase, w] = bode(G, w)
矩阵mag、phase包含幅值和相角信息,由给定频率点计算得到。不指定频率ω时,Matlab自动产生ω向量,并根据ω向量上各点计算幅值和相角。相角是度来表示,幅值为增益值,绘制Bode图时需转换成分贝值,可由magdb = 20log10(mag)命令执行。
2.2 地震计幅频特性和地动噪声功率谱计算BBVS-60宽频带地震计和CMG-3ESP宽频带地震计具有频带宽、灵敏度高、动态范围大的特点,传递函数稳定。目前,2种类型地震计在中国区域地震监测台网使用广泛。根据厂家给定的地震仪传递函数和零极点,借助Matlab,可获得设备的频响曲线,进而直观对比设备是否符合工作要求或多种设备的频响差异。
CMG-3ESP和BBVS-60地震计的零极点和归一化因子(戴伳贵,2009)见表 1。
| 表 1 CMG -3ESP、BBVS -60地震计零极点和归一化因子 Tab.1 Zeros poles and normalization factor of CMG-3ESP and BBVS-60 seismograph |
地震计零极点在复平面位置的分布对地震计性能有较大影响,一个稳定线性动态系统传递函数的所有极点均必须位于复S平面的左半平面。从上述2种类型地震计的零极点值可知,系统极点、零点均位于S平面的左半平面,可见2种类型的地震计系统是稳定的最小相位系统。因此,地震观测系统的动力特性可以由系统的幅频特性和相频特性来描述。
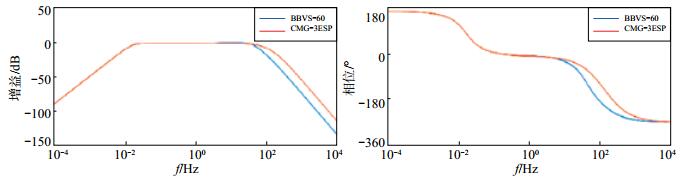
执行Matlab计算程序可得到2种类型地震计的频率响应曲线,见图 1,从图中可以获知地震计工作频带范围,理论上2类地震计在工作频带内频响曲线具有较好的一致性。部分代码如下
|
图 1 BBVS-60和CMG-3ESP地震计频响曲线 Fig.1 Frequency response curve of the BBVS-60 and CMG-3ESP seismograph |
[num1, den1]=zp2tf(z1, p1, k1);
sys1=tf(num1, den1);
bode(sys1);
在地震观测系统中,地面运动检测由地震计来完成。利用惯性摆检测地面运动,通过换能器将摆的运动转换为电压信号,电压信号经过一系列放大和滤波,通过数据采集器将连续的电压信号数字化,得到离散的数字信号,在数字化记录文件中,波形数据的单位是counts,通过对记录counts值的转换,可得到相应的地动速度和地动加速度,转换公式(中国地震局监测预报司,2003)如下。
| $ 地动速度\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{X_v} = {A_{v0}} \times {K_{{\rm{ad}}}}/\left({G \times {S_{{\rm{s0}}}}} \right) $ | (4) |
| $ 地动加速度\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{X_a} = \omega \times {A_{v0}} \times {K_{{\rm{ad}}}}/\left({G \times {S_{{\rm{s0}}}}} \right) $ | (5) |
式中:ω = 2πf;Xv为地动速度,单位m/s;Av0为振幅值,单位counts;Kad为A/D转换因子,单位为V/counts;G为前置放大增益;Ss0为地震计电压灵敏度,单位V/m·s-1。
噪声功率谱分析可估计各个台址上噪声信号能量集中频段,在台站选址、降噪数字滤波器设计及提高记录地震信号信噪比等方面具有重要作用(陈祥熊等,1998)。为了得到真实地动噪声功率谱密度,需要对数据进行仪器响应预扣除,以消除地震计影响,由公式(3)(徐嘉隽,2013)扣除地震仪器频率响应后,得到实际地噪声功率谱密度函数。
| $ P\left({{e^{j\omega }}} \right) = \hat P\left({{e^{j\omega }}} \right)/{\left| {G\left({j\omega } \right)} \right|^2} $ | (6) |
式中:G (jω)为地震计复频率特性。
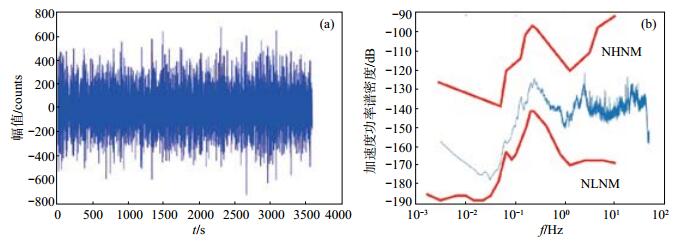
选取四川省油榨坪台2015年6月25日00时00分开始记录的垂直向1小时连续波形数据作为样本,进行地动噪声功率谱计算(选取时段相对安静,无中断和干扰),原始波形及噪声功率谱曲线见图 2。图 2(b)中NHNM和NLNM分别代表全球高噪声和低噪声模型,噪声模型是评价地球上一个地震台站噪声水平的基本标准,通过台站背景噪声PSD曲线与新的全球噪声模型对比,直观可见特定频率范围内噪声分布情况。
|
图 2 垂直向原始信号波形及噪声功率谱曲线 (a)原始信号波形;(b)噪声功率谱 Fig.2 Original signal waveform and power spectra of noise of vertical component |
通过对选取的波形数据进行计算,得出1/3倍频程带宽(1—20 Hz)地动噪声RMS值为:UD向:1.88×10-8 m/s;EW向:1.91×10-8 m/s;NS向:2.0×10-8 m/s。根据地震台站观测环境技术要求规定,可知地动噪声水平Enl < 3.16×10-8 m/s,应为Ⅰ级环境地噪声水平。由图 2(b)也可看出,该台站地动噪声功率谱曲线在频带范围内仅比全球低噪声模型NLNM值高5—25 dB,可知油榨坪台在此时间段环境背景噪声水平较低。根据计算公式编写地动噪声功率谱计算代码,部分代码为
z=[0;0];
p=[-7.40159e-02+7.40159e-02i;-7.40159e-02-7.40159e-02i;...
-1.0053088e+03; -5.026544e+02;...
-1.1309274e+03];
k=+5.76e+8;
[num, den]=zp2tf(z, p, k);
sys1=tf(num, den);
[mag phase]=bode(sys1, 2*pi*f);
mag1(1:nfft/2+1)=mag(1, 1, 1:nfft/2+1);
mag1=mag1.*mag1;
pxx2=pxx2./abs(mag1');
3 结束语本文在系统频率特性分析中引入地震仪技术方面的解释,阐述了地震仪系统作为稳定、线性定常系统所具有的幅频特性以及功率谱密度函数、地震仪器输出信号处理等内容。并通过实例,借助Matlab软件,绘制原始信号波形和噪声功率谱曲线,进而对所得结果进行分析。本文所介绍的内容可用于地震仪系统工作原理分析及异常波形形态物理机制研究和产出数据的处理,同时可为地震计频响特性计算、地震台站勘选噪声水平测试分析提供参考。
| 陈祥熊, 陈文明, 江燕, 等. 福建数字地震台网台址背景噪声分析[J]. 地震地磁观测与研究, 1998, 19(5): 13-22. | |
| 戴伳贵, 谌亮, 康宏, 等. CMG-3ESPC宽频带地震计稳态标定和传递函数构建[J]. 四川地震, 2009, 11061106(3): 12-15. | |
| 胡寿松. 自动控制原理[M]. 北京: 国防工业出版社, 1994. | |
| 邵玉平, 韩进, 宋澄. 向家坝数字遥测地震台网的台基地噪声分析[J]. 地震地磁观测与研究, 2007, 28(2): 61-64. | |
| 施梨. Matlab工程仿真与应用30例[M]. 北京: 电子工业出版社, 2015. | |
| 徐嘉隽. 福建测震台网测震台站环境地噪声水平[J]. 地震地磁观测与研究, 2013, 34(1/2): 101-105. | |
| 张志涌. 精通Matlab R2011a[M]. 北京航空航天大学出版社, 2011. | |
| 中国地震局监测预报司. 数字地震观测技术[M]. 北京: 地震出版社, 2003. | |
| Wunsch D C, Bell R R. Determination of threshold failure levels of semiconductor diodes and transistors due to pulse voltages[J]. IEEE Transactions on Nuclear Science, 1968, 15(6): 244-259. DOI:10.1109/TNS.1968.4325054 |
 2018, Vol. 39
2018, Vol. 39