2. 中国哈尔滨 150080 中国地震局工程力学研究所
2. Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China
强震动观测可为抗震设防、地震区划等地震工程研究领域提供科学观测数据,在地震预警、烈度速报与地震应急工作中也发挥着重要作用(赵希磊等,2014)。强震动观测数据不仅受观测系统影响,还受到台站所在区域场地与外部环境噪声等影响,有必要研究强震动台站的区域场地响应特征、台站背景噪声及二者之间的联系。本文针对安徽省部分强震动台站记录的观测数据,采用H /V谱比法和噪声功率谱密度函数,依次分析台站的场地响应与背景噪声水平,并进行对比分析。
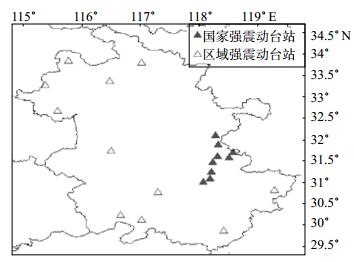
1 台网布局与仪器性能安徽省强震动台网拥有20个强震动观测台站,其中9个国家强震动台站、11个区域强震动台站,台站分布见图 1。在中国地震局“十五”重点项目建设期间,安徽省沿长江临近江苏区域建成9个国家强震动观测台站,同时完成2个国家测震台和1个区域测震台的测震、强震综合观测升级;在安徽省地震局“十二五”项目建设期间,新建8个区域测震、强震综合观测台站。
|
图 1 安徽省强震动台站分布 Fig.1 The distribution of the strong motion stations in Anhui Province |
安徽省强震台站主要采用中国地震局工程力学研究所研发的SLJ-100强震计和北京港震机电技术有限公司生产的BBAS-2型强震计,采用中国地震局工程力学研究所研发的GDQJ2型强震数据记录器与北京港震机电技术有限公司生产的EDAS-24GN数据采集服务器进行数据采集。9个国家强震动台站有关基本参数见表 1。
| 表 1 安徽省国家强震动台站信息 Tab.1 The basic information of the China strong motion stations in Anhui Province |
强震动台站获取的信号受振动源、振动传播路径、观测仪器和地质条件等影响,研究台址周边场地特性必须扣除振动源、振动传播路径及观测仪器的影响。鉴于强震仪幅频较宽的特性,观测仪影响在研究中可以直接剔除,因此,研究中只需剔除振动源与振动传播路径的影响即可(张红才等,2015)。
2.1 H/V谱比法利用台站波形记录研究场地特性,Nakamura于1989年提出H/V谱比法,该方法的理论立足点在于台站波形记录中面波占据相当大的成分,且场地放大效应主要由覆盖于弹性半空间上的软弱土层引起。基本原理为:设VS、VB分别为地表和基底垂直向地震动振幅谱,HS、HB分别为地表和基底水平向地震动振幅谱,则经验传递函数可以表示为
| $ S = {H_{\rm{S}}}/{H_{\rm{B}}} $ | (1) |
实验证明:基底处地震动的垂直分量与水平分量大致相等;垂直分量的土层放大效应远小于水平分量。假定垂直分量基本未被放大,则HB≈VB≈VS,由此,经验传递函数可简化为H/V谱比,即
| $ S = {H_{\rm{S}}}/{V_{\rm{S}}} $ | (2) |
观测台站记录的水平向与垂直向地震动振幅谱之比,即为各观测台站的场地响应(朱荣欢等,2007;徐嘉隽等,2014;张红才等,2015)。
2.2 地脉动谱比值计算利用快速傅里叶变换计算所选地脉动数据,垂直分量采用地表垂直向地震动振幅谱,水平分量的傅里叶谱HS采用NS和EW向的合成谱,即
| $ {H_{\rm{S}}} = \sqrt {H_{{\rm{EW}}}^2 + H_{{\rm{NS}}}^2} $ | (3) |
式中:HEW为地表EW向振幅谱,HNS为地表NS向振幅谱。
依据式(2)计算得到原始H/V谱比,使用Konno K等(1998)提出的平滑方法对振幅谱进行平滑,最终求得平滑后地脉动的谱比值(徐嘉隽等,2014;张红才等,2015)。平滑公式为
| $ {W_{\rm{B}}}\left({f, {f_{\rm{c}}}} \right) = {\left[ {\sin \left({{{\log }_{10}}{{\left({f/{f_{\rm{c}}}} \right)}^b}} \right)/{{\log }_{10}}{{\left({f/{f_{\rm{c}}}} \right)}^b}} \right]^4} $ | (4) |
式中:WB( f,fc)为各中心频率在频域范围内平滑权函数;b为频带宽度系数,本研究中采用b =10;fc为中心频率;f为频率。
2.3 强震动记录谱比值计算由于傅里叶谱尖峰较多且需要进行平滑处理,为了避免计算过程中引入主观误差,Zhao J X等(2006)提出计算单自由度体系阻尼比为5%的水平向与垂直向速度反应谱谱比值来替代傅里叶谱比值。即,假定阻尼比为5%,单条强震动记录的水平分量反应谱采用NS向与EW向反应谱的合成谱,则
| $ P\left(f \right) = \frac{2}{{N\Delta t}}{\left| {Y\left(f \right)} \right|^2} $ | (5) |
依据式(2)计算单条记录的谱比值,最终取平均求得强震动记录的谱比值(冀昆等,2014)。
2.4 数据处理及分析安徽省有7个国家强震动台站采用实时传输模式进行观测,另外2个强震动台站采用事件触发模式进行观测。在本研究中,对7个采用实时传输模式观测的强震动台站进行地脉动谱比值计算。
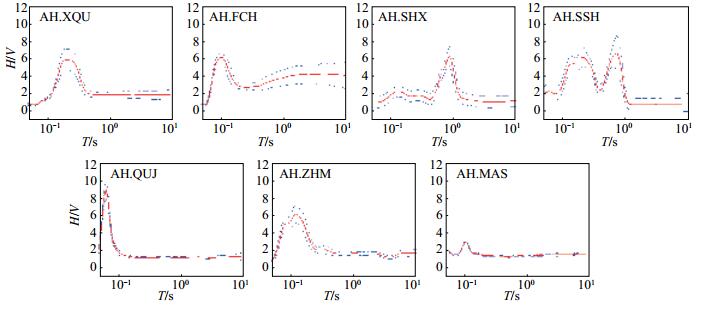
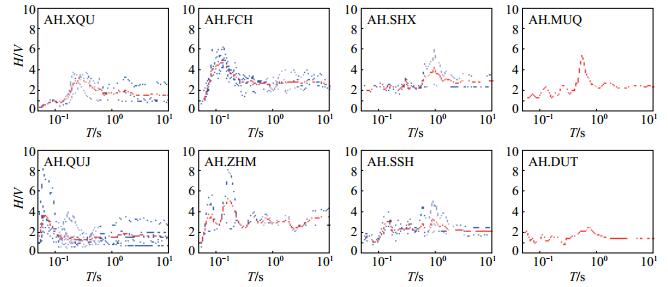
随机选取2016年9月25日强震动记录波形作为原始数据。首先,对预处理后的波形数据按照50%的重叠率进行分段处理,每个波形数据段长度为600 s;然后,依次计算各组波形数据的谱比值,对各组谱比值曲线进行均值化处理,得到台站地脉动谱比值曲线,结果见图 2。收集安徽省国家强震动台站所有历史地震记录,地震目录见表 2。依据阻尼比5%的反应谱,计算各条地震记录强震动台站谱比值曲线,计算结果见图 3。
|
图 2 安徽省国家强震台地脉动谱比值 Fig.2 The spectral ration of the earth pulsation of China strong motion stations in Anhui Province |
| 表 2 安徽省国家强震台历史地震记录 Tab.2 The seismic data of China strong motion stations in Anhui Province |
|
图 3 安徽省国家强震台历史地震谱比值 Fig.3 The spectral ration of the seismic data of China strong motion stations in Anhui Province |
参考强震动台站的场地类型,对比分析强震动台站的地脉动谱比值曲线与历史地震谱比值曲线,可以得到以下结论。
(1)在采用实时传输模式观测的国家强震动台站中,三山台(AH.SSH)谱比值曲线呈现明显的双峰值现象,其他台站均为单峰值曲线;台站谱比值均大于1;周期T > 1 s的谱比值曲线相对平坦;基岩台基的马鞍山台(AH.MAS)谱比值曲线峰值最小。
(2)在利用历史地震记录得出的谱比值曲线中,三山台(AH.SSH)与当涂台(AH.DTU)谱比值曲线呈平坦分布,其他台站的谱比值曲线呈单峰值分布;从沈巷台(AH.SHX)谱比值曲线可以得知,同一台站采用相同观测系统所记录的各条历史地震波形,其反应谱谱比值曲线存在较大差异。
(3)繁昌台(AH.FCH)、香泉台(AH.XQU)、全椒台(AH.QUJ)、沈巷台(AH.SHX)和钟鸣台(AH.ZHM)的各2组谱比值曲线变化趋势保持一致;三山台(AH.SSH)的2组谱比值曲线相差较大;覆盖层最薄的全椒台(AH.QUJ)在平坦区域内(T > 0.1 s)的2组谱比值最接近。
依据图 2与图 3的计算结果,最终得到部分强震动台站的场地卓越周期,结果见表 3。
| 表 3 安徽省部分国家强震台站卓越周期 Tab.3 The predominant period of China strong motion stations in Anhui Province |
由震源发出的有限持续时间瞬时地震信号在频率域可以由振幅谱密度与相位谱等价表示,而环境背景噪声是由各种空间分布,通常互不相关的连续振动源产生,是一种平稳的随机过程,通常采用功率谱密度PSD(Power Spectral Density)来反映地震噪声水平的高低。
3.1 功率谱概率密度函数使用概率密度函数方法估算地震噪声加速度PSD,需要计算每个记录段的加速度PSD值,使用某一倍频程的频率间隔对PSD曲线进行平滑,计算PSD值落在某一个频点某一功率内的记录段数目,以该记录段与总记录段数目的比值作为该频点该功率谱的PSD概率密度函数的取值(廖诗荣等,2008;McNamara D E et al,2009)。
(1)数据预处理。将噪声测试原始速度连续波形记录按照50%的叠加率进行分段,每个记录段长度为600 s。依据观测系统灵敏度,将原始速度连续波形记录转换为相应加速度值;为减少长周期功率谱估计的偏差,对波形数据进行去均值、去长周期成分处理;为减少有限长度数据序列进行FFT变换时造成的频率渗漏,对各段波形数据进行正弦—余弦窗函数滤波。
(2)加速度功率谱密度估算。通过傅里叶变换法计算有限长度数据序列PSD值,即
| $ Y\left(f \right) = \Delta t\sum\limits_{n = 0}^{N - 1} {y\left({n\Delta t} \right){e^{ - i2{\rm{ \mathsf{ π} }}fn\Delta t}}} $ | (6) |
式中:f = k/NΔt,其中k = 0, 1, ..., N-1;N为采用点个数;Δt为采用时间间隔。鉴于地球标准低噪声模型(ALNM)与高噪声模型(AHNM)(Cauzzi C et al,2013),中文PSD表示为总功率谱密度的形式,即
| $ P\left(f \right) = \frac{2}{{N\Delta t}}{\left| {Y\left(f \right)} \right|^2} $ | (7) |
式中:f = k/NΔt,其中k = 0, 1, ..., N/2。
(3)PSD概率密度函数。在0.01—80 Hz频带范围内,对PSD值进行1/3倍频程积分,中心频率fc以1/9倍频程为步长,计算得出fc频点处的PSDa(fc)。
每个中心频率fc的PSD概率密度函数可以表示为
| $ {P_{{\rm{PSD}}}}\left({{f_{\rm{c}}}} \right) = {N_{{\rm{P}}{f_{\rm{c}}}}}/{N_{{f_{\rm{c}}}}} $ | (8) |
式中:Nfc为记录段总数;NPfc为频点fc的PSD取值落在某一PSD窗内的记录段个数,在本研究中PSD窗长与步长取,变化范围为-260—20 dB。
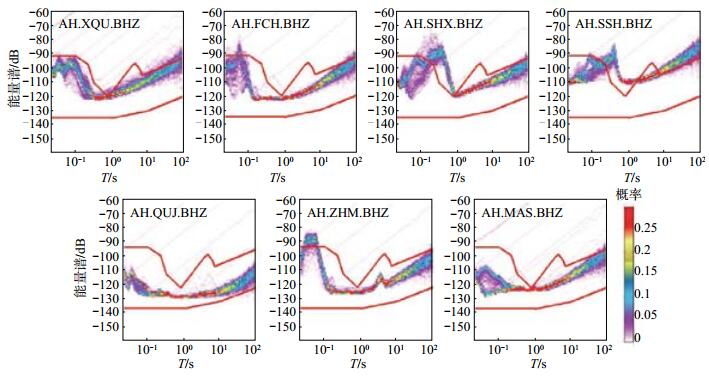
3.2 台站地脉动选取及处理选取相同时间段的波形数据作为原始数据,依据上述步骤对垂直向地脉动数据进行分析处理,结果见图 4。鉴于工程地震学常用的频带范围,文中利用1—20 Hz的加速度均方根振幅RMS描述各强震动台站的背景噪声水平,结果见表 4。
|
图 4 安徽省国家强震台台站背景噪声功率谱概率密度函数值 Fig.4 The probability density functions of the earth pulsation of China strong motion stations in Anhui Province |
| 表 4 安徽省强震动台站背景噪声均方根振幅 Tab.4 The RMS of the earth pulsation of China strong motion stations in Anhui Province |
据图 4和表 4中各强震动台站地脉动功率谱概率密度函数曲线和均方根振幅加速度值,将安徽省采用实时传输模式观测的国家强震动台站分为3类。
(1)均方根振幅加速度值RMS < 2.0×10-6 m·s-2,最大概率密度函数曲线近似为二折线,且绝大部分曲线位于AHNM与ALNM范围内,如:全椒台(AH.QUJ)、马鞍山台(AH.MAS)。
(2)均方根振幅加速度值2.0×10-6 m·s-2 < RMS < 1.5×10-5 m·s-2,最大概率密度函数曲线近似为三折线,且绝大部分曲线位于AHNM与ALNM范围内,如:香泉台(AH.XQU)、全椒台(AH.QUJ)和钟鸣台(AH.ZHM)。
(3)均方根振幅加速度值RMS > 1.5×10-5 m·s-2,且最大概率密度函数曲线在0.1 s < T < 1 s内大部分超出AHNM与ALNM范围,如:沈巷台(AH. SHX)、三山台(AH. SSH)。
4 结论针对安徽省9个国家强震动台站,依据记录的地脉动数据和历史地震数据,对台站的场地响应和背景噪声进行对比分析处理,可知:场地响应曲线呈直线型,且H/V比值为1.5—2的强震动台站,其背景噪声均方根振幅均满足RMS < 2.0×10-6m·s-2;场地响应曲线表现为明显的双峰曲线的强震动台站,其背景噪声均方根振幅均满足RMS > 1.5×10-5 m·s-2;场地响应曲线表现为明显的单峰曲线的强震动台站,其背景噪声均方根振幅变化范围较广。
为了进一步确定强震动台站的场地响应曲线与加速度均方根振幅之间的关系,有待于对大量台基类型已明确的台站进行加速度均方根振幅计算,以获取两者之间的关系。
| 冀昆, 温瑞智, 任叶飞, 王宏伟. 基于芦山余震强震动记录的场地特征分析[J]. 地震工程与工程振动, 2014, 34(5): 35-42. | |
| 廖诗荣, 陈绯雯. 应用概率密度函数方法自动处理地震台站勘选测试数据[J]. 华南地震, 2008, 28(4): 82-92. | |
| 徐嘉隽, 杨贵, 陈家樑, 林家宝. 运用谱比法计算福建地区观测台网台站响应[J]. 震灾防御技术, 2014, 9(Z1): 695-701. | |
| 张红才, 徐嘉隽, 陈智勇. 基于噪声谱比法的福建台网观测台站的场地响应研究[J]. 地震学报, 2015, 37(6): 1045-1058. DOI:10.11939/jass.2015.06.014 | |
| 朱荣欢, 苏有锦. 用H/V谱比法计算云南区域数字地震台站的场地响应[J]. 地震研究, 2007, 30(3): 248-252. | |
| 赵希磊, 张学应, 赵建和, 李发. 安徽强震动台站场地响应研究[J]. 高原地震, 2014, 26(2): 7-11. | |
| Cauzzic C, Clinton J. A High and Low-Noise Model for High-Quality Strong Motion Accelerometer Stations[J]. Earthquake Spectra, 2013, 29(1): 85-102. DOI:10.1193/1.4000107 | |
| McNamara D E, Hutt C R, Gee L S, Benz H M, Buland R P. A Method to Establish Seismic Noise Baselines for Automated Station Assessment[J]. Seismological Research Letters, 2009, 80(4): 628-637. DOI:10.1785/gssrl.80.4.628 | |
| Konno K, Ohmachi T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor[J]. Bulletin of the Seismological Society of America, 1998, 88(1): 228-241. | |
| Zhao J X, Irikura K, Zhang J, et al. An empirical site-classification method for strong-motion stations in Japan using H/V response spectral ratio[J]. Bulletin of the Seismological Society of America, 2006, 96(3): 914-925. DOI:10.1785/0120050124 |
 2018, Vol. 39
2018, Vol. 39
