据中国地震台网测定,北京时间2016年1月21日1时13分在青海省海北藏族自治州门源回族自治县(37.68°N,101.62°E)发生MS 6.4地震。截至2016年12月31日,青海区域地震台网共记录2 072次余震,余震主要集中在主震后10天内发生,而最大余震在主震半年后发生,为2016年8月13日门源ML 5.0地震。
门源地震序列属于主余型地震,震中位于青藏高原东北缘祁连山中东段冷龙岭断裂。祁连山中东段作为青藏高原东北缘的边界带,是中国构造活动和地震活动最强烈的地区之一,存在一系列全新世活动断裂,如昌马-俄博断裂、冷龙岭断裂、托莱山断裂等,曾发生1927年古浪8.0级、1986年门源6.4级等地震。该地震发生在年度重点监视区,近年来随着固定地震台站的加密及科学台阵数据的应用,该地区地震监测能力较好,有必要利用数字地震波形对门源6.4级地震序列进一步分析。
由地震资料可以得到关于应力大小的某种有物理意义的估计,即视应力(Wyss M et al,1968),是一个与震源动力学过程相关的量,为震源的动力学参数。对一个地区中引起地震滑动的视应力水平进行的区域平均,可作为当地绝对应力水平的间接估计(吴忠良等,2001)。视应力可以反映区域应力场的强弱,一般视应力越高,应力水平就越高,反之应力水平则低(陈学忠等,2003)。近年来,视应力在地震预测预报中有了很多应用,如:陈学忠等(2007)探讨了地震视应力用于震后趋势快速判定的可能性,并对河北文安MS 5.1等地震发生前后震源区及附近视应力变化进行研究;李艳娥等(2007)对1999年岫岩5.4级地震序列震源参数测定及标度关系进行了分析,华卫等(2009)分析研究了2008年汶川8.0级地震序列震源参数的分段特征,对强余震与震源参数的时空关系进行了探讨;李国佑等(2015)对比了2008年、2009年大柴旦2次6级地震视应力特征。国内还有很多学者(钱晓东等,2007;杨志高等,2009)探讨研究了视应力在地震预测中的应用。为了研究2016年门源6.4级地震发生前后区域应力场变化,本文对震中附近区域2010年1月至2016年12月ML≥2.5地震及门源6.4级地震序列ML≥2.0地震的震源参数进行计算,分析视应力时空变化特征,总结门源6.4级地震序列前后区域应力场变化。
1 震源动力学参数计算方法根据视应力(σapp)定义
| $ {\sigma _{{\rm{app}}}} = \mu \frac{{{E_{\rm{S}}}}}{{{M_0}}} $ | (1) |
式中,ES为地震辐射能量,M0为地震矩,μ为剪切能量(对于地壳介质,μ = 3×104 MPa)。由式(1)可知,计算地震视应力需计算地震波辐射能量和地震矩,可通过对数字地震波形资料进行震源谱反演分析得到。具体计算步骤可参考陈学忠等(2007)的结果。
中小地震震源谱符合Brune圆盘模型,震源谱可表示为
| $ \mathit{\Omega }\left(f \right) = \frac{\mathit{\Omega }}{{1 + \frac{f}{{{f_{\rm{c}}}}}}} $ | (2) |
式中,Ω0为震源谱零频极限值,fc为拐角频率。当Ω0和fc给定时,式(2)即可确定。因此,确定Ω0和fc就成为震源谱计算的主要内容。地震矩M0可以根据式(3)求得
| $ {M_0} = \frac{{4\pi {v^3}\mathit{\Omega }d}}{R} $ | (3) |
式中,v为波速(P波取6.1 km/s,S波取3.5 km/s),d为震源距,Ω0为震源谱零频极限值,R为辐射因子。
本文所用的地震波形资料均为速度记录,三分向速度记录变换到频率域,利用式(4)可得到速度谱v(f),即
| $ v\left(f \right) = \sqrt {v\left(f \right)_{\rm{Z}}^2 + v\left(f \right)_{{\rm{NS}}}^2 + v\left(f \right)_{{\rm{EW}}}^2} $ | (4) |
地震能量ES可由对速度谱的平方积分求得,即
| $ {E_{\rm{S}}} = 8\pi \rho \beta \int_0^\infty {v{{\left(f \right)}^2}{\rm{d}}f} $ | (5) |
由于地震计频带宽度的有限性,在计算过程中考虑低频和高频补偿,即
| $ {E_{\rm{S}}} = 8\pi \rho \beta \left\{ {\frac{1}{3}{{\left[ {2\pi {f_1}{\mathit{\Omega }_0}} \right]}^2}{f_1} + \int_{{f_1}}^{{f_2}} {v{{\left(f \right)}^2} + {{\left[ {2\pi {f_3}\mathit{\Omega }\left({{f_3}} \right)} \right]}^2}{f_3}} } \right\} $ | (6) |
式中,Ω0为零频极限,β为S波速度,f1、f3分别为拟合震源谱过程中选择的最低频率和最高频率值,中小地震振幅谱符合Brune模型,低频段为水平段,高频段为衰减段,计算过程中f1和f2根据实际情况在振幅谱的平坦部分选择,而f3选在振幅谱衰减段。Ω0(f)对应频率f3的振幅值,可由将Ω0、fc和f3代入式(2)计算的理论值代替。由于地震能量由S波携带,本文主要计算S波的地震能量。
对于某次地震,通常会有多个台站的观测波形资料,据上述方法可分别求得每个台站的震源动力学参数,再求取平均值得到最后的结果。为了消除个别台站的异常高值对平均值的影响,在由各个台站的值求平均时采用Archuleta R J等(1982)的方法,即
| $ \bar x{\rm{ = exp}}\left({\frac{1}{N}\sum\limits_{i = 1}^N {\ln \;{x_i}} } \right) $ | (7) |
| $ \Delta x = \exp \left({\sqrt {\frac{1}{{N - 1}}{{\sum\limits_{i = 1}^N {\left[ {\ln \;{x_i} - \ln \;\bar x} \right]}^2 }}} } \right) $ | (8) |
式中,xi为各台站的地震矩或地震能量;N为台站数;Δx为误差因子,其意义为当x以对数坐标作图时的标准差。
2 数据资料利用青海区域地震台网数字地震波资料,计算2010年1月至2016年12月共184个ML≥2.5地震及2016年1月21日至2016年12月31日门源6.4级序列共150个ML≥2地震的震源动力学参数。计算时选取震中150 km范围内地震台站信噪比较高的记录,对这些数据进行去倾和仪器响应校正处理。图 1给出所选取地震的震中、台站分布及区域地质构造。
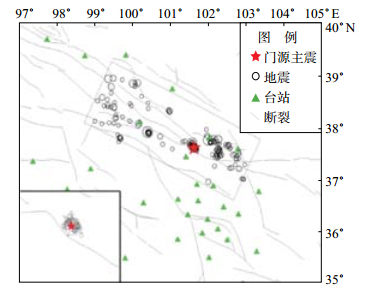
|
图 1 研究区域2010—2016年地震及台站分布 Fig.1 Distribution of earthquakes and stations in the research area from 2010 to 2016 |
利用青海区域台网数字地震波资料,计算研究区内2010-2016年184个ML≥2.5地震的震源动力学参数,见图 2,给出地震矩、地震辐射能量、拐角频率及视应力与震级的关系。

|
图 2 研究区震源动力学参数与震级的定标关系 Fig.2 The scaling relationship between the seismic source dynamics parameter and the magnitude in the study area |
经计算,得到研究区视应力分布在5×102-1.57×106 Pa。本序列得到的地震矩、地震辐射能量、拐角频率及视应力与震级存在以下关系。
| $ \left(1 \right){\rm{地震矩与震级}}\;\;\;\lg {M_0} = 10.71103 + 1.08207{M_{\rm{L}}} $ | (9) |
| $ \left(2 \right){\rm{辐射能量与震级}}\;\;\;\lg {E_{\rm{S}}} = 2.35221 + \begin{array}{*{20}{l}} {1.82262} \end{array}{M_{\rm{L}}} $ | (10) |
| $ \left(3 \right){\rm{拐角频率与震级}}\;\;\;\lg {f_{\rm{c}}} = \begin{array}{*{20}{l}} {0.54632} \end{array} - \begin{array}{*{20}{l}} {0.11385} \end{array}{M_{\rm{L}}} $ | (11) |
| $ \left(4 \right){\rm{视应力与震级}}\;\;\;\lg {\sigma _{{\rm{app}}}} = \begin{array}{*{20}{l}} {2.18939} \end{array}{\rm{ + }}\begin{array}{*{20}{l}} {0.71553} \end{array}{M_{\rm{L}}} $ | (12) |
由图 2及拟合关系式(9)-(12)可以看出,地震矩、地震辐射能量与震级存在较好的正相关系;拐角频率、视应力与震级也具有较明显的相关性,拐角频率随震级增大而减小,视应力随震级增大而增大。
3.2 研究区视应力变化特征2016年门源6.4级地震发生在甘青交界的青海境内(图 1),据发震断层走向和地震台站分布,选取震中附近的矩形区域为研究区。青海区域地震台网对该区ML≥3.0地震有较完整记录。图 3给出研究区2010-2016年ML≥3.0地震的M-T关系、视应力及拐角频率随时间变化关系曲线。

|
图 3 研究区ML ≥ 3地震M—T、视应力及拐角频率随时间的变化关系 Fig.3 The change with time of M—T, apparent stress and corner frequency of earthquakes in the research area |
从M-T图可以发现,该时段内依次发生2012年5月11日甘肃肃南4.9级地震、2013年9月20日青海门源5.1级、2015年11月23日祁连5.2级及2016年1月21日门源6.4级等显著地震事件。在2015年11月23日祁连地震发生前,研究区域存在约1年的ML 3地震平静期,祁连5.2级地震将平静打破后2个月发生门源6.4级地震。对视应力、拐角频率进行对比分析,由视应力随时间的变化曲线发现,几次较大地震对应的视应力明显偏高,视应力存在起伏变化,但异常不明显。由拐角频率随时间变化的曲线发现,2011-2015年存在数次高频地震事件,ML 3地震平静后发生的地震,拐角频率较之前起伏较小,在一定程度上反映了区域应力存在积累-地震平静-发震的过程。
从震源动力学参数与震级之间的定标关系可知,震级与视应力存在明显的正相关性。为了尽可能去除震级对视应力的影响,统计ML 3.0-3.9和ML 2.5-2.9震级段视应力随时间的变化关系。如图 4所示:①ML 3.0-3.9震级段的视应力从2010年底至2012年底存在明显逐步上升过程,之后视应力降低,发生2012年肃南4.9级和2013年门源5.1级地震,2014年小的起伏之后进入ML 3地震平静期,之后发生2015年祁连5.2级和2016年门源6.4级地震;②ML 2.5-2.9震级段的视应力在2010-2012年较低,2012-2015年初存在明显起伏变化,并在此变化过程中发生祁连和门源地震。
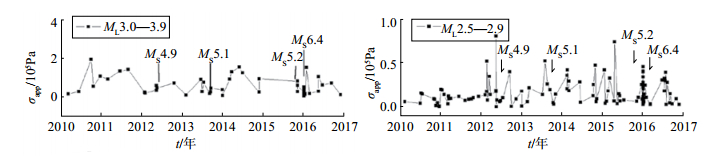
|
图 4 研究区域ML 3.0—3.9、ML 2.5—2.9地震视应力随时间的变化 Fig.4 The change with time of apparent stress of ML 3.0—3.9 and ML 2.5—2.9 earthquakes in the research area |
为了进一步分析门源6.4级地震前视应力空间分布,将门源6.4级地震前研究区ML 3.0-3.9和ML 2.5-2.9震级段的视应力分别减去该时段视应力的平均值,对该视应力与平均值的差值按照0.01°×0.01°进行网格化,绘制视应力空间分布,见图 5。由图 5可见:①ML 3.0-3.9视应力差值主要分布在-0.05 MPa-0.05 MPa,门源地震发生在视应力高低交界区域;②ML 2.5-2.9视应力差值主要分布在-0.02 MPa-0.02 MPa,门源地震发生在视应力高值区域,离门源地震约30 km的昌马-俄博断裂附近发生的小震视应力相对偏高。

|
图 5 门源6.4级地震前ML 3.0—3.9和ML 2.5—2.9震级段地震视应力空间分布 Fig.5 Spatial distribution of apparent stress of ML 3.0—3.9 and ML 2.5—2.9 earthquakes before Menyuan MS 6.4 in the research area |
门源6.4级地震的视应力为1.57 MPa,该值高于吴忠良等(2002)给出的中国大陆地震的视应力平均值(0.8 MPa),但与青藏高原东北缘平均视应力高于其邻近地区的结论是一致的。下面进一步探讨门源地震序列ML 5.0强余震前小震视应力变化特征。为了消除震级对视应力的影响,以ML 2.0-2.5和ML 2.6-3.0震级段讨论地震视应力随时间的变化。
如图 6所示,2016年1月21日门源序列ML 2.0-2.5震级段余震视应力在3月1日之前较高,随后降低,6月开始逐渐升高,在此过程中发生2016年8月13日发生ML 5.0地震,随后发生的余震视应力逐渐降低。ML 2.6-3.0震级段的地震呈现相似变化,主震发生后短时间内发生的余震视应力较高,随着时间的推移视应力逐渐降低,8月3日发生的ML 2.9、ML 2.7地震与8月9日发生的ML 2.9地震视应力相对较高,几次小地震可能与门源ML 5.0地震的发生有一定关系。对2个震级段地震视应力分析可知,门源地震序列视应力表现出以下特征:主震后短时间内发生的余震视应力较高,且随时间逐渐降低,而ML 5.0强余震发生前,小震视应力出现升高变化。视应力的变化可能反映了震源区应力的增强。

|
图 6 2016年门源地震序列ML 2.0—2.5和ML 2.6—3.0震级段视应力随时间变化 Fig.6 The change with time of apparent stress of ML 2.0—2.5 and ML 2.6—3.0 Menyuan earthquakes in 2016 |
通过对门源6.4级地震周边区域2010-2016年ML≥2.5地震及门源地震序列ML≥2.0地震的震源参数计算,得出以下结论。
(1)通过对地震序列震源参数与震级的定标关系进行分析,发现地震矩、地震辐射能量与震级存在较好的正相关性;拐角频率、视应力与震级存在较明显的相关性,拐角频率随震级增大而减小,视应力随震级增大而增大。
(2)研究区域在门源地震前存在约1年的ML 3地震平静,ML≥3.0地震拐角频率在地震平静之前起伏变化明显,门源地震后变化减小。研究区域ML 3.0-3.9和ML 2.5-2.9震级段地震视应力在门源地震前存在不同程度的起伏变化,反映了门源地震前区域应力场的增强。
(3)门源6.4级地震序列ML 2.0-2.5和ML 2.6-3.0震级段视应力表现出主震后短时间内发生的余震视应力较高、随时间逐渐降低的特点,但发生ML 5.0强余震前,小震视应力呈现了升高的变化过程,可能反映了震源区应力的增强。
感谢中国地震局地球物理研究所李艳娥副研究员就程序使用给予的指导。
| 陈学忠, 李艳娥. 2006年7月4日河北文安MS 5.1地震前震中周围地区小震视应力随时间的变化[J]. 中国地震, 2007, 23(4): 327-336. | |
| 陈学忠, 王小平, 王林瑛, 等. 地震视应力用于震后趋势快速判定的可能性[J]. 国际地震动态, 2003(7): 1-4. | |
| 华卫, 陈章立, 郑斯华. 2008年汶川8.0级地震序列震源参数分段特征的研究[J]. 地球物理学报, 2009, 52(2): 365-371. | |
| 李国佑, 姚家骏. 2008年、2009年大柴旦两次6级地震序列地震视应力特征[J]. 地震地磁观测与研究, 2015, 36(3): 53-57. | |
| 李艳娥, 陈学忠. 1999年11月29日岫岩5.4级地震序列震源参数测定及标度关系分析[J]. 地震, 2007, 27(4): 59-67. | |
| 钱晓东, 李琼, 秦嘉政. 2007年宁洱6.4级地震序列视应力研究[J]. 地震研究, 2007, 30(4): 311-317. | |
| 吴忠良. 由宽频带辐射能量目录和地震矩目录给出的视应力及其地震学意义[J]. 中国地震, 2001, 17(1): 8-15. | |
| 吴忠良, 黄静, 林碧苍. 中国西部地震视应力的空间分布[J]. 地震学报, 2002, 24(3): 293-301. | |
| 杨志高, 张晓东. 首都圈地区地震视应力的计算及空间分布[J]. 地震, 2009, 29(4): 32-43. | |
| Archuleta R J, Cranswick E, Mueller C, et al. Source parameters of the 1980 Mammoth Lakes, California, earthquake sequence[J]. J Geophys Res, 1982, 87(B6): 4595-4607. DOI:10.1029/JB087iB06p04595 | |
| Wyss M, Brune J N. Seismic moment, stress, and source dimensions for earthquakes in the California Nevada Region[J]. J Geophys Res, 1968, 73(14): 4681-4694. DOI:10.1029/JB073i014p04681 |
 2018, Vol. 39
2018, Vol. 39