2. 中国合肥 230026 中国科学技术大学
2. University of Science and Techonlogy of China, Hefei 230026, China
地震定位指的是,根据地震观测台站对地震到时的观测,确定震源位置以及发震时刻。地震定位作为地震监测与减灾研究的重要基础,对于研究如地震活动构造、地球内部结构、震源几何构造等地震学的基本问题有重要意义。此外,基于快速准确的地震定位的地震速报,对于震后的减灾、救灾工作也是至关重要的(田玥等,2002)。
大陆地震指的是震中位于大陆地壳内的地震,简称陆震。与海震不同的是,陆震激发的横波、纵波最终能够传播到地表,故震级相当的陆震破坏性一般大于海震;加之陆震多为浅源地震,板内地震大多集中在5—35 km的深度,下地壳极少甚至没有地震发生(罗文行等,2008)。对于一般的浅源地震,由于震源位置离地表较近,震级较小时也会对地面建筑物以及生命财产安全造成不可估量的损失,所以通过一定方法准确确定大陆地震的三要素(发震时刻、震中和震级),对震后灾害评估具有重要作用。
本文基于大陆地震的传播方式及相关原理,通过模拟退火法反演大陆地震的发震位置,对于在地壳中传播的浅源地震忽略介质差异对传播速度的影响。
1 模拟退火法简介模拟退火算法(Simulated Annealing,SA)是一种非线性反演,能够避免使反演陷入失配函数的次极小,或者模型的后验概率密度分布函数的次极大,或称局部极大值而不是全局最大值。模拟退火实质是现代蒙特卡洛法,是一个不断寻优过程,在此过程中,拟合度随迭代次数的增加呈现跳跃起伏,但总体趋势是变大或变小,正是由于模拟退火允许拟合度变小或拟合误差变大,从而使模型从局部最优值中跳出,得到全局最优化模型(师学明等,2007)。
模拟退火法步骤如下:①给定模型每一个参数变化范围,随机选择一个初始模型m0,并计算相应的目标函数值E(m0);②对当前模型进行扰动产生一个新模型m,计算相应的目标函数值E(m),得到ΔE = E(m)-E(m0);③若ΔE<0,则新模型m被接受,若ΔE>0,则新模型m按概率P = exp(-ΔE/kT)进行接受,其中k是一个常数,exp表示自然指数,T为温度。因为P(ΔE)的函数取值范围是(0,1),在0—1之间随机产生一个数R,当P(ΔE)>R时,接受修改,即m0 = m。公式表明:温度越高,出现一次能量差为dE的降温概率越大;温度越低,则出现降温的概率越小;④在温度T下,重复一定次数的扰动和接受过程,即重复步骤②、③;⑤缓慢降低温度T,Tnew = 0.98×n×T;⑥重复步骤②—⑤,直至满足收敛条件为止。为了避免最好的解在优化过程中被忽略掉,可以在整个搜索过程中随时记下最好的值,因为该算法的特性决定了当收敛条件设置过大时,随着迭代次数的增加可能跳出全局最优解而到达局部最优解,此时可以通过记录排除伪最优解(段红伟等,2007)。
2 实验模拟 2.1 建立模型假设震源三维坐标为(x0,y0,h0),其中(x0,y0)为震源投影到地球上的平面坐标,h0为震源深度,发震时刻为xx年xx月xx日x时x分x秒,地震波传播速度设为v,单位为km/s。用(xi,yi),其中i = 1,2,3,…,n,分别表示n个接收到地震波台站的平面坐标,用Δti表示地震到第i个台站的走时,单位为秒。根据以上条件可以建立以下非线性模型
| $ \Delta {t_i} = \frac{{\sqrt {{{\left({{x_i} - {x_0}} \right)}^2} + {{\left({{y_i} - {y_0}} \right)}^2} + h_0^2} }}{v} $ | (1) |
其中,x0、y0、h0为震源参数。
2.2 数据准备以2016年12月18日11时08分50秒山西清徐M 4.1地震和2016年3月12日11时14分10秒山西盐湖M 4.3地震为例,其相应震源参数见表 1。依据华北西部10 km深度P波速度结构等值线图,得到v = 6.03—6.33 km/s;华北西部20 km深度P波速度结构等值线图,得到v = 6.2—6.48 km/s(魏文博等,2007)。将震源经纬度通过高斯投影正算转换成平面坐标,再以10个地震台站接收的地震实际走时进行反演计算,将反演得到的震源坐标通过高斯投影反算,转化为经纬度,并与实际震源位置作比较。需要注意的是,实际走时中含有高程误差、速度误差、震相人工读取误差。
| 表 1 地震参数信息 Tab.1 Seismic parameter information |
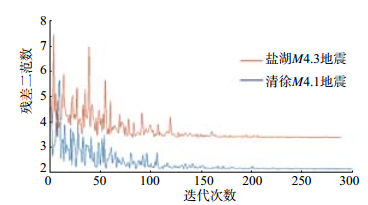
(1)初始温度T = 1时,降温速度T = T×0.98,收敛阈值分别为0.02与0.005,得到反演值与真实值对比结果,见表 2,迭代次数与残差二范数关系曲线见图 1。
| 表 2 真实值与反演值(初始温度T=1) Tab.2 The real data and inverse data(Initial temperature T = 1) |
|
图 1 收敛迭代次数与残差二范数曲线(T = 1) Fig.1 Convergence curve of residual two norm with iteration number (T = 1) |
在本次反演过程中,由于震源参数初始值与真值接近程度不同,决定了收敛速度的不同,为了使2次反演结果均收敛到全局最优,故设定不同的收敛阈值。当目标函数收敛时,反演误差为(0.006 5,0.018 3,8.27)及(0.022 6,0.039 6,4.98),其中纬度、经度误差较小,深度h的误差较大,表明震源深度反演精度较小,残差二范数的值为2.2与3.5,表明高程误差、速度误差、人工读取震相误差对反演结果存在一定影响,主要体现在震源位置与目标函数残差中。
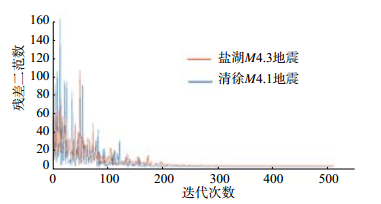
(2)初始温度T = 50,降温速度T = T×0.98,收敛阈值为0.02与0.005,得到反演值与真实值对比结果,见表 3,迭代次数与残差二范数关系曲线见图 2。
| 表 3 真实值与反演值(初始温度T = 50) Tab.3 The real data and inverse data(Initial temperature T = 50) |
|
图 2 收敛迭代次数与残差二范数曲线(T = 50) Fig.2 Convergence curve of residual two norm with iteration number (T = 50) |
在本次反演过程中,当目标函数收敛时,反演结果误差和试验1的大致相同,但迭代次数明显增加,可看出初始温度增大迭代次数变多,反演误差基本没有变化。
(3)初始温度T = 1时,降温速度T = T×0.98,收敛阈值均为0.1,得到反演值与真实值对比结果,见表 4,迭代次数与残差二范数关系曲线见图 3。
| 表 4 真实值与反演值(初始温度T = 1,收敛阈值0.1) Tab.4 The real data and inverse data(Initial temperature T = 1, threshold value 0.1) |

|
图 3 收敛迭代次数与残差二范数曲线(阈值变大) Fig.3 Convergence curve residual two norm with iteration number (the threshold becomes bigger) |
在本次反演过程中,当收敛阈值变大后,迭代结束时反演结果未收敛,反演结果误差较试验1中大,迭代次数变少,说明收敛阈值对反演结果精度和迭代次数均有影响,较大的收敛阈值可能会使反演在未遍历搜索空间的情况下提前终止。
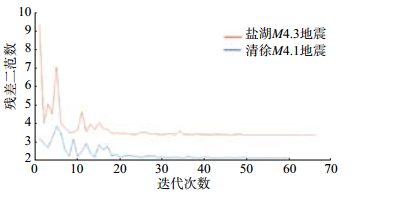
(4)初始温度T = 1时,降温速度由T = T×0.98变为T = T×0.9,收敛阈值分别为0.02与0.005,得到反演值与真实值对比结果,见表 5,迭代次数与残差二范数关系曲线见图 4。
| 表 5 真实值与反演值(初始温度T = 1,降温速度T = T×0.9) Tab.5 The real data and inverse data(Initial temperature T = 1, cooling rate T = T×0.9) |
|
图 4 收敛迭代次数与残差二范数曲线(收敛函数改变) Fig.4 Convergence curve of residual two norm with iteration number (convergence function changes) |
在本次反演过程中,当目标函数收敛时,反演结果误差较试验1中稍微偏大,迭代次数明显变少,可看出,当降温系数变小时,迭代次数明显变少。说明降温系数对反演结果精度有一定影响,对迭代次数影响较大。
3 结论通过对试验结果的综合分析,可以得出以下结论。
(1)设置不同的反演参数会得到不同的反演结果,但即使是全局最优解也存在一定误差。这是由于,在计算地震真实走时时含有高程误差、速度误差、人工读取震相误差,此方法不能很好地消除这些误差。
(2)利用模拟退火法可以反演出较好的地震参数,但在深度上的误差要更大,这是由于经纬度接收的信息路径多,受到的数学约束多,深度只能从一个方向上接收到,受到的数学约束少。
(3)模拟退火法反演震源位置很大程度上依赖于先验模型和实际反演操作经验,当实际操作经验欠缺时,有必要通过设置较大的初始值、较高的降温系数和较小的收敛阈值来进行反演试验,此时往往需要耗费大量的计算时间,但只要参数和初始值取值合理,经过一定时间运算,均能取得比较理想的结果。
| 段红伟, 胡劲松. 基于模拟退火算法的实现及应用[J]. 科技信息(学术版), 2007(31): 544-546. | |
| 罗文行, 李德威, 汪校锋. 青藏高原板内地震震源深度分布规律及其成因[J]. 中国地质大学学报(地球科学), 2008, 33(5): 618-625. | |
| 师学明, 王家映. 地球物理资料非线性反演方法讲座(三):模拟退火法[J]. 工程地球物理学报, 2007, 4(3): 165-174. | |
| 田玥, 陈晓非. 地震定位研究综述[J]. 地球物理学进展, 2002, 17(1): 147-155. | |
| 魏文博, 叶高峰, 金胜. 华北地区P波三维速度结构[J]. 中国地质大学学报(地球科学), 2007, 32(4): 441-452. |
 2018, Vol. 39
2018, Vol. 39
