利用观测到时确定震源位置,已成为现代地震台网的常规任务,但地震定位精度仍然有待提高。传统交切法具有稳健和效率高的优点,但基于均匀或横向均匀介质模型使其定位精度较低(朱元清,1997)。为此,需要对传统的定位交切法进行改进。当使用的地壳速度结构较为复杂时,震源轨迹难以以解析形式表达,为此改进后的方法不求取解析式,而是利用到时约束,将震源定位于总的到时差残差最小处。在使用理论模型验证后,将基于三维复杂地壳速度结构模型的地震定位交切法应用于云南地区,对选取地震进行重定位,得到较为精确的定位结果。
1 方法原理复杂地壳速度模型的地震定位方法(周建超等,2012)借鉴了传统交切法的思想,即利用震源轨迹进行定位。当使用的速度结构较为复杂时,震源轨迹在空间域中以离散方式表示,利用最小走时树射线追踪技术进行计算(赵爱华等,2003)。在传统的交切法中(廉超等,2006),震源轨迹用观测到时差进行约束,以避开发震时间问题(赵爱华等,2004),本文亦采用该做法。
当目标区域地下速度分布已知,在地表有M个地震台站,用Ri(i=1,2,3,…,M)表示。将该地区速度模型离散化,离散成大小相等的立方体单元。在模型小立方体单元内,地震波速度为常数,即介质各向同性。分别在台站Ri(i=1,2,3,…,M)处激发地震,在每个台站激发地震的纵波(P波)和横波(S波),利用最小走时树射线追踪方法,计算丛台站激发的地震波到节点x = (x,y,z)的初至波走时TP(x,Ri)、TS(x,Ri) (i=1,2,3,…,M)。这样,任意2个走时场可构成1个走时差场,则
| $\begin{array}{l} DT\left( {x;{R_{j1}},{W_{j1}};{R_{j2}},{W_{j2}}} \right) = T\left( {x;{R_{j1}},{W_{j1}}} \right) - T\left( {x;{R_{j2}},{W_{j2}}} \right)\\ \left( {j = 1,2,3, \cdots, K} \right) \end{array}$ | (1) |
其中,Rj1和Rj2分别表示对应第j个走时差场的2个走时场的地震台站;Wj1和Wj2和分别表示波的类型,即P或S;K为走时差场数。对于区域内的某个地震,震源在x0 = (x0,y0,z0),发震时间为t0,台站Ri记录到的P波、S波的初至到时分别为τRiP和τRiS,其震源轨迹满足以下方程
| $DT\left( {x;{R_{j1}},{W_{j1}};{R_{j2}},{W_{j2}}} \right) = \tau \mathop {{R_{j1}}}\limits^{{W_{j1}}} - \tau \mathop {{R_{j2}}}\limits^{{W_{j2}}} \quad \left( {j = 1,2,3, \cdots ,K} \right)$ | (2) |
理论上,得到的震源轨迹将交切于一点,即震源点。但实际上,无论是得到的地质模型,还是初至波走时均会或多或少地存在误差,因此震源轨迹很难交于一个点,而是交汇成一个小的区域,该区域大小即反映了地震定位精度。在本文中,将震源定位于轨迹交会最为集中的点x0*=
| $RDT\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{j = 1}^K {\left| {DT\left( {\mathit{\boldsymbol{x}};{R_{j1}},{W_{j1}};{R_{j2}},{W_{j2}}} \right) - I\left( \mathit{\boldsymbol{x}} \right)\left( {\tau \mathop {{R_{j1}}}\limits^{{W_{j1}}} - \tau \mathop {{R_{j2}}}\limits^{{W_{j2}}} } \right)} \right|} $ | (3) |
其中,I(x)=1。x0*点可通过扫描整个模型节点空间找到。
2 改进交切法在云南地区应用 2.1 目标区域选择云南地区位于青藏高原东南缘,受到印度板块向北与欧亚板块正面碰撞的挤压和俯冲,且该地区主应力方向在各时期是不断变化的,因此地质构造格局复杂;研究区域是地震多发地区,有丰富的地震数据资料。在20世纪,云南省共发生5.0级以上地震289次,6.0级以上地震76次。云南地区人民聚居区主要集中在盆地、盆地边缘或附近山谷,因地震震源较浅,震级比较大,常造成较为严重的灾害。如果能有效、快速地给出精确的地震定位,对该地区的防震减灾具有重要意义。
2.2 地壳速度模型建立双台相速度层析成像反演具有较高的分辨率和可靠性,能揭示出与人工地震探深相似的地壳速度结构。何正勤等(2004)根据云南地区基阶瑞利波相速度频散资料,利用面波层析成像方法反演得到目标区域地壳速度结构,给出沿北纬22°—27°方向的速度结构。本研究利用该结论,对已有地壳速度结构进行差值,得到网格节点间隔为5 km的地壳速度模型。5 km、10 km、15 km、20 km深度处的S波地壳速度结构见图 1。

|
图 1 不同深度处地壳速度结构 (a)5 km;(b)10 km;(c)15 km;(d)20 km Fig.1 The velocity models in different depth |
得到地壳速度模型后,将每个地震台站的Ri设定为震源位置并激发地震。利用最小走时树射线追踪方法,分别计算在地震台站Ri激发的P波和S波到每个节点的初至波走时,即TP(x,Ri)、TS(x,Ri),将记录的地震波到每个节点的初至走时作为数据库。对选定区域,在地下构造稳定情况下,此过程只需计算一次,以后每次定位时只需调用,无需重新计算。
2.4 地震重定位选取云南地区2001—2010年4级以上地震,重新标定震相,以期得到更为准确的地震波到时,减小误差。将地震台站任意组成k个台站对,每个台站对对应一个残差场,将k个残差场叠加后搜索所有节点的残差最小值处,即为震源位置。
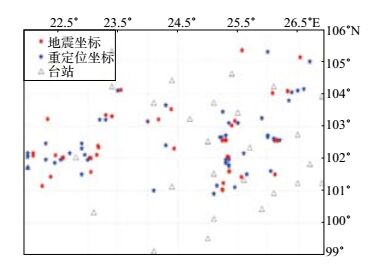
由图 2看出,改进后的地震定位结果与中国地震台网中心定位结果基本一致,可见改进后的地震定位交切法有别于传统交切法。传统交切法因基于均匀或横向均匀介质模型而导致其定位精度较低,而改进后的方法能够适用于复杂地壳速度模型,且地震定位精度较高,误差较小。
|
图 2 地震重定位结果 Fig.2 The result of the earthquake location |
传统的地震定位交切法使用均匀或横向均匀介质模型,假定震源轨迹为球形或者是双曲面。而改进后的交切法不再假定固定的震源轨迹,利用具有良好稳健性的最小走时树射线追踪技术,准确计算所有节点的残差场,在残差场中搜索残差最小的点作为震源点,因而可将交切法用于复杂地壳速度模型下的地震定位。
改进的交切法突破了传统地震定位方法在简单速度模型上的束缚,应用于复杂地壳速度模型,表现出较高的地震定位精度。虽然计算初至波走时比较费时,但在该地区地下速度结构稳定、台站稳定的前提下,将计算信息存入数据库,之后地震定位时直接调用即可,在保持传统定位方法稳健和效率高等优点的基础上,提高了计算效率,可以迅速进行地震定位。
改进的交切法仍存在一些问题,在进行地震定位时需注意,如:①在将该方法应用于云南地区地震定位时,发现在水平方向上定位误差较小,而竖直方向上误差仍较大;②当可用震相较少时,地震定位精度较低。
| 何正勤, 叶太兰, 苏伟. 云南地区地壳中上部横波速度结构研究[J]. 地球物理学报, 2004, 47(5): 838-844. | |
| 廉超, 李胜乐, 董曼, 等. 球面交切法地震定位[J]. 大地测量与地球动力学, 2006, 26(2): 99-103. | |
| 赵爱华, 张中杰, 王光杰, 等. 非均匀介质中地震波走时与射线路径快速计算技术[J]. 地震学报, 2000, 22(2): 151-157. | |
| 赵爱华, 张中杰, 彭苏萍. 复杂地质模型转换波快速射线追踪方法[J]. 中国矿业大学学报, 2003, 32(5): 513-516. | |
| 赵爱华, 张中杰. 三维复杂介质中转换波走时快速计算[J]. 地球物理学报, 2004, 47(4): 702-707. | |
| 周建超, 赵爱华. 三维复杂速度模型的交切法地震定位[J]. 地球物理学报, 2012, 55(10): 3347-3354. DOI:10.6038/j.issn.0001-5733.2012.10.017 | |
| 朱元清, 赵仲和. 提高地震定位精度新方法的研究[J]. 地震地磁观测与研究, 1997, 18(5): 59-67. |
 2017, Vol. 38
2017, Vol. 38