2. 中国杭州 310013 浙江省地震局
2. Zhejiang Earthquake Agency, Hangzhou 310013, China
时频分析是指用时间和频率的联合函数来对信号进行表征与分析(葛学哲等,2006)。时频分析思想始于20世纪40年代,Gabor D(1946)提出Gabor变换,为此后在时间和频率联合域内分析信号奠定了理论基础。Potter R K等(1947)首次提出1种实用的时频分析方法——短时Fourier变换,并将其绝对值的平方称为“声音频谱图”。Ville J(1948)将Wigner在1932年提出的Wigner分布引入信号分析处理领域。20世纪60年代中期,Cohen发现众多时频分布只是Wigner-Ville分布的变形,可以用统一形式表示,习惯称之为Cohen类时频分布(Cohen L, 1989, 1995)。之后,Jones D L等(1995)提出数据自适应最优核时频分布等。这类方法实际上从提高分辨率和抑制交叉干扰项的目的出发。从此,时频分析技术得到长足发展,目前已经广泛应用于通信、自动化、雷达、声纳、生物、天文、医学、地球物理和故障诊断等领域(葛哲学等,2006)。
时频分析在地学中的早期应用主要是对天然地震余震时频特征的研究(Utsu T,1962)、古地磁变化的时频研究(Chant I J et al,1992)以及人工地震信号的除噪及能量补偿的研究等(高军等,1996)。随着时频理论的发展及计算机运算能力的增强,时频特征表示在地学中应用的深度和广度也在不断增加(王培茂,2008)。在地震勘探、数字地震波形研究、地震前兆数据处理及异常提取等方面发挥着重要作用。地震波属于非平稳信号,传统的傅里叶变换因缺乏信号局域性信息而无法对非平衡信号进行全面描述,对此,时频分析是有力的分析工具。
20世纪60年代开始,地球物理学家将时频分析引入地震波形处理,之后在地震勘探领域获得长足发展(刘希强等,2000)。在中国地震预测领域,随着中国地震局“九五”项目的实施,地震波形由图纸改为数字信号记录,数字波形携带大量反映震源、几何扩散、非弹性衰减等方面的信息,同期信号处理技术得到快速发展并完善。在上述背景下,地震学者们从震相识别、人工地震与天然地震区分等不同角度,逐步开展基于时频分析技术的数字地震波应用研究工作,并取得一系列研究成果(许康生,2000;刘希强等, 2003, 2004;陈学华等,2005;张帆等,2006;许朝阳等,2008;姚家骏等,2011)。由于上述研究历史较短,仍处于探索、尝试阶段,并未形成较为成熟和完善的学科体系,因此继续开展相关方研究具有重要意义。
本文作者尝试对数字地震波形进行时频分析,研究其频谱结构及随时间的变化特征,以促进时频分析在测震学中的应用。
1 方法、技术 1.1 时频分析理论时频分析的基本任务是建立1个函数,且要求该函数不仅能够同时用时间和频率描述信号的能量密度,还能够以同样方式用于计算任何密度。时频分析时,一般需满足以下5个特性(张帆,2006;陈斌,2007;刘丽娟,2008;陈友良,2011)。
(1) 时频分析的结果必须是实的。
(2) 由时频分析关于时间t 和频率f的积分可给出信号的总能量E,即
| $\int_{ - \infty }^\infty {\int_{ - \infty }^\infty {p\left( {t,f} \right)} } {\rm{d}}t{\rm{d}}f = E$ | (1) |
(3) 边缘特性,即时频分析关于时间t和频率 f的积分,分别给出信号在频率 f 的谱密度和信号在t时刻的瞬时功率。
| ${\int_{ - \infty }^\infty {p\left( {t,f} \right){\rm{d}}t = \left| {s\left( f \right)} \right|} ^2}\quad \quad {\int_{ - \infty }^\infty {p\left( {t,f} \right){\rm{d}}f = \left| {s\left( f \right)} \right|} ^2}$ | (2) |
(4) 时频分析的一阶矩给出信号的瞬时频率fi(t)和群延迟τg(f),即
| ${f_l}\left( t \right) = \frac{{\int_{ - \infty }^\infty {f \cdot p\left( {t,f} \right){\rm{d}}f} }}{{\int_{ - \infty }^\infty {p\left( {t,f} \right){\rm{d}}f} }}{\rm{和}}{\tau _g}\left( f \right) = \frac{{\int_{ - \infty }^\infty {t \cdot p\left( {t,f} \right){\rm{d}}t} }}{{\int_{ - \infty }^\infty {p\left( {t,f} \right){\rm{d}}f} }}$ | (3) |
(5) 有限支撑特性,从能量角度提出的时频分析基本性质。在信号处理中,为了工程上的近似,往往要求信号具有有限时宽和有限带宽。如果信号s(t)只在某个时间区间取非零值,并且信号的频谱s(f)也只在某个频率区间取非零值,则称信号s(t)及其频谱是有限支撑的。类似的,如果在s(t)和s(f)的总支撑区以外,信号的时频分析结果为零,就称时频分析是有限支撑的。
1.2 数字地震地震波预处理及时频方法选取(1) 数字地震波预处理。2008年后,中国地震观测主要采用数字地震仪系统,产出大量采样率及分辨率较高、记录频带宽、动态范围大的数字化地震波形资料。由于地震观测系统均为动态范围和频率范围有限的选频系统,记录的地面运动存在不同程度的畸变;各种形式的外界干扰和系统内部噪声对地震记录也有一定影响。在记录和传播过程中,会出现倾斜、漂移、波形畸变等现象,在对地震波进行波谱分析前,必须进行扣除仪器响应、去噪等预处理(张帆,2006)。
在此,以2015年4月15日内蒙古阿拉善左旗发生MS 5.8地震为例,对乌海台记录的NS向地震波形进行预处理。内蒙古自治区测震台网提供的数字地震波形资料主要为counts数记录,见图 1(a)。在进行时频分析前,对其进行扣除仪器响应等操作,转为速度记录(本文将地震波速度记录作为时频处理对象)。在此基础上,用数字滤波器,将数字地震波中噪声等成分进行滤除,结果见图 1(b)。

|
图 1 阿拉善左旗MS 5.8地震乌海台NS向波形记录 Fig.1 NS direction seismic waveforms of MS 5.8 Alxa Left Banner earthquake recorded at Wuhai Seismic Station |
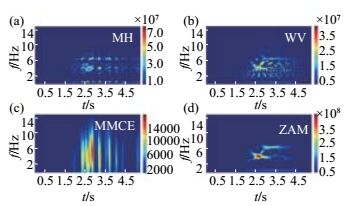
(2) 时频方法选取。常见时频分析方法有线性和非线性时频分析。其中,线性时频包括短时傅里叶变换(STFT)、小波变换(WT)和S变换(ST);非线性时频包括Cohen类双线性时频分布、仿射类双线性时频分布、重排类双线性时频分布、自适应核函数类时频分布、参数化时频分布和局域波时频分析等(张帆,2006)。本文采用乌海台记录到的2010年4月15日内蒙古阿拉善左旗MS 5.8地震EW向P波为研究对象,相继选用BJ、BUD、CW、GRD、MH、MHS、MMCE、PAGE、PMH、PPAGE、PWV、RIDB、RIDH、RIDT、SP、WV、SPWV、ZAM、MSC等方法,进行时频处理,图 2给出部分时频分析方法的处理结果。
|
图 2 阿拉善左旗MS 5.8地震石嘴山台记录波形时频结果 Fig.2 Time-frequency results of seismic waveforms of MS 5.8 Alxa Left Banner earthquake recorded at Wuhai Seismic Station |
由奈奎斯特定理可知,若采样频率为f,则该信号所包含的有效信息频段最大频率可达到f/2(万永革,2012)。本文所采用的数字地震波采样频率均为100 Hz(杨彦明等, 2013, 2016),所得时频结果频段在0—50 Hz,考虑到典型震相等变化信息对应的高能量密度并未分布在整个频段内,而是集中于某一小的频段,因此在绘制时频分布图时,根据实际情况对归一化频率范围进行合理选取,达到所绘制结果既包含有效信息对应的能量密度分布,又可以突出主要变化对应的能量密度分布细节的目的(图 2)。
时频分析具有时间分辨率与频率分辨率相矛盾、高聚集性和低交叉项相矛盾等特点。图 2(a)、图 2(b)显示,采用MH和WV方法进行分析,时频分布结果虽具有较高的分辨率和聚集性,但同时具有很多实际不存在的交叉项;图 2(c)显示,MMCE方法给出的时频结果有效抑制了交叉项,但分辨率降低;由图 2(d)可见,赵—阿特拉斯—马克斯(ZAM)时频分析方法既有效提高了分辨率,又抑制了交叉项的产生。本文从数据自身特征、分辨率、聚集性和交叉性等角度,选取ZAM方法对数字地震波形数据进行时频分析。
2 爆破与天然地震的时频分析结果采用ZAM方法,选取内蒙古自治区1次天然地震及震级相当的1次爆破事件进行时频分析。以2013年7月3日内蒙古阿拉善左旗ML 3.8地震(39.92°N,106.73°E)为例,给出乌海台、石嘴山台数字地震波的时频分析结果,见图 3、图 4。并以2016年6月16日阿拉善左旗ML 3.0爆破(39.15°N,106.11°E)为例,给出乌海台、石嘴山台记录的数字地震波对应的时频结果,见图 5、图 6。表 1给出2次地震事件时频分析的主要参数结果。

|
图 3 阿拉善左旗ML 3.8地震乌海台记录的波形时频结果(震中距30 km) Fig.3 Time-frequency results of seismic waveforms of ML 3.8 Alxa Left Banner earthquake recorded at Wuhai Seismic Station(epicenter distance 30 km) |
|
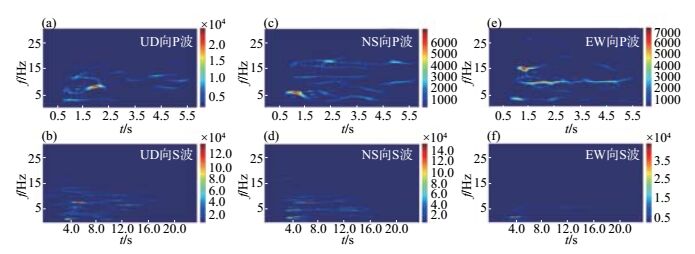
图 4 阿拉善左旗ML 3.8地震石嘴山台记录的波形时频结果(震中距71 km) Fig.4 Time-frequency results of seismic waveforms of ML 3.8 Alxa Left Banner earthquake recorded at Shizuishan Seismic Station(epicenter distance 71 km) |

|
图 5 阿拉善左旗ML 3.0爆破乌海台记录的波形时频结果(震中距85 km) Fig.5 Time-frequency results of seismic waveforms of ML 3.0 Alxa Left Banner blasting recorded at Wuhai Seismic Station(epicenter distance 85 km) |
|
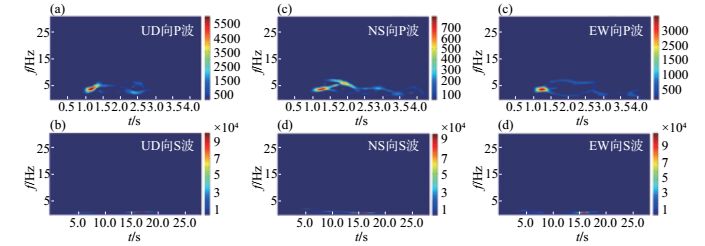
图 6 阿拉善左旗ML 3.0爆破石嘴山台记录的波形时频结果(震中距50 km) Fig.6 Time-frequency results of seismic waveforms of ML 3.0 Alxa Left Banner blasting recorded at Shizuishan Seismic Station (epicenter distance 50 km) |
| 表 1 数字地震波时频结果主要参数 Tab.1 Time-frequency results' main parameters of digital seismic waveforms |
(1) 乌海台记录的阿拉善左旗ML 3.8地震。由图 3、表 1可见:① UD、NS、EW向P波高能量密度区域(谱峰值集中区域)频宽分别为25 Hz、16 Hz、19 Hz,S波高能量密度区域频宽分别为13 Hz、14 Hz、16 Hz;②P波能量密度比S波能量密度小1个数量级;③EW向S波时频分布图能清晰地显示出地震波衰减特征,高能量密度位于高频段时间延续短,位于低频段时间延续长。
(2) 石嘴山台记录的阿拉善左旗ML 3.8地震。由图 4、表 1可见:①记录的UD、NS、EW方向P波高能量密度区域频宽分别为19 Hz、18 Hz、26 Hz,S波高能量密度区域频宽分别为13 Hz、14 Hz、16 Hz;②P波能量密度比S波能量密度小1个数量级。
2.2 阿拉善左旗ML3.0爆破(1) 乌海台记录的阿拉善左旗ML 3.0爆破。由图 5、表 1可见:①UD、NS、EW方向P波高能量密度区域频宽分别为11 Hz、6 Hz、6 Hz,S波高能量密度区域频宽分别为11 Hz、8 Hz、8 Hz;②P波能量密度比S波能量密度小1个数量级。
(2) 石嘴山台记录的阿拉善左旗ML 3.0爆破。由图 6、表 1可见:① UD、NS、EW方向P波高能量密度区域频宽分别为12 Hz、7 Hz、7 Hz,S波高能量密度区域频宽分别为5 Hz、5 Hz、4 Hz;② P波能量密度比S波能量密度小1个数量级。
2.3 结果分析通过对天然地震及爆破事件进行ZAM时频分析,结果表明:①包括天然地震和爆破在内的数字地震波形中,S波高能量密度区域处于低频段,其频带比P波高能量密度区域频带窄,且其能量密度比P波能量密度大1个数量级;②天然地震的高能量密度分布较为离散,爆破的高能量密度分布区域集中。
3 讨论和结论ZAM方法为非线性时频分析方法,其核函数为锥形核函数,研究表明,拥有此类核函数的时频方法适合对数字地震波等非平稳信号进行分析。ZAM时频分析方法能有效抑制时频结果中的交叉干扰项,同时使时频结果具有较高聚集性,在数字地震研究中具有广泛的应用前景(张帆等,2006;张晔,2006;姚家骏等,2011)。
时频分析具有时间分辨率与频率分辨率相矛盾、高聚集性和低交叉项相矛盾等特点,选取赵—阿特拉斯—马克斯(ZAM)方法,进行数字地震波时频处理,得到以下结论:S波高能量密度区域处于低频段,其频带比P波高能量密度区域频带窄,且其能量密度比P波能量密度大1个数量级;天然地震的高能量密度分布较为离散,爆破的高能量密度分布较集中。
通过时频分析可清晰、直观地显示数字地震波所包含信息的优势频段和时段,能形象展示频谱特征随时间的变化,弥补了时序曲线仅显示信息的时域特征或频谱曲线仅显示频域特征等缺憾,为充分挖掘有效信息提供了可能,在今后将有广阔的应用前景。
在本研究过程中,中国地震台网中心提供地震目录,内蒙古自治区地震监测中心测震台网提供数字地震波形资料,在此一并表示感谢。
| 陈友良. 时频分析在地震信号处理中的研究及应用[D]. 长沙: 中南大学, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1916259 | |
| 陈学华, 贺振华. 改进的S变换及在地震信号处理中的应用[J]. 数据采集与处理, 2005, 20(4): 449-453. | |
| 陈斌. 时频分析及在地震信号分析中的应用研究[D]. 成都理工大学, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1068448 | |
| 葛哲学, 陈仲生. MATLAB时频分析技术及其应用[M]. 北京: 人民邮电出版社, 2006. | |
| 高军, 凌云, 周兴元, 等. 时频域球面发散和吸收补偿[J]. 石油地球物理勘探, 1996, 31(6): 856-866. | |
| 刘希强, 周蕙兰, 李红. 基于小波包变换的地震数据时频分析方法[J]. 西北地震学报, 2000, 22(2): 143-146. | |
| 刘希强, 沈萍, 李红, 等. 高斯线调频连续小波变换的时频能量衰减因子方法及其应用[J]. 中国地震, 2003, 19(3): 225-235. | |
| 刘希强, 沈萍, 山长仑, 等. 数字化地震波形资料的时频分析方法及应用[J]. 西北地震学报, 2004, 26(2): 118-125. | |
| 刘丽娟. 时频分析技术及其应用[D]. 成都理工大学, 2008. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=jxkx200901018&dbname=CJFD&dbcode=CJFQ | |
| 王培茂. 地震信号的时频特征表示方法及应用[D]. 长春: 吉林大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10183-2008126927.htm | |
| 万永革. 数字信号处理的MATLAB实现[M]. 北京: 科学出版社, 2012. | |
| 许朝阳, 季国华, 刘俊民, 等. 时频分析技术在地震信号初至估计中的应用[J]. 核电子学与探测技术, 2008, 28(5): 987-990. | |
| 许康生. 地震信号的时-频分析[J]. 西北地震学报, 2000, 22(4): 479-482. | |
| 姚家骏, 杨立明, 冯建刚. 常用时频分析方法在数字地震波特征量分析中的应用[J]. 西北地震学报, 2011, 33(2): 105-110. | |
| 杨彦明, 张文韬, 张帆, 等. 内蒙古地震监测台网的建设与发展[J]. 高原地震, 2013, 25(2): 22-25. | |
| 杨彦明, 戴勇, 张国清, 等. 内蒙古中西部地区地震烈度衰减关系[J]. 地震地磁观测与研究, 2016, 37(1): 30-37. | |
| 张帆, 钟羽云, 朱新运, 等. 时频分析方法及在地震波谱研究中的应用[J]. 地震地磁观测与研究, 2006, 27(4): 17-22. | |
| 张帆. 地震波时频谱分析及其在爆破识别中的应用[D]. 合肥: 中国科学技术大学, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D344696 | |
| 张晔. 信号时频分析及应[M]. 哈尔滨工业大学出版社, 2006. | |
| Cohen L. Time-frequency distributions-a review[J]. Proceedings of the IEEE, 1989, 77(7): 941-981. DOI:10.1109/5.30749 | |
| Cohen L. Time-frequency analysis: Theory and application[M]. Englewood Cliffs: Prentice Hall, 1995, 25-27. | |
| Chant I J, Hastie L M. Time-frequency analysis of magneto-telluric data[J]. Geophysical Journal Inter-national, 1992, 111(2): 399-413. DOI:10.1111/gji.1992.111.issue-2 | |
| Gabor D. Theory of communication.Part 1:The analysis of information[J]. Journal of the Institution of Electrical Engineers-Part Ⅲ: Radio and Communication Engineering, 1946, 93(26): 429-441. DOI:10.1049/ji-3-2.1946.0074 | |
| Jones D L, Baraniuk R G. An adaptive optimal-kernel time-frequency representation[J]. IEEE Trans actions on Signal Processing, 1995, 43(10): 2 361-2 371. DOI:10.1109/78.469854 | |
| Potter R K, Kopp G A, Green H C. Visible speech[M]. New York: Van Nostran, 1947. | |
| Utsu T. On the nature of three Alaskan aftershock sequences of 1957 and 1958[J]. Bulletin of the Seismological Society of America, 1962, 52(2): 279-297. | |
| Ville J. Theorie et applications de la notion de signal analytique[J]. Cables et Transmission, 1948, 2A: 61-74. |
 2017, Vol. 38
2017, Vol. 38

