地震数据一般直接存储为SEED格式。SEED格式是国际通用的数字地震数据交换格式，具有数据布局方式科学合理、管理和存储方便、环境适应广等特点。SEED文件由2部分组成：①头文件，包含记录开始时刻、数据记录时长、采样频率、通道名、台站经纬度、台站名、台站设备参数等参数；②数字地震观测系统记录的观测数据。

上海市数字地震遥测台网由34个测震地震台站组成，其中国家基准地震台1个(佘山地震台)、区域遥测台13个。上海地震台站布点较密，上海市地震台网中心日产出数据文件15 G—16 G。数据量过大时会造成数据存储效率的降低，如对SEED格式文件直接压缩，由于未优化该格式文件的数据结构，压缩效率不高。

近年来，国内外地震工作者和物探勘察工程师利用小波变换方法，对地震数据压缩进行研究，主要集中于地震波形数据的二维图像压缩领域(唐向宏，1999；杨浩钦，2007)和地球物理勘探领域(唐向宏，1999；武文波，2005)，而对“十五”数字化改造后地震观测台产出的数字地震波形数据进行小波分析的研究尚未进行。本文以上海市地震监测中心实际工作为基础，尝试采用Mallat算法，对数字地震信号记录文件进行数据优化和重构，分别选取bior系列函数、db系列函数、sym系列函数共计9个不同的小波分解函数，对不同类型的数字地震波形进行3—5层的小波分解，并对得到的小波细节进行分层硬阈值优化运算，对重构信号进行数据压缩，并对压缩结果进行分析。

1989年，Mallat提出信号的塔式多尺度分析与重构的快速算法，即马拉特(Mallat)算法。使用Mallat算法对信号进行正交小波变换与信号镜像滤波效果相同，输出高频分量和低频分量，分别称之为细节分量D和近似分量A。以最高频率为10 Hz的信号为例，经过镜像滤波后被分解为频段为0—5 Hz的信号(低通滤波器信号)和频段为5—10 Hz的信号(高通滤波器信号)，将低频信号继续进行镜像滤波分解，原始信号即被分解为频段0—2.5 Hz(第2层低通滤波)、2.5—5 Hz(第2层高通滤波)和5—10 Hz(第1层高通滤波)的信号。如图 1所示，采用循环滤波过程即采用Mallalt算法，可以将原始信号分解为一系列不同频率的信号。

图 1(Fig. 1)

图 1 Mallat算法示意 Fig.1 Schematic diagram of Mallat algorithm

本文选取地震观测台站噪声数据、地震观测系统正弦标定数据、地震观测系统脉冲标定数据，短周期地震计地震事件数据和宽频带地震计地震事件数据等5段具有代表性的地震记录波形进行研究。原始记录波形均为SEED格式，为便于研究及计算，对选取的数字地震波形数据文件进行预处理，即将SEED文件按通道导出为ASCII格式文件。为研究方便，只选取垂直向信号做信号分析和数据压缩。选取的5个数字地震波形文件经预处理后主要参数见表 1。

表 1(Tab. 1

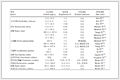
表 1 待分析数字地震波形文件主要参数Tab. 1 The main parameters of digital seismic waveform file to be analyzed 序号 数据类型 原始文件/kb 直接压缩文件/kb 数据时长/s 采样点数 1 宽频带地震事件 183 44 104 10 400 2 短周期地震事件 79.18 32.25 120 12 000 3 噪声文件 3298 438.25 940 188 000 4 正弦标定文件 613.47 123.27 349 34 900 5 脉冲标定文件 214.45 31.56 122 12 200

表 1 待分析数字地震波形文件主要参数 Tab.1 The main parameters of digital seismic waveform file to be analyzed

本文使用的数据分析方法主要采取数据载入、小波分解、阈值运算、重构比较、数据压缩和结果分析等步骤，具体操作步骤为：①将预处理后只包含纯数据的数字地震波形文件载入Matlab运算内存；②进行小波变换，小波分解的输出结构包括小波分解向量c和相应记录向量l(周智勇，2001)；③通过Birge—Massart算法，得到不同层数的阈值结果，采用硬阈值计算方法，每层系数中小于该层阈值的系数置零，得到新的小波分解向量c′，结合记录向量l，重构数字地震信号波形；④通过作图比较重构信号与原始信号，查看是否存在畸变等现象，并对二者进行数值比较，计算误差的平均值和最大值等参数；⑤将新的小波分解向量c′和结构向量输出l的输出结果进行数据压缩；⑥将数字地震波形文件直接压缩得到的文件与利用Mallat算法进行压缩得到的文件进行大小比较。

对噪声文件、正弦标定记录、脉冲标定记录、宽频带地震事件记录、短周期地震事件记录等5个不同类型的数字地震记录进行不同分解参数的小波变换，文中选择bior2.4、bior2.6、bior2.8、db3、db4、db5、sym3、sym4、sym5共9种小波为小波分解基函数，分解层数为3—5，即对每个波形文件进行27次小波分解。通过重构信号与原始信号采样点数据误差的比较，分析得出，随着分解层数的增加，相同小波分解函数下重构信号能够得到更高压缩比，但是与原始信号之间的误差，能量保留系数逐渐降低，因此分解层数不易过大，以4层为佳。表 2—表 6分别给出不同类型地震记录在不同分解参数下的分析结果。

表 2(Tab. 2

表 2 噪声文件不同参数小波分解结果Tab. 2 Different parameters of wavelet decomposition results (noise file) 序号 小波函数 分解层数 误差最大值 误差平均值 能量保留(%) 压缩文件/kb 1 bior2.4 3 171.117 9 31.326 2 99.65 280 2 4 299.380 1 53.671 9 98.88 180 3 5 491.392 3 80.058 2 97.40 123 4 bior2.6 3 173.965 7 31.333 2 99.64 280 5 4 312.567 9 53.814 1 98.83 180 6 5 561.110 2 80.236 9 97.32 123 7 bior2.8 3 172.673 2 31.459 3 99.63 280 8 4 314.405 54.066 3 98.81 180 9 5 570.248 9 80.445 6 97.27 123 10 db3 3 192.238 7 32.407 1 99.63 281 11 4 303.838 8 54.476 2 98.96 179 12 5 516.698 7 80.638 7 97.69 122 13 db4 3 177.800 6 31.365 8 99.65 280 14 4 309.483 3 53.514 3 98.99 179 15 5 510.971 5 79.366 6 97.76 122 16 db5 3 182.567 4 31.027 7 99.66 281 17 4 314.292 3 52.815 8 99.02 179 18 5 460.369 9 78.330 3 97.82 122 19 sym3 3 192.238 7 32.407 1 99.63 281 20 4 303.838 8 54.476 2 98.96 179 21 5 516.698 7 80.638 7 97.69 122 22 sym4 3 178.083 4 31.472 3 99.65 281 23 4 311.007 4 53.484 5 98.99 179 24 5 587.222 79.275 4 97.77 122 25 sym5 3 162.825 7 30.920 1 99.66 281 26 4 307.972 5 52.643 1 99.02 179 27 5 539.029 78.198 6 97.83 122

表 2 噪声文件不同参数小波分解结果 Tab.2 Different parameters of wavelet decomposition results (noise file)

表 3(Tab. 3

表 3 正弦标定文件不同参数小波分解结果Tab. 3 Different parameters of wavelet decomposition results (sine calibration data) 序号 小波函数 分解层数 误差最大值 误差平均值 能量保留(%) 压缩文件/kb 1 bior2.4 3 7 812.700 0 550.466 1 99.999 9 49 2 4 33 031.000 0 1927.800 0 99.998 8 32 3 5 119 790.000 0 8051.800 0 99.984 4 22 4 bior2.6 3 8 520.000 0 549.533 7 99.999 9 50 5 4 31 055.000 0 1929.700 0 99.998 8 32 6 5 118 560.000 8075.300 0 99.984 6 22 7 bior2.8 3 8 151.100 0 548.670 0 99.999 9 50 8 4 34 819.000 0 1935.400 0 99.998 8 32 9 5 114 040.000 0 8060.400 0 99.984 9 22 10 db3 3 1 383.400 0 107.683 3 100.000 0 52 11 4 10 935.000 0 619.821 6 99.999 9 33 12 5 80 416.000 0 4777.700 0 99.995 9 23 13 db4 3 226.696 0 44.065 1 100.000 0 54 14 4 1 828.900 0 133.965 7 100.000 0 35 15 5 26 773.000 0 1479.300 0 99.999 6 24 16 db5 3 201.961 2 40.078 3 100.000 0 55 17 4 357.296 0 64.117 2 100.000 0 35 18 5 8 562.300 0 530.262 0 100.000 0 24 19 sym3 3 1 383.400 0 107.683 2 100.000 0 52 20 4 10 935.000 0 619.821 6 99.999 9 33 21 5 80 416.000 0 4777.7000 99.995 9 23 22 sym4 3 233.131 5 44.203 7 100.000 0 54 23 4 1 761.100 0 132.050 0 100.000 0 35 24 5 27 099.000 0 1457.700 0 99.999 6 24 25 sym5 3 238.806 5 40.058 3 100.000 0 55 26 4 388.620 1 63.633 7 100.000 0 35 27 5 7 764.800 0 504.875 6 100.000 0 24

表 3 正弦标定文件不同参数小波分解结果 Tab.3 Different parameters of wavelet decomposition results (sine calibration data)

表 4(Tab. 4

表 4 脉冲标定文件不同参数小波分解结果Tab. 4 Different parameters of wavelet decomposition results (pulse calibration data) 序号 小波函数 分解层数 误差最大值 误差平均值 能量保留(%) 压缩文件/kb 1 bior2.4 3 74.186 4 16.886 3 100.000 0 20 2 4 134.191 4 22.109 9 100.000 0 13 3 5 650.746 1 31.630 8 100.000 0 9 4 bior2.6 3 80.599 1 16.996 5 100.000 0 20 5 4 147.892 22.236 9 100.000 0 13 6 5 588.723 6 32.039 100.000 0 9 7 bior2.8 3 76.177 3 16.978 6 100.000 0 20 8 4 130.837 6 22.479 8 100.000 0 13 9 5 892.751 4 32.241 7 100.000 0 9 10 db3 3 80.640 3 16.137 3 100.000 0 21 11 4 103.532 1 21.018 8 100.000 0 13 12 5 149.288 1 28.268 5 100.000 0 9 13 db4 3 72.494 5 16.100 9 100.000 0 21 14 4 104.813 7 20.943 9 100.000 0 13 15 5 126.813 7 27.821 4 100.000 0 9 16 db5 3 72.028 6 15.826 5 100.000 0 21 17 4 98.326 5 20.431 8 100.000 0 14 18 5 135.981 1 27.013 100.000 0 9 19 sym3 3 80.640 3 16.137 3 100.000 0 21 20 4 103.532 1 21.018 8 100.000 0 13 21 5 149.288 1 28.268 5 100.000 0 9 22 sym4 3 70.274 15.970 5 100.000 0 21 23 4 99.938 7 20.544 3 100.000 0 13 24 5 131.840 4 27.168 1 100.000 0 9 25 sym5 3 70.597 3 15.997 4 100.000 0 21 26 4 90.298 6 20.340 2 100.000 0 14 27 5 128.842 6 26.796 2 100.000 0 9

表 4 脉冲标定文件不同参数小波分解结果 Tab.4 Different parameters of wavelet decomposition results (pulse calibration data)

表 5(Tab. 5

表 5 短周期地震事件不同参数小波分解结果Tab. 5 Different parameters of wavelet decomposition results (short-period seismometer earthquake event data) 序号 小波函数 分解层数 误差最大值 误差平均值 能量保留(%) 压缩文件/kb 1 bior2.4 3 5 606.600 0 775.159 1 99.970 4 20 2 4 15 776.000 2 051.600 0 99.779 7 13 3 5 40 349.000 0 4 775.300 0 98.978 2 9 4 bior2.6 3 6 390.400 0 799.650 3 99.968 5 20 5 4 16 649.000 2 081.500 0 99.774 8 13 6 5 39 796.000 0 4 817.700 0 98.981 8 9 7 bior2.8 3 5 830.200 0 795.899 4 99.967 6 20 8 4 15 903.000 0 2 088.600 0 99.767 6 13 9 5 37 763.000 0 4 701.700 0 99.019 6 9 10 db3 3 7 387.000 0 808.836 3 99.968 1 20 11 4 19 201.000 0 2 231.600 0 99.738 8 13 12 5 38 968.000 0 5 204.900 0 98.600 2 9 13 db4 3 5 254.800 0 747.503 6 99.972 7 20 14 4 16 441.000 0 1 969.300 0 99.798 7 13 15 5 39 514.000 0 4 531.500 0 98.899 6 9 16 db5 3 5 760.600 0 711.866 7 99.974 9 20 17 4 16 999.000 0 1 992.200 0 99.784 0 13 18 5 35 091.000 0 4 487.400 0 98.950 6 9 19 sym3 3 7 387.000 0 808.836 3 99.968 1 20 20 4 19 201.000 0 2 231.600 0 99.738 8 13 21 5 38 968.000 0 5 204.900 0 98.600 2 9 22 sym4 3 5 801.500 0 733.919 2 99.973 0 20 23 4 17 645.000 0 2 069.900 0 99.771 3 13 24 5 36 517.000 0 4 837.000 0 98.814 5 9 25 sym5 3 4 836.500 0 691.550 5 99.976 1 20 26 4 17 543.000 0 1 902.100 0 99.808 1 13 27 5 38 035.000 0 4 376.600 0 98.986 4 9

表 5 短周期地震事件不同参数小波分解结果 Tab.5 Different parameters of wavelet decomposition results (short-period seismometer earthquake event data)

表 6(Tab. 6

表 6 宽频带地震事件不同参数小波分解结果Tab. 6 Different parameters of wavelet decomposition results (broadband seismometer earthquake event data) 序号 小波函数 分解层数 误差最大值 误差平均值 能量保留(%) 压缩文件/kb 1 bior2.4 3 46 849.0 6 048.0 99.995 9 17 2 4 136 850.0 17 120.0 99.964 5 11 3 5 396 300.0 45 020.0 99.746 3 8 4 bior2.6 3 41 773.0 5 766.9 99.996 3 17 5 4 131 900.0 17 839.0 99.960 2 11 6 5 328 930.0 44 027.0 99.752 3 8 7 bior2.8 3 47 257.0 6 114.8 99.995 7 17 8 4 153 860.0 17 605.0 99.961 5 11 9 5 385 860.0 43 528.0 99.755 8 8 10 db3 3 42 678.0 6 255.7 99.995 7 17 11 4 164 370.0 18 720.0 99.958 8 11 12 5 449 320.0 48 316.0 99.703 5 8 13 db4 3 37 596.0 5 391.8 99.996 8 17 14 4 125 690.0 17 119.0 99.965 5 11 15 5 368 500.0 44 964.0 99.751 1 8 16 db5 3 38 970.0 5 073.6 99.997 2 17 17 4 112 030.0 15 557.0 99.972 8 11 18 5 374 000.0 43 609.0 99.772 1 8 19 sym3 3 42 678.0 6 255.7 99.995 7 17 20 4 164 370.0 18 720.0 99.958 8 11 21 5 449 320.0 48 316.0 99.703 5 8 22 sym4 3 35 864.0 5 362.2 99.996 9 17 23 4 128 660.0 16 630. 99.968 7 11 24 5 389 730.0 44 038.0 99.760 3 8 25 sym5 3 35 512.0 4 912.3 99.997 4 17 26 4 111 400.0 15 966.0 99.971 7 11 27 5 344 940.0 41 632.0 99.794 5 8

表 6 宽频带地震事件不同参数小波分解结果 Tab.6 Different parameters of wavelet decomposition results (broadband seismometer earthquake event data)

对比表 2—表 6的分析结果可知，选取4层小波分解层数，随着小波分解函数长度的增加，使用bior函数系列计算时，重构噪声信号与原始信号之间误差变大，但变化幅度不大；重构正弦标定信号、重构脉冲标定信号、重构短周期地震事件信号与原始信号之间，均存在误差最大值无明显变化，但平均值变大现象；重构宽频带地震事件信号与原始信号之间误差水平无明显变化。使用dbN函数系列计算时，重构噪声信号、重构脉冲标定信号与原始信号之间，均存在误差最大值变大而平均值变小的现象；重构正弦标定信号与原始信号误差水平变小；重构短周期地震事件信号与原始信号之间误差水平无明显变化；重构宽频带地震事件信号与原始信号之间误差水平变小。使用sym函数系列计算时，重构噪声信号与原始信号之间误差最大值无明显变化，但平均值变小；重构正弦标定信号、重构脉冲标定信号、重构短周期地震事件信号、宽频带地震事件信号与原始信号之间，均存在误差水平变小的现象。

综合比较上述5种具有代表性的数字地震波形数据文件小波分解及数据压缩结果，可以得出以下结论。

(1) 小波变换算法用于数字地震信号压缩具有可操作性。对原始信号进行小波分解并进行阈值运算后，可对小波系数进行zip压缩。由于处理后小波系数中零系数比例提高，小波系数的压缩文件相比于原始信号的直接压缩文件，文件存储效率提高2—4倍。

(2) 采用不同小波函数，但采用相同的分解层数，对同一个数字地震波形数据文件进行分解、压缩的效果基本相同，即文件压缩效率与所选取的小波函数无关，而只与小波分解层数有关。因重构信号与原始信号间误差随着分解层数的增加而变大，而能量保留比例随之变小，进行4层小波分解为宜。

(3) 对地震噪声数据文件、地震观测系统正弦标定文件、脉冲标定文件、短周期地震计地震事件文件而言，选取sym5函数作为小波分析的基函数，重构信号与原始信号的误差平均值最小，对于宽频带地震计地震事件的文件而言，选取db5函数作为分解基函数得到的重构信号误差平均值最小，使用sym5函数效果次之，但二者相差不大。

(4) 使用sym5小波对数字地震数据文件完成4层分解，以阈值运算后的小波分解向量重构得到的新地震信号与原始信号相比较，地震波形恢复情况好，重构信号满足地震定位、地震观测系统参数测算、台站噪声谱分析等地震日常工作和科研工作的需求。