0 引言

地球内部的“不可入性”及大震的“非频发性”给地震预测研究带来诸多困难（陈运泰，2007）。地震的发生往往伴随着地下介质结构及特性的变化，而介质的变化又会导致地震波速的变化（王伟涛等，2009）。地震波携带了大量的地下介质信息（杨微等，2015），通过对接收到的地震波进行研究，可以了解地下介质结构组成及特性的变化，对地震预测具有重要意义。

天然地震由于受时空分布的限制(王宝善等，2016)，难以利用天然地震波对地下介质进行系统研究及动态监测。人工震源具有重复性好、频率可控等优点，已成为波速精确测量的一个重要手段（杨微等，2016），并广泛应用于地壳结构探测、地下介质变化监测及石油、天然气开采等领域（杨微等，2013）。

当震源距较远时，由于地层对地震波的作用及周边环境的干扰，难以直接利用台站记录数据准确提取震相。反卷积是人工震源数据处理中的一个重要方法。传播路径的格林函数携带了地下介质相关信息（翟秋实等，2016），通过反卷积计算，可以去除记录信号中的震源子波，得到的波形不受震源扫描信号特征的影响，且能够保留传播路径格林函数的相位信息（杨微等，2013），从而使通过反卷积计算地震波走时成为可能。本文首先对利用反卷积去除震源子波过程进行推导，并以河北赤城—张北精密可控震源实验为例，研究反卷积在人工震源数据处理中的相关问题。

1 理论

地表震源激发的信号，会向地下各个方向发射，每一个方向的波称之为震源子波。当震源子波在传播过程中遇到地下波阻抗界面时，会反射回地表，被台站传感器接收，不同方向的子波会经过不同的路径到达地表同一地点，且每一子波在传播反射过程中都伴随着时间的延迟及能量的变化。地震台站记录到的地震信号可用公式（1）表示（刘喜武等，2003）。

$ y\left(t \right) = \sum {_{i = 1}^\infty {r_i}s\left({t - {\tau _i}} \right) + n\left(t \right)} $

(1)

其中，y(t)为接收台站记录信号，s(t)为震源子波，r_i为子波经第i条路径传播到接收台站的地层响应系数（表征该子波能量的变化），τ_i为子波经第i条路径传播到接收台站的时间，n(t)为噪声。

因此，记录信号可看作是不同震源子波信号经过时移加权叠加的结果。定义一个地层响应函数r(t)，令r(τ_i) = r_i，代入式（1），得到$y\left(t \right) = \sum {_{i = 1}^\infty {r_i}s\left({t - {\tau _i}} \right) + n\left(t \right)} = $$ \sum {_{i = 1}^\infty r\left({{\tau _i}} \right)s\left({t - {\tau _i}} \right) + n\left(t \right) = r\left(t \right)*s\left(t \right) + n\left(t \right)} $，即

$ y\left(t \right) = r\left(t \right)*s\left(t \right) + n\left(t \right) $

(2)

引入噪声n(t)，主要是考虑到观测场地噪声对记录数据的影响。由于接收台站选址通常远离人类活动密集区，且震源信号设定在特殊频段，在实际处理数据时可忽略n (t)项。

根据卷积定理，即F [r(t)*s(t) ] = F [r(t)] F [s(t) ] = R(w) S(w)，对公式（2）两侧进行傅氏变换，忽略n(t)项，可得Y(w) = R(w) S(w)，R(w) = Y(w) / S(w)，再对两侧进行傅氏逆变换，可求得地层响应函数r(t)（杨微等，2013），即

$ r\left(t \right) = {F^{ - 1}}\left[ {Y\left(w \right)/S\left(w \right)} \right] $

(3)

上述即为利用反卷积去除震源子波，求解地层响应函数r(t)的过程。

进一步对r(t)进行分析，$ r\left(t \right)*\delta \left(t \right) = \sum {_{i = 1}^\infty r\left({{\tau _i}} \right)\delta \left({t - {\tau _i}} \right)} $，其中δ(t)为单位冲激函数。由$ \delta \left({t - {\tau _i}} \right) = \left\{ \begin{array}{l} 1\left({{\tau _i} = t} \right)\\ 0\left({{\tau _i} \ne t} \right) \end{array} \right.$，可得$ \sum {_{i = 1}^\infty r\left({{\tau _i}} \right)\delta \left({t - {\tau _i}} \right)} = r\left(t \right)$。又r(τ_i) = r_i，所以$\sum {_{i = 1}^\infty r\left({{\tau _i}} \right)\delta \left({t - {\tau _i}} \right)} = \sum {_{i = 1}^\infty {r_i}\delta \left({t - {\tau _i}} \right)} $，即

$ r\left(t \right) = \sum {_{i = 1}^\infty {r_i}\delta \left({t - {\tau _i}} \right)} $

(4)

因此，地层响应函数可分解为众多时移加权的单位冲激信号的和。τ₁为初至波传播时间，即P波走时。当t < τ₁时，震源信号未传播到接收台站，r(t) = 0，因此，r(t)函数波形中第一个突跳值即为r₁，对应的时间即为τ₁。

2 实验

采用北京港震机电技术有限公司生产的CASS-40精密可控主动震源系统，通过精密控制2个质量体的旋转频率以确保输出弹性波的频率；精密控制2个质量体的旋转相位以确保输出弹性波的相位；用GPS给精密可控主动震源和数据接收系统授时和定位，以保证弹性波发出及接收到的时间精度和位置精度。该震源系统具有大吨位（10 Hz时最大输出力可达40 t）、高稳定性、扫描信号可人工设计、信号传播距离远等优点。

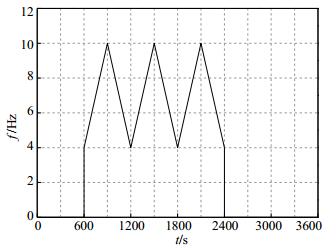
实验选用线性调频模式，设计扫描频率为4—10 Hz，每小时运行3个周期，变频扫描模式见图 1。在整个实验过程中，震源24小时不间断运行。

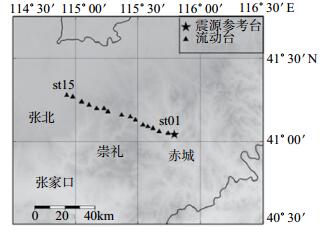
CASS-40精密可控主动震源系统架设在河北省赤城县，在震源处架设一套观测系统，作为参考台站（编号:ckt）；并沿赤城—张北地区布设15个流动台站（编号:st01—st15），台站间距约5 km，形成一条测线，用以接收震源信号，测线分布见图 2。

参考台站选用北京港震机电技术有限公司生产的FSS-3M型地震计，频带宽度为2 s—80 Hz，动态范围大于120 dB，不易限幅；流动台站选用GURALP公司生产的CMG-40TDE便携式一体化地震仪，频带宽度为1 s—100 Hz。

3 数据分析

计算过程选取参考台站及流动台站的垂直分向记录，数据存储及计算单元均为1小时。

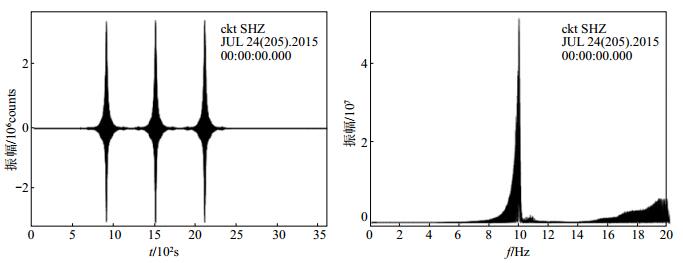
3.1 震源信号特征

参考台（ckt）记录的震源信号波形见图 3(a)，对其进行快速傅氏变换（Fast Fourier Transformation，FFT），得到振幅谱，见图 3(b)。可以看到，在扫描频段4—10 Hz范围内，振幅随频率呈2次方规律增大，在10 Hz时达到峰值，震源输出力最大。

3.2 震源重复性

利用地震波研究地下介质变化，要求震源具有较好的重复性，才能保证监测到的波速变化是由地下介质变化导致的，而不是由于震源不稳定造成的。震源稳定性需从能量的稳定和激发时刻的稳定进行研究。

用参考台站（ckt）数据表征震源信号，选取1小时数据作为参考，对其他数据沿时间轴进行扫描，应用公式（5）计算扫描过程中的相关系数，并记录相关系数最大时刻。

$ r\left(d \right) = \frac{{\sum {_i\left[ {\left({x\left(i \right) - mx} \right)\left({y\left({i - d} \right) - my} \right)} \right]} }}{{\sqrt {\sum {_i{{\left[ {(x\left(i \right) - mx} \right]}^2}} } \sqrt {\sum {_i{{\left[ {(y\left({i - d} \right) - mx} \right]}^2}} } }} $

(5)

其中，r (d)为相关系数，d为扫描偏移量，x (i)为参考信号记录值，y (i)为被扫描信号值，mx和my为均值。

经计算，2015年7月24日—8月6日震源运行期间，所有数据相关系数均在0.99以上，且激发时刻误差均在0.02 s以内，该震源系统具有较高重复性。

3.3 地层响应函数提取

对所有数据进行4—10 Hz带通滤波处理，并应用公式（3）进行反卷积计算，求出震源与接收台站之间的地层响应函数r(t)。为提高信噪比，把同一台站所有小时单元地层响应函数r(t)进行叠加，暂不考虑r(t)随地下介质的动态变化，图 4给出地层响应函数剖面图。可以看出，通过反卷积方法，能够得到各传播路径地层响应函数，并能够较精确提取地震波走时。通过计算，赤城—张北地区P波波速约6 km/s。

当震源距在75 km以上时，信号分辨率较低，这是因为:①本实验震源采用线性调频模式，虽易于操作和实现，但决定传播距离的低频成分能量明显偏低（崔仁胜等，2017），而随着传播距离增大，高频成分又容易衰减和散射（林建民等，2008）；②st15观测台基为土层型，接收信号能力较弱。

4 结论

通过上述理论推导及实验研究，可以得到以下结论:①记录信号是众多震源子波经过时移加权叠加的结果；②利用反卷积可以去除震源子波信息，提取研究区域地层响应函数；③地层响应函数可分解为众多时移加权的单位冲激信号的和，函数波形中第一个突跳值对应的时间即为地震P波走时；④通过计算，河北赤城—张北地区P波波速约6 km/s。

基于人工震源实验，可以通过波速变化对地下介质变化进行长期动态监控。不同区域尺度介质结构及应力差异，以及不同时间尺度的介质变化有待进一步研究。