1950 — 2007年,中国地震监测积累了大量模拟记录图纸。然而,很多珍贵地震图纸面临腐烂、损坏的危险,有些地震监测手段已完成数字化改造,但个别手段仍采用模拟记录方式进行地震监测。在地震模拟监测记录资料的保存与使用上,有单位将模拟记录图纸进行扫描存档,但读取、使用不便,因此提出将模拟记录资料进行数字化的研究与试验,以完成模拟记录成果数字化。将地震模拟记录纸带的历史资料以数字化存储,易于管理、备份、应用及共享服务,重要的是,现今保存完好的模拟记录图纸,即使将来腐烂或损毁,也不影响数字化资料的使用,可对地震分析、预测等研究提供坚实的数据支撑,因为历史震例的回溯性研究是地震分析、预测的学习过程,也是对历史震例重新认识、不断升华的过程(石富强,2015)。
图像矢量化是数字图像处理中的一个重要问题,是一个综合了计算机视觉、计算机图像处理、计算机图形学和人工智能等多个学科的交叉课题。矢量图像有很多优点:首先,矢量图像由简单的几何图元组成,表示紧凑,所占存储空间小;其次,矢量图像易于进行编辑,对矢量图像进行编辑的时候, 如进行旋转、拉伸、平移等操作时仅需要修改相应几何图元的参数信息;第三,用矢量表示的对象易于放大或者压缩,而且不会降低其在计算机中的显示质量,矢量图像的放缩能够保持边角的尖锐等特性,不会出现模糊现象,影响显示质量(朱婧,2001)。基于以上矢量图像的优点,本文从数字化模块设计到功能实现,以实例展现地震监测模拟记录图纸的数字化,并与人工读取结果进行对比,展示其优越性。
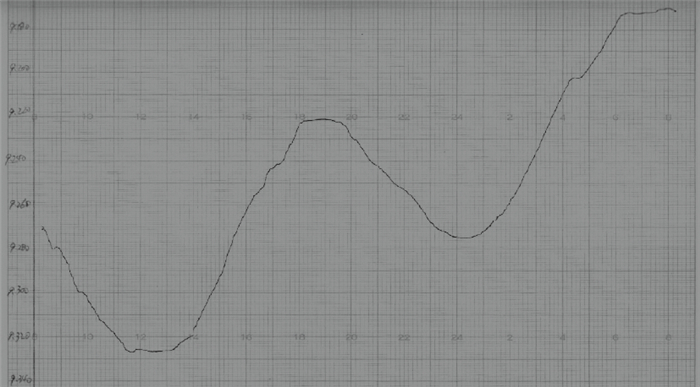
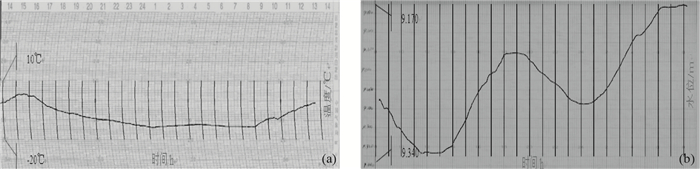
1 研究现状栅格图形矢量化在测绘行业比较成熟,但其转换方法对于地震行业模拟记录图纸的数据矢量化不太适用,因为:①测绘图形是由点、线、面构成的,图形之间无交叉、压盖,且为高斯直角坐标系,而地震行业的监测手段多,对应的图纸种类也较多,图纸多具有网格背景,存在网格与记录曲线的重叠;②虽然存在直角坐标格网的模拟记录纸带(图 1为水位观测记录纸带,横坐标为小时,纵坐标为以m为单位的水位),但有些模拟记录纸带使用的轴系中的坐标纵轴线(横坐标通常表现为时间序列)并非直线(图 2为每日温度记录纸带,横坐标为小时,纵坐标为以℃为单位的温度),而进行数字化处理的计算机屏幕坐标系是直角坐标,因此,地震模拟监测资料的时间线数据和记录曲线的获取,是图像矢量化存在的难题。
|
图 1 水位观测记录纸带 Fig.1 Water level record |

|
图 2 每日温度记录纸带 Fig.2 Temperature record per day |
特征线作为线状地物专题信息的一种,矢量化时需依次记录每个格网的坐标,即对栅格特征数据进行追踪(孔月萍,2013)。同样地,地震模拟记录图纸上的曲线是矢量化的特征线,而图纸具有坐标网格背景(如图 1、图 2中的纵横坐标线),因此曲线矢量化前应配置坐标网格,进行模拟记录曲线的提取,此时获得图像坐标系下的图表,称之为影像图表;将影像图表通过转换关系转换到实际图表,批量获取或点取所需时刻的测量记录值。模拟图纸数字化流程见图 3。

|
图 3 数字化流程 Fig.3 Flow chart of digitization |
基于Matlab,实现地震模拟记录图纸数字化功能。数字化过程中所获取的图表包括影像图表和实际图表(图 3)。其中,影像图表部分包括:影像旋转、拟提取色彩取样设置、坐标轴线匹配、坐标定义及曲线提取。实际图表部分包括:轴线与曲线交点坐标提取、交点坐标到实际坐标的转换、“时间—测量值”数据表导出。
3.1 基本原理Matlab最初以数学计算为主,其提供的可视化技术,尤其是对计算结果的可视化处理是其一大特色,Matlab同时提供图像处理功能,图形工具从简单的点、线、面的处理发展到多维图形的表现。用户可以利用内部函数对外部图形进行操作,如:图形格式的转换、图形属性的实地调整、图形定制输出等,实现对图形深层次的控制,是Matlab语言在图形处理方面的强大体现(仵峰,2007)。
Matlab支持多种图像文件格式(王淑娟,2010),如:JPEG、TIFF、BMP、PNG、GIF等。图像在计算机中以数字方式存储与工作,换句话说,数字图像其实就是用数字信号来表示图像。数字图像相当于一个m×n的矩阵,也可以将数字图像形象比喻成一个m×n的网格,而一幅图像的每个网格则用一定颜色去填充,就形成我们所看到的完整图像(左飞,2014)。在Matlab中进行数字图像处理,主要通过使用图像处理工具箱提供的各种函数来实现,如图像的读取(imread)、写入(imwrite)、显示(imshow)及图像旋转(imrotate)等。
模拟记录中采用的记录图纸的时点轴线存在曲轴和直线轴2种,曲线矢量化后对不同的时点轴线应分别对待:①对于直角坐标所提取的曲线,当曲线起点时刻和终点时刻确定后,其间任意时点所对应的数值可在曲线上直接提取;②对于曲线轴而言,时点轴与记录曲线的交点值不能直接获取,需预先配置时点刻度线,然后求算时点刻度线与记录曲线的交点来获得对应时刻的观测值,获取观测值的时点间隔由使用者根据需要进行配置。
3.2 影像旋转在模拟纸带扫描中,不能使影像结果的横轴绝对水平,为此需将扫描影像旋转。Matlab具有图像旋转(imrotate)函数,扫描影像的旋转角度由功能模块完成,可依据图像上选择的任一水平轴线上具有较远距离的2点,计算横轴偏离水平的角度。如图 4,影像横轴偏离水平线(AA′)的角度α可以依据图中选择的A、B点影像的网格坐标(XA,YA)、(XB,YB),结合三角函数式计算,显然:tan(α) = (YB - YA)/(XB - XA),通过反正切函数计算角的弧度值,并转化为度,即为Matlab旋转函数需要的转角值。

|
图 4 影像旋转 (a)影像横轴偏离水平;(b)影像横轴旋转至水平 Fig.4 Image rotation |
部分Matlab代码如下
I=getimage; %获取打开的影像
a=ginput(2);%影像上选择水平轴线的两点
rotateA1=(a(3)-a(4))/(a(1)-a(2));
%计算影像水平轴线偏离水平的角度的正切值
rotateA2=atan(rotateA1);%获得角度的弧度值
Ang= rotateA2*180/(atan(1)*4);
%获得角度的度小数
imshow(imrotate(I, Ang, 'bicubic', 'loose'));
%对图像进行旋转,并显示结果图像
3.3 轴线匹配及曲线提取(1) 轴线匹配。对于轴线匹配,应针对影像纵轴是圆弧轴还是直线轴来进行轴线网格匹配。相对来说,直线轴匹配较为容易。对于圆弧轴线的匹配,需确定首条及最后一条圆弧轴线:通过首条圆弧轴线上2个轴线边点及轴线上任意一点,可确定圆弧轴线半径及对应圆心角(包括圆心角的起始方位和结束方位),从而确定首条圆弧轴;由于图像已旋转至水平,因此所有圆弧轴线的圆心纵坐标已知(同一图上的所有圆弧轴线的圆心纵坐标相同),通过最后一条圆弧轴线上任意一点确定该条圆弧轴线的圆心横坐标,而圆弧轴线所对应的圆心角及起始方位明确,因此可完成最后一条圆弧轴线匹配;当所需轴线的起点、终点明确后,根据起点时间与终点时间,即可按所需时间间隔分配区间的圆弧轴线。
(2) 曲线提取。曲线提取前需对所提取曲线的颜色进行取样,并对色彩提取阀值进行设置,当图像网格坐标处的色彩满足取样色的条件(存取该点的网格坐标)时,在影像图上进行曲线绘制,以展示所绘曲线是否满足原始曲线的趋势。影像上的轴线、曲线提取实例见图 5。
|
图 5 轴线及记录曲线提取 (a)曲线轴;(b)直线轴 Fig.5 Extraction of axes & record curve |
影像图表到实际图表设计思路是,首先获得轴线(时间线)与曲线(测量数值线)的交点坐标,此时时间线对坐标转换无意义,因为曲线与轴线的交点顺序为对应的时间点,所以图像坐标到实际坐标的转换,只需将图纸与图像的对应点进行匹配,匹配方法是:在计算机上获取2个清晰刻度点的图像纵坐标A、B,根据对应刻度线的实际值C、D进行纵轴值转换。图像上曲线任意一点图像纵坐标yi到实际纵轴值的计算式为
y = D + (yi -B)(C -D)/(A -B)或y = C + (yi -A)(C -D)/(A -B)
计算实例见表 1。
| 表 1 数值转换实例 Tab.1 Examples of numerical conversion |
获得相应时点测量值后,将“时点—测量值”输出到EXCEL,以方便分析预报人员进行数据共享、查寻和调用。
4 功能检验通过以上步骤即可完成模拟记录数据到数字化成果的转换。在此以2016年2月6日至7日模拟记录温度及2011年4月3日至4月4日模拟记录水位为例,对比同一模拟记录纸带矢量化后的重复读取结果(对同一幅记录纸带采用相同作业过程,进行2次自动读取获得观测值。其中涉及图像旋转、坐标轴匹配、取样色设置、影像坐标到实际坐标的转换,转换系数不一定完全相同),并对比自动读取与人工读取结果,以验证地震监测模拟记录图纸数字化的效果,具体对比结果见表 2 — 表 5。
| 表 2 模拟记录温度同一记录纸带2次自动读取结果对比 Tab.2 Comparison of two automatic reading values in terms of temperature |
| 表 3 模拟记录水位同一记录纸带2次自动读取结果比较(深度:m) Tab.3 Comparison of two automatic reading values in terms of water depth |
| 表 4 模拟记录温度的同一记录纸带自动读取与人工读取比较(温度:℃) Tab.4 Comparison of reading values in different ways in terms of temperature |
| 表 5 模拟记录水位的同一记录纸带的自动读取与人工读取比较(深度:m) Tab.5 Comparison of reading values in different ways in terms of water depth |
由表 2 — 表 5可知,通过以上2种模拟记录方式的记录图纸重复自动读取、自动读取与人工读取数值的比较不难看出:温度读取个别时点的测量值较差较大,如2016年2月7日8:00存在0.395℃的较差,通过图纸及影像分析,主要与模拟记录纸带上墨水笔画线的粗细和色彩浓度有关,但数据较差总体小于0.3℃,而在温度观测值的模拟图纸实际应用中,温度数值估读到±0.5℃;对于水位深度的读取,人工数值读取和矢量化水深曲线后自动提取数值的较差均不大于1 mm。因此,记录曲线矢量化后的曲线测量值与人工读取测量值具有一致性。
5 结束语地震模拟记录数字化对历史资料的有效保存及后续应用(共享、查询、分析)具有重要意义。通过对模拟记录曲线矢量化后自动获取观测值和人工读取观测值的对比,可知数据具有一致性,但数字化前应注意:①为了能够更加准确地自动获取各个时点所对应的模拟记录值,扫描的模拟记录图纸应具有清晰、可辨的色彩;②曲线的笔画不能太粗,且粗细应均匀;③对于历史既有资料,可能存在记录曲线线条粗细不均匀,曲线不够清晰可辨,造成数字化成果的“时点—测量值”不可靠,需人工读取予以修正。
| 孔月萍, 罗寅, 张跃鹏. 基于矢量化的山脉线提取方法[J]. 计算机工程, 2013, 39(3): 254-257. | |
| 石富强, 戴勇, 张博. 震例研究中前兆数据曲线快速矢量化程序[J]. 华北地震科学, 2015, 33(1): 57-60. | |
| 王淑娟, 张玉叶. 利用Matlab从图像中提取数据[J]. 科技信息, 2010(11): 49-50. DOI:10.3969/J.ISSN.1671-6027.2010.11.037 | |
| 仵峰. 用Matlab进行图形矢量化[J]. 中国农村水利水电, 2007(8): 31-33. | |
| 朱婧. 图像矢量化方法研究[D]. 杭州电子科技大学, 2011. | |
| 左飞. 数字图像处理[M]. 北京: 电子工业出版社, 2014. |
 2017, Vol. 38
2017, Vol. 38
