2. 中国北京 100029 中国地震局地质研究所
2. Institute of Geology, China Earthquake Administration, Beijing 100029, China
1966年邢台MS 6.8地震后,重力测量手段首次纳入地震前兆观测。随着重力测网的不断优化改造、重力观测仪器精度的不断提高以及观测技术的不断革新,重力测量已经成为地震前兆监测的重要手段之一(贾民育等,1996;曹建平等,2014;张永奇等,2014)。地震孕育过程中伴随着区域构造应力场的变化,地球深部物质的流动、地球介质的密度变化在地表会引起重力场变化(申重阳等,2001;申重阳,2005)。重力观测数据经过固体潮、气压、零点漂移、一次项等改正,可以获取监测区重力场随时间的非潮汐变化。一般认为,区域性重力场变化与大面积的降水、干旱、地下水开采、区域环境变化、地壳应变变化及深部物质运移等因素有关(陈石等,2011)。利用流动重力观测资料研究断裂活动引起的重力变化,对于揭示地质构造活动与地震之间的关系具有重要作用。近年来,利用重力资料对6级以上地震进行中短期预测预报取得较大进展(祝意青等, 2003, 2008),显示出重力手段对大震预测预报的优越性。
但是获取准确的重力场依赖于稳定可靠的起算基准,因此判定重力网起算基准的稳定性是一个重要环节。重力网平差一般采用3种方法:①自由网平差,该方法采用重心基准,假定所有重力点都是变化的,且变化等概率发生,如果网形不变,则起算基准相同,否则起算基准不同;②经典平差,该方法采用固定基准,假定测网中有已知重力值的起算基准;③拟稳平差,该方法采用拟稳基准,将测网的测点分为拟稳区和非拟稳区两部分,拟稳区的点相对于非拟稳区而言是稳定的(孙少安等,2012)。目前,数据解算基本采用经典平差和拟稳平差,由于拟稳平差涉及相对稳定点的选择,而该选择原则因人而异,存在较大偶然性,需要慎重选择。使用较多的是经典平差,只需选择一个稳定点相对容易,尤其是近年来在重力测网中加入绝对测量,使用经典平差方法更加有利。但经典平差假定每期重力观测起算点固定不变,与实际情况相悖(孙少安等,2009;李真等,2012;李真等,2013)。基于此,本文拟采用线性回归方法判定起算基准的稳定性,以获取更加可靠的重力点变化数据,为地震前兆研判提供准确的基础数据。
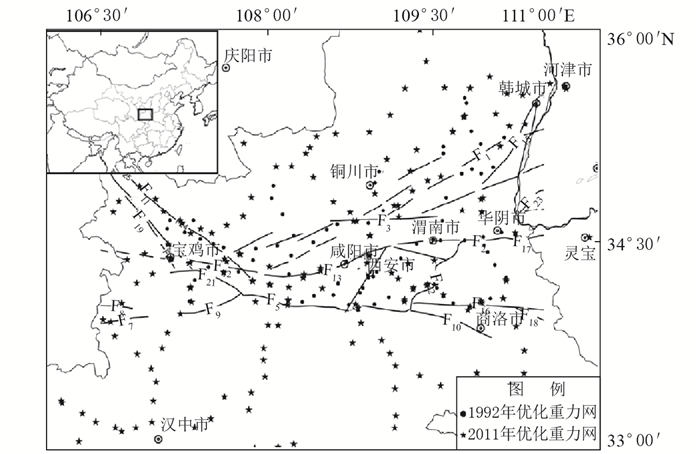
1 重力网概况及数据处理陕西重力测网也称“关中重力测网”,始建于20世纪80年代,随着重力监测技术进步和仪器精度的提高,原有重力测网无法满足高精度重力测量以及监测预报工作的需求(曹建平等,2014;张永奇等,2014),1991年进行优化改造,优化后的重力测网由11个闭合环、10条支线以及25个结点组成,共有131个测段、121个测点。随着城乡建设发展,部分测点被破坏,且监测范围有所调整,2011年再次对测网进行优化改造,改造后的重力测网基本覆盖整个陕西省,可对省内几条主要断裂进行有效控制,如:陇县—宝鸡断裂、渭河断裂、口镇—关山断裂、华山山前断裂、长安—临潼断裂等,具体点位分布见图 1。
|
图 1 陕西重力测网及主要断裂分布 Fig.1 The gravity network and the main fracture distribution of Shaanxi Province |
从1992年起,每年采用2台LCR-G型重力仪观测1期,观测时间一般为5 — 8月,2008年5月12日汶川MS 8.0地震后,从2009年起改为每年观测2期,第1期一般在3 — 4月完成,第2期在7 — 9月完成。采用中国地震局实用化攻关软件——LGADJ软件,对1992年以来重力网数据进行平差,平差采用三原测点作为起算基准进行经典平差,采用三原测点作为起算基准的原因是该测点位于测网的中部,减少测量误差传递的影响。具体计算步骤为:①首先对每一期的观测文件进行预处理,进行固体潮、仪器高、一次项、零漂、仪器格值等改正;②对多期重力资料计算结果进行整体分析,了解不同仪器的观测精度,以此确定各台仪器的先验方差,再进行整体平差,确保结果可靠。经统计每期观测点值精度均在15×10-8 m·s-2以内,解算结果可靠,统计结果见表 1。
| 表 1 各期观测资料精度 Tab.1 The precision of gravity observation data in each period |
自由网平差对测网要求严苛,实际上由于点位破坏及测网优化改造,网形几乎每年都变,因此陕西重力测网不适合采用自由网平差方法进行计算。经典平差要求选择测网中一个比较稳定的点,如果测网中有绝对测量点作为起算基准,效果更好(孙少安等,2012)。拟稳平差要求找到测网中相对稳定的一组测点,相对比较难实现。本文主要以经典平差为例进行基准稳定性分析。由于经典平差经常将起算基准赋于某一个固定值,然而测点的重力值随时间一直变化,因此会给整体解算带来系统误差(李真等,2012)。
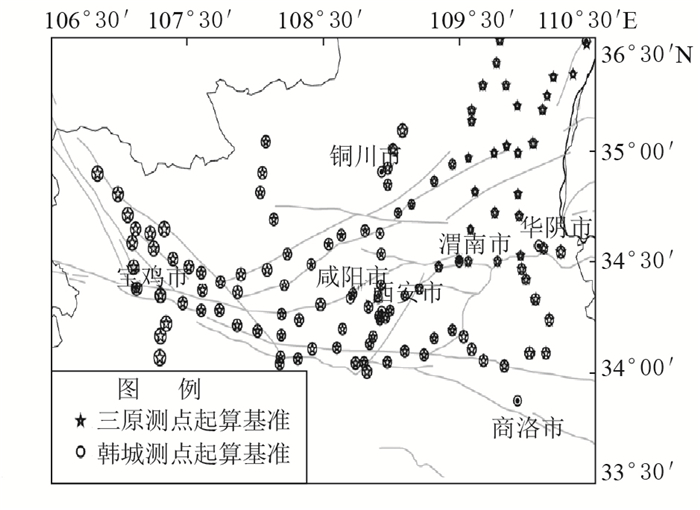
研究结果表明,测网测点整体平差精度与起算基准的位置有关,随着测点与起算基准距离的增加,测点的平差精度随之下降,表明起算基准的位置选择对整个测网平差精度起控制作用(李真等,2013)。因此,在选择起算基准时,尽量选择测网中心,即利用整个测网测点计算几何中心,在几何中心附近选择起算点。以1992年观测数据为例,采用位于测网中心的三原测点和测网东北角的韩城测点作为起算基准,分别统计测点平差精度。重力点值精度随起算基准距离的变化关系见图 2,基于不同起算基准点的测网精度见表 2。由图 2和表 2可知,三原测点周围测点精度较高,西部宝鸡地区和东部的渭南地区测点精度明显较差,而以韩城测点为基准的测点精度表明离起算基准测点越远测点精度越差,与李真等(2013)的研究结果一致。
|
图 2 重力点值精度随起算基准距离的变化关系 Fig.2 The relationship of gravity accuracy and distance from the datum point |
| 表 2 基于不同起算基准点的测网精度 Tab.2 The accuracy of gravity network based on the different datum |
重力网中任一点与起算基准点之间存在以下关系
| $ G_{m}^{n}=\Delta g_{m, 0}^{n}+G_{0}^{n} $ | (1) |
其中,
把1992年第1期重力网平差结果作为参考基准,也就是回归分析的自变量X0,其他各期平差结果作为因变量Yi,各期均以三原测点作为起算基准,并赋值为0,从而建立线性回归方程,即
| $ {{Y}_{i}}=A+B{{X}_{0}}\ \ \ \ \ (i=1, 2, \cdots, n) $ | (2) |
式中,假定残差resi= Yi - (A + BX0)服从平均值为0、方差为σ2i的正态统计分布,A、B可由最小二乘法确定,即利用残差平方和回归方程的斜率为
| $ B=\frac{\sum\limits_{i=1}^{n}{{{\omega }_{i}}({{X}_{0}}-\bar{X})({{Y}_{i}}-\bar{Y})}}{\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{({{X}_{0}}-\bar{X})}^{2}}}} $ | (3) |
式(3)表示2期观测数据之间的系统性差异及差值,随基准点的变化而变化,若X和Y的相关系数可以通过假设检验,则B具有实际意义(孙少安等,2009),其标准误差表示为
| $ {\rm{se}}(B)\sqrt{\frac{\sum\limits_{i=1}^{N}{{{\omega }_{i}}[{{({{Y}_{i}}-A+B{{X}_{0}})}^{2}}]}}{(N-2)\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{({{X}_{0}}-\bar{X})}^{2}}}}} $ | (4) |
线性回归方程的截距为
| $ A=\bar{Y}-B\bar{X} $ | (5) |
式(5)表示2期资料的不变性差异,即X和Y的基础性差值,与二者线性关系是否密切无关。也可以将截距理解为起算基准扰动,通过截距A可以改正其他每期的起算基准。其标准误差表示为
| $ {\rm{se}}(A)\sqrt{\frac{\sum\limits_{i=1}^{N}{{{\omega }_{i}}[{{({{Y}_{i}}-A+B{{X}_{0}})}^{2}}]}}{(N-2)}\left(\frac{1}{{{\omega }_{\rm{total}}}}+\frac{{\bar{X}}}{\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{({{X}_{0}}-\bar{X})}^{2}}}} \right)} $ | (6) |
线性回归方程整体拟合标准差表示为
| $ {\rm{SD=}}\sqrt{{\rm{RSS}}/(N-2)}=\sqrt{\sum\limits_{i=1}^{N}{{{\omega }_{i}}[{{({{Y}_{i}}-A+B{{X}_{0}})}^{2}}]/(N-2)}} $ | (7) |
拟合过程可使用每期误差si确定权重
当2个相互独立变量连续并服从正态分布,且存在线性关系,则可用相关系数检验其相关程度,一般R ≥(0.8 — 1.0)表示两变量间存在强相关。为验证2期数据采用线性回归拟合的可靠性,计算第1期与其他各期的相关系数R
| $ R=\frac{S{{X}_{0}}Y}{\sqrt{S{{X}_{0}}Y}\sqrt{SYY}}=\frac{\sum\limits_{i=1}^{n}{{{\omega }_{i}}({{X}_{0}}-\bar{X})({{Y}_{i}}-\bar{Y})}}{\sqrt{\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{({{X}_{0}}-\bar{X})}^{2}}}}\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{({{Y}_{i}}-\bar{Y})}^{2}}}} $ | (8) |
其中,式(3)—(8)中涉及的平均值及权重因子表达式如下
| $ \bar{X}=\frac{sx}{{{\omega }_{\rm{total}}}}=\frac{\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{X}_{0}}}}{{{\omega }_{\rm{total}}}}\ \ \ \ \ \ \ \ \bar{Y}=\frac{sy}{{{\omega }_{\rm{total}}}}=\frac{\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{Y}_{0}}}}{{{\omega }_{\rm{total}}}}\ \ \ \ \ \ \ \ {{\omega }_{\rm{total}}}=\sum\limits_{i=1}^{n}{{{\omega }_{i}}} $ |
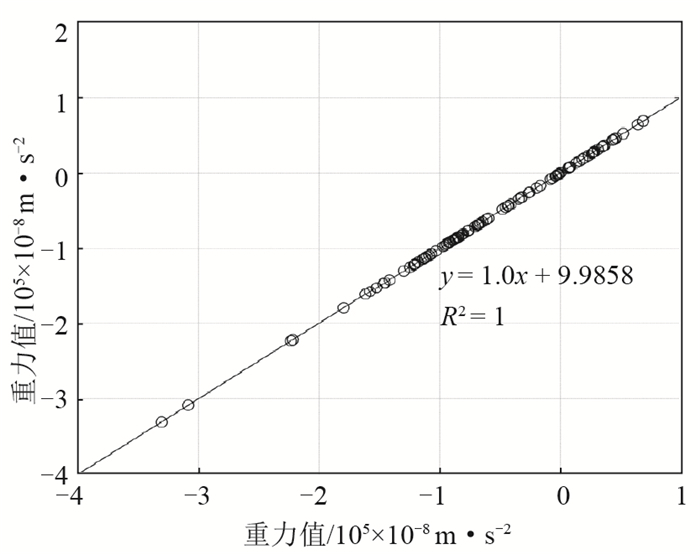
为了验证线性回归法的适用性,对1992年重力观测资料进行平差时,分别将起算基准三原测点赋值为0和10×10-8m·s-2,将平差结果作为线性回归方程的自变量和因变量,绘制图 3(横坐标起算点为0,纵坐标起算起点为10×10-8m·s-2)。从图 3可以看出,拟合效果较好,经计算相关系数R2 = 1。此外,截距9.985 8和初始输入的量值10×10-8 m·s-2相当,再次证明采用该方法进行起算基准稳定性分析的可靠性和有效性。
|
图 3 线性回归法有效性检验 Fig.3 The validity test of linear regression method |
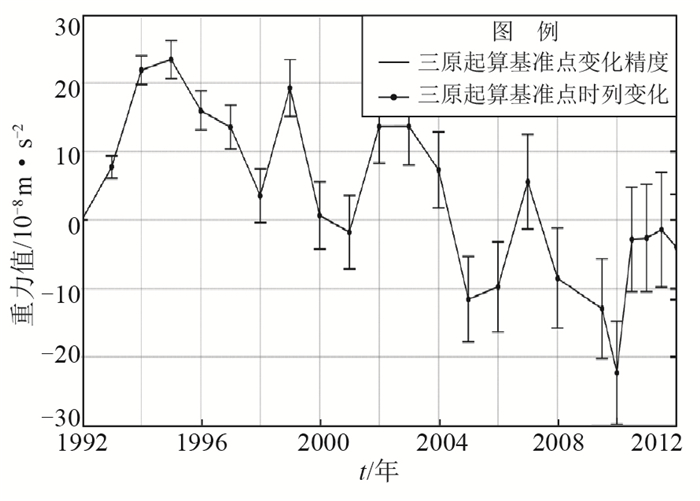
基于上述分析,对1992 — 2011年陕西重力网观测数据进行经典平差,平差基准以三原测点为起算基准,且赋值为0。将1992年重力网平差结果作为自变量,将1993 — 2011年数据作为因变量,进行线性回归拟合计算,计算结果见表 3、图 4。
| 表 3 回归系数及精度统计 Tab.3 Regression coefficient and its accuracy |
|
图 4 起算基准点(三原测点)时间序列变化 Fig.4 The time series of datum variation of gravity network(Sanyuan point) |
表 3中斜率基本为1,表明各期重力测量之间存在较强的线性关系,从相关系数也可以得到佐证。截距也就是各期起算基准的实际数值,为了消除由于起算基准引起的扰动,实际平差时根据表 3计算的截距结果,改变正负符号作为各期经典平差的起算基准值,从截距精度看,大部分精度优于起算基准变化量,但有几期精度较差,起算基准变化幅度基本在(-25 — 25)×10-8m·s-2。从图 4可以更直观了解三原起算基准的时序变化,总体上三原起算基准存在先正值变化后负值变化的规律,当起算基准点实际值高于零值而赋值为0,将使整个测网测点值偏低,相反,起算基准点实际值低于零值而赋值为0时,将使整个重力测网测点值偏高。
3 泾阳MS 4.8地震前后重力场变化在本文截取并计算的重力资料区间内,1998年1月5日在陕西泾阳发生MS 4.8地震(108°59′E,34°25′N),震中位于渭河断裂附近,属于左旋走滑性质的地震事件。为了进一步验证线性回归算法的有效性,本文以泾阳MS 4.8地震为例,从重力场和跨断层重力剖面变化两方面进行分析,以此说明线性回归算法在重力起算基准稳定性分析中具有积极的作用。
3.1 起算基准扰动改正前后重力场对比为了说明起算基准扰动引起的重力值变化幅度大小,可以计算起算基准扰动改正前后的重力值差值,首先推导引起重力场改正前后变化的公式,具体过程如下。假定2期重力变化如式(9)所示,即
| $ \Delta G={{G}_{n}}-{{G}_{m}}=\left(G_{n}^{b}-G_{n}^{a} \right)-\left(G_{m}^{b}-G_{m}^{a} \right)=\left(G_{n}^{b}-G_{m}^{b} \right)-\left(G_{n}^{a}-G_{m}^{a} \right) \\(m, n=1, 2\ldots, n>m) $ | (9) |
其中,ΔG表示2期重力值差值,Gma、Gmb表示第m期改正前、后重力值大小,Gna、Gnb表示第n期起算基准改正前、后重力值大小。由于第m、n期改正后的重力值可近似表示为
| $ G_{n}^{b}=G_{n}^{a}+\Delta {{g}_{n}}\ \ \ \ \ G_{m}^{b}=G_{m}^{a}+\Delta {{g}_{m}} $ | (10) |
其中,Δgm、Δgn表示起算基准变化量,将式(10)带入式(9),调整顺序后得
| $ \Delta G=\Delta {{g}_{n}}-\Delta {{g}_{m}} $ | (11) |
由式(11)知,根据2期重力值计算的重力场变化,实际是由起算基准扰动变化引起的,因此某期起算基准扰动大,就会对重力场变化产生较大影响。为了直观体现改正前后重力场变化情况,绘制重力场差值等值线图,限于篇幅,本文只列出1995 — 2000年重力数据计算的重力场变化结果,见图 5。
|
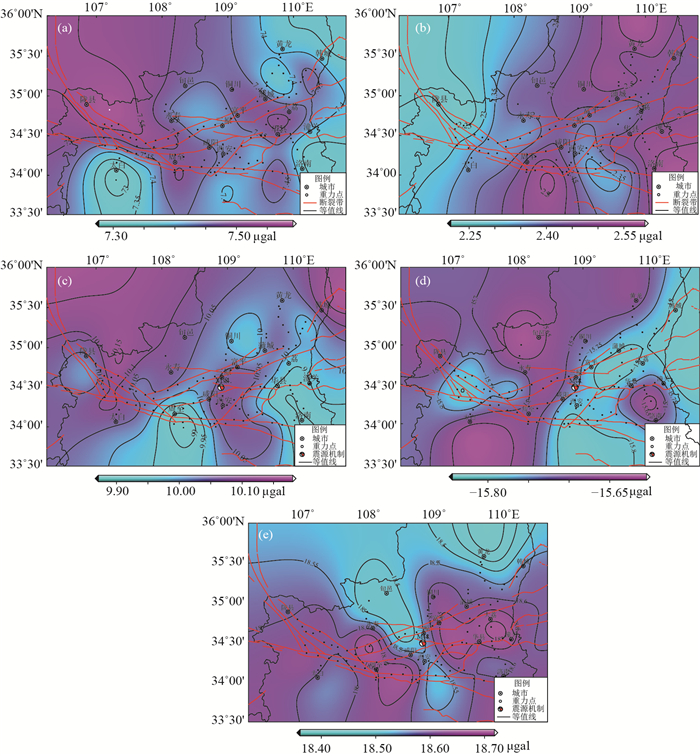
图 5 起算基准改正前后重力场变化 (a)1995年7月— 1996年7月;(b)1996年7月— 1997年7月;(c) 1997年7月— 1998年10月;(d) 1998年10月— 1999年7月;(e) 1999年7月— 2000年7月 Fig.5 The gravity variation before and after correcting the datum |
图 5(a)显示,起算基准改正前后重力场变化基本在(7.25 — 7.6)×10-8 m·s-2,变化较大区域在关中西部,中东部变化相对较小,该期改正值与测网后验中误差量值相当。图 5(b)显示,起算基准改正前后重力场变化基本在(2.2 — 2.6)×10-8 m·s-2,变化较大区域在关中中东部,西部变化相对较小,该期改正值小于测网后验中误差量值。图 5(c)显示,起算基准改正前后重力场变化在(9.85 — 10.2)×10-8 m·s-2,变化较大区域为关中西部和此次泾阳MS 4.8震中附近,该期改正值略大于测网后验中误差量值。图 5(d)显示,起算基准改正前后重力场变化在(-15.85 — 15.6)×10-8 m·s-2,变化较大区域为关中东部,关中西部变化相对较小,该期改正值接近于2倍测网后验中误差量值。图 5(e)显示,起算基准改正前后重力场变化在(16.35 — 16.7)×10-8 m·s-2,关中地区变化较大,关中北部变化相对较小,该期改正值接近于2倍测网后验中误差量值。从图 5可以看出,有的期次起算基准改正前后重力场变化相对较大,对可靠获取重力场图像具有比较明显的影响,在实际分析过程中需要考虑起算基准的扰动影响。
3.2 地震前后重力场变化为了进一步检验线性回归方法的有效性,利用改正后新的起算基准进行经典平差,绘制研究区1995 — 2000年重力场变化图像,见图 6。

|
图 6 泾阳MS 4.8地震前后重力场变化 (a)1995年7月— 1996年7月;(b)1996年7月— 1997年7月;(c)1997年7月— 1998年10月;(d)1998年10月— 1999年7月;(e)1999年7月— 2000年7月 Fig.6 The gravity variation before and after the Jingyang MS 4.8 earthquake |
从图 6(a)可以看出,1995年7月— 1996月7月关中地区重力场变化幅度不大,基本在(-25 — 35)×10-8 m·s-2,以宝鸡—永寿—泾阳—大荔一线为界,其北部表现为大范围重力场正值变化,南部表现为大范围负值变化。泾阳处于零值线附近。图 6(b)显示,1996年7月— 1997年7月重力场相比上期出现反向变化,关中北部地区重力场以负值变化为主,南部以正值变化为主,变化范围为(-25 — 40)×10-8 m·s-2,零值线走向为NW—SE,与渭河盆地几条断裂斜交。最大的重力场正向变化分布在太白以南,最大负向变化分布在黄龙以北。图 6(c)(1997年7月— 1998年10月)显示,泾阳震源区出现小幅的重力场正值变化,变化幅度15×10-8 m·s-2,而西部大范围地区重力场以负值变化为主,尤其是陇县、太白以西,重力场负值变化达到-60×10-8 m·s-2。图 6(d)显示,1998年1月5日泾阳MS 4.8地震后,震源区出现由北向南的较大范围的重力场负值变化区,东、西部出现大范围重力场正值变化区。图 6(e)显示,地震之后2年,震源区重力场变化格局基本恢复到震前两年的形态,差别在于震前两年零值线走向为NE—SW,震后2年零值线走向为NW—SE。
分析图 6可知,经过起算基准变化改正后,重力场变化特征更加明显,孕震过程符合扩容理论,而重力场异常变化不明显,与地震震级偏低有关。总之,经过起算基准改正的重力场变化图像更符合实际情况,可为进一步研究重力场变化与地震的关系提供更加准确、真实的基础资料。
3.3 跨断裂段差时序分析为了更好了解泾阳MS 4.8地震前后震中附近断裂活动情况,利用起算基准改正后计算的1995 — 2000年段差数据,进行跨断裂重力段差时间序列分析。限于篇幅,本文只分析此次震中附近几条断裂重力段差变化(上盘相对于下盘),并绘制跨断裂重力段差时序变化曲线,见图 7。
|
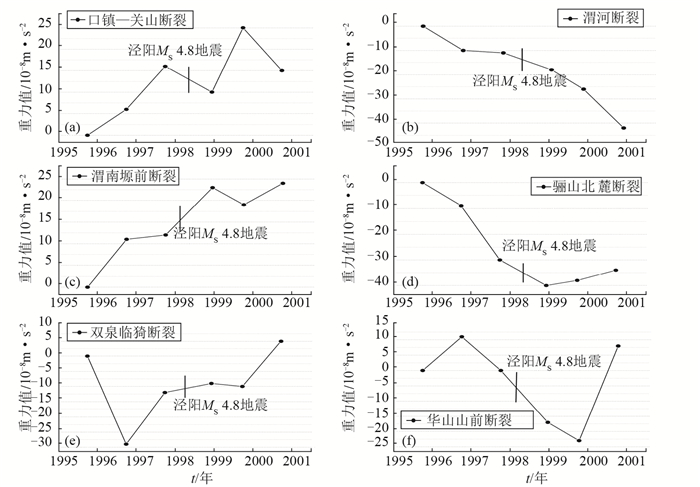
图 7 跨断裂重力段差时间序列变化 Fig.7 The time series change of gravity segment difference crossing the faults |
由图 7(a)可知,1998年1月5日泾阳MS 4.8地震前,跨口镇—关山断裂的重力段差出现加速上升变化,在转为下降变化时发生地震,震后转为上升变化,呈现波动型变化;由图 7(b)知,泾阳MS 4.8地震前后跨渭河断裂的重力段差一直是负向变化,1995年7月— 2000年7月累积变化达到40×10-8 m·s-2左右;从图 7(c)知,跨渭南塬前断裂的重力段差在泾阳MS 4.8地震前表现为加速上升—缓慢上升—加速上升,在上升变化过程中发生地震,地震之后出现小幅下降变化,然后继续上升变化。从图 7(d)知,跨骊山北麓断裂的重力段差在泾阳MS 4.8地震前加速下降,在下降过程中发震,震后转为小幅上升变化。从图 7(e)知,跨双泉—临猗断裂的重力段差在泾阳MS 4.8地震前出现大幅下降变化,在转为上升变化的过程中发生地震,震后小幅下降之后出现大幅上升变化。从图 7(f)知,跨华山山前断裂的重力段差在泾阳MS 4.8地震前表现为上升—下降—加速下降,在加速下降过程中发生地震,之后是小幅下降—大幅上升。
从图 7可知,大部分跨越断裂的重力段差在其下降变化过程中发生地震,如跨越口镇—关山断裂、渭河断裂、渭河北麓断裂和华山山前断裂的重力段差变化都属于这种情况;而跨越渭南塬前断裂和双泉—临猗断裂的重力段差变化,地震却发生在其上升过程中。从震中位置看,泾阳MS 4.8地震发生在渭河断裂、口镇—关山断裂、渭南塬前断裂附近,重力段差变化的差异性表明,表明此次地震受到不同断裂相对复杂运动的影响。
4 结论(1) 重力网平差时,起算基准选择比较关键,若测网存在多个绝对基准点,宜采用拟稳平差方法;若测网无绝对测量点,采用经典平差法比较适合。由于任何重力测点都非恒定不变,因此在采用单测点进行经典平差时,需对起算基准的扰动进行改正。另外,起算点的位置与整体平差精度相关,测点离起算点越远,精度越差,因此需要选择测网几何中心附近的点作为起算基准点。
(2) 线性回归拟合法进行起算基准稳定性分析,效果较好,可以作为一种行之有效的起算基准改正方法,从而获取起算基准的时序变化值。从起算基准改正前后的重力场差异变化看,在分析实际重力场时必须进行起算基准扰动改正。
(3) 通过分析1998年1月5日泾阳MS 4.8地震前后重力场变化及跨断裂重力段差时序变化,发现起算基准扰动改正后,变化特征更加符合真实的重力变化规律。
感谢审稿专家及编辑同志提出的建设性修改意见,对文章质量的提升大有益处。在文章撰写过程中与中国地震局地球物理勘探中心的李真工程师进行了多次有益讨论,在此一并感谢。| 曹建平, 祝意青, 韩美涛, 等. 陕西重力网优化改造及监测能力评估[J]. 地震地磁观测与研究, 2014, 35(1/2): 165-170. | |
| 陈石, 祝意青, 蒋长胜, 等. 新疆于田MS7.3地震前重力场变化的质源体特征[J]. 地震地磁观测与研究, 2011, 32(5): 1-8. | |
| 贾民育. 滇西动态重力网的分形特征及空间分辨率[J]. 地壳形变与地震, 1996, 16(4): 26-30. | |
| 贾民育, 詹洁晖. 中国地震重力监测体系的结构与能力[J]. 地震学报, 2000, 22(4): 360-367. | |
| 李真, 秦建增, 陈石. 山西地震重力监测网起算基准扰动分析[J]. 地震, 2013, 33(3): 60-66. | |
| 李真, 陈石. 多网重力数据联合平差和系统误差改正[J]. 地震, 2012, 32(2): 95-103. | |
| 申重阳, 吴云, 甘家思. 从地壳运动角度分析大陆强震机理的一种物理方法[J]. 中国地震, 2001, 17(1): 70-81. | |
| 申重阳. 地壳形变与密度变化耦合运动探析[J]. 大地测量与地球动力学, 2005, 25(3): 7-12. | |
| 孙少安, 康开轩, 黄邦武. 关于区域重力场变化基准的思考[J]. 大地测量与地球动力学, 2012, 32(1): 17-20. | |
| 孙少安, 项爱民, 周新. 龙门山区域重力网起算基准扰动分析[J]. 大地测量与地球动力学, 2009, 29(6): 8-12. | |
| 张永奇, 曹建平, 郝洪涛, 等. 陕西地区流动重力历史资料清理分析[J]. 地震地磁观测与研究, 2014, 35(1/2): 171-176. | |
| 祝意青, 王双绪, 江在森, 等. 昆仑山口西8.1级地震前重力变化[J]. 地震学报, 2003, 25(3): 291-297. | |
| 祝意青, 徐云马, 梁伟锋. 2008年新疆于田MS7.3地震的中期预测[J]. 大地测量与地球动力学, 2008, 28(5): 13-16. | |
| 祝意青, 梁伟锋, 徐云马. 重力资料对2008年汶川MS8.0地震的中期预测[J]. 国际地震动态, 2008(7): 36-39. |
 2017, Vol. 38
2017, Vol. 38

 ,
,