2. 中国山西 030025 太原大陆裂谷动力学国家野外科学观测研究站
2. National Continental Rift Valley Dynamics Observatory of Taiyuan, Shanxi Province 030025, China
地震预警构想(Cooper J D,1868)最早由美国的Cooper博士在1868年针对美国旧金山市提出,他设想在距离旧金山市约100 km的Hollister地区(当时地震活动非常剧烈)布设地震监测装置,利用电磁波比地震波传播快的原理,在震后通过电磁波及时敲响市政大楼上的大钟,发出地震警报。地震预警的具体思想(马强,2008)是,利用布设在预警目标区或潜在震源区的地震台网或强震台网以及实时通信传输线路,对地震进行实时监测,利用地震P波传播速度大于破坏性S波和面波以及电磁波速远大于地震波速的原理,在尽可能短的时间内确定地震基本参数(震源位置、发震时刻、地震震级)或直接估计预警目标区地震动和破坏程度,进而抢在地震P波或强地面运动段S波到达预警目标区之前,对可能破坏区发出地震警报,并启动地震应急控制系统,警告人们撤离危险场所,快速列车减速或停止,关闭煤气等危险源,停止某些生产过程,如高空作业等,以消除潜在威胁,减少伤亡等。
目前,国际上许多地震预警系统已经取得减灾实效,如:日本紧急地震速报预警系统(Kamigaichi O,2004)、美国ElarmS系统(Allen R M et al,2003)、墨西哥SAS系统(Espinosa-Aranda J M et al,1995)、中国台湾地区速报及预警系统(Wu Y M et al,1999)、土耳其伊斯坦布尔市预警系统(Erdik M et al,2003)、罗马尼亚地震预警系统(Ionescu C et al,2006)等。中国目前在积极开展地震预警有关工作,包括:2013年6月验收的“地震预警与烈度速报系统的研究与示范应用”国家科技支撑计划,已经完成立项的“国家地震烈度速报与预警工程”(杨陈等,2015)。
“山西国家地震烈度速报与预警工程”台站勘选工作于2016年1月启动,2016年5月1 101个预警台站勘选工作结束。本文将结合山西地区历史地震及断层分布,对山西地震台网未来1 101个预警台站平均台间距和盲区半径分布进行分析,以期对山西预警台网的台站布局有初步了解,为“山西国家地震烈度速报与预警工程”项目的后续工作提供参考。
1 地震预警关键技术指标 1.1 预警时间预警时间是指,对指定位置发布地震预警的时间与即将到达的地面震动间的时间差。因此,震中距、数据传输延时、地震参数确定时间、处理发布时间均会影响预警时间(Kuyuk H S et al,2013;杨陈等,2015)。
1.2 预警盲区震中周围可能存在一部分区域,因强震动在预警时间内发生,而不能提供地震预警,此区域即为预警盲区,是以震中为圆心、以预警时间内S波传播距离为半径的圆(杨陈,2013)。
提高地震预警系统效能的一个关键问题是使地震预警盲区最小。地震预警盲区大小与预警时间长短息息相关,可以通过降低传输延时、提高数据打包速度、改进预警定位算法、完善地震台网布局等减小预警盲区。因不同地震预警系统的反应时间不尽相同,且预警定位方法和计算机处理发布技术不断改进,故本文只讨论地震台间距对预警盲区的影响。
预设地震预警系统采用简单双台预警模式,估算台间距对预警盲区的影响,假设地震发生在2个地震台站连线中间,暂不考虑系统反应时间,则盲区半径R0与台间距L的关系(杨陈,2013;杨陈等,2015)为
| $ {{R}_{0}}=\sqrt{{{\left[ \ {{v}_{\text{S}}}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}} \right) \right]}^{2}}-{{h}^{2}}}=\sqrt{{{\left[ \ {{v}_{\text{S}}}\left( \frac{\sqrt{\frac{{{L}^{2}}}{4}\text{+}{{h}^{2}}}}{\ {{v}_{P}}}+{{t}_{2}}+{{t}_{3}} \right) \right]}^{2}}-{{h}^{2}}} $ | (1) |
式中:t1为P波初至走时,t2为P波截取时长,t3为传输延时、处理发布用时,vS为S波速度,vP为P波速度,L为台间距,h为震源深度。
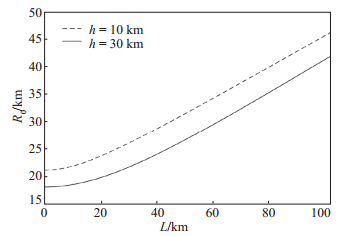
取t2 = 3 s,t3 = 2 s,vS =3.5 km/s,vP = 6.0 km/s,对于h =10 km、30 km,根据式(1)绘制地震台间距L与盲区半径R0的关系图(图 1)。由式(1)及图 1可知,L= 0对应盲区半径最小,即h =10 km时,R0 = 21.08 km,h =30 km时,R0 = 18.03 km;当台间距L<10 km时,盲区半径R0随L的减小不明显,即当台间距小到一定程度,继续加密地震台网,对缩小预警盲区范围作用不大;当L>20 km时,盲区半径R0随L的增加几乎呈线性增长。可见,10 km和20 km是台间距的2个临界值,且从图 1中2条不同震源深度的对比曲线可知,在台间距相同前提下,震源较深的地震所对应的盲区半径较小。
|
图 1 盲区半径R0与台间距L的关系 Fig.1 Relationship between blind-zone radius R0 and interstation distance L |
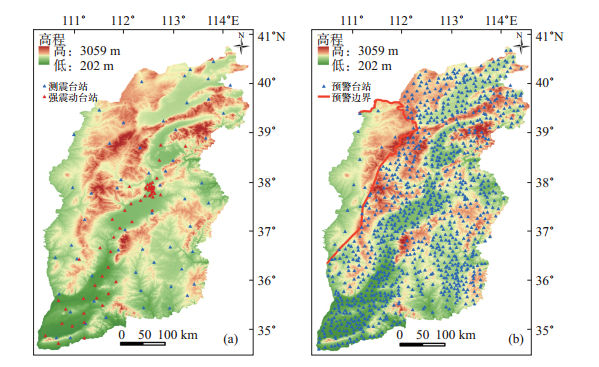
目前,山西省地震监测台网由1个省级测震台网和3个地方测震台网组成,涵盖57个测震台站。根据地震活动性,山西省强震动台站主要分布在忻定盆地、太原盆地、临汾盆地和运城盆地范围内,目前正常运行的强震动台站共计56个,测震台站和强震动台站分布见图 2(a)。
|
图 2 山西地震台网测震台站和强震动台站及预警台站分布 Fig.2 Distributions of seismic and strong motion stations in Shanxi Seismic Network and warning stations |
在山西国家地震烈度速报与预警工程项目中,预警台站规模较大,拟设置1 101个预警台站。其中,山西地震台网的57个测震台站中有51个台站作为改造基准站,56个强震动台站中有32个台站作为改造基本站,5个背景场项目中建设的强震动台站作为在建基本站,新建30个基准站、122个基本站和861个一般站。山西省1 101个预警台站分布见图 2(b),图中红色线条以东为预警区,以西为非预警区。
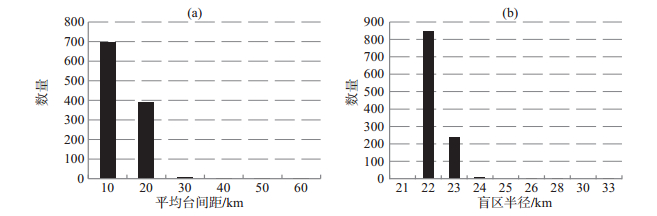
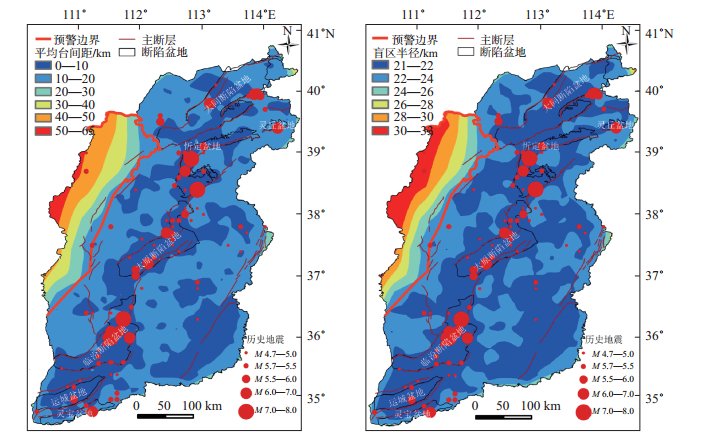
根据山西省面积和拟设置的1 101个地震预警台站,得出未来山西省地震预警台网密度为每万平方千米70.26个台站,以每个台站到最近3个台站的距离求平均(Kuyuk H S et al,2013),计算得到全省平均台间距为9.62 km,假设震源深度为10 km,根据式(1),计算得到相应盲区半径,见图 3。统计山西地区历史上发生的M > 4.7地震,绘制该省主要断层及断陷盆地与1 101个预警台站平均台间距分布及盲区半径分布叠加图,见图 4。
|
图 3 台间距及盲区半径统计 Fig.3 Statistical histograms of interstation distance and blind-zone radius |
|
图 4 山西省主要断层、盆地及M>4.7历史地震分布与平均台间距及盲区半径分布对比 Fig.4 Comparisons of the interstation distanceand blind-zone radius of Shanxi Seismic Networkand the main faults、basins and the M > 4.7 earthquakes |
由式(1)可得,当台间距L=10 km、20 km临界值时,对应盲区半径R0分别为21.8 km、23.7 km。由图 3可知,山西省预警台站平均台间距集中在10 km和20 km,98.91%的地震台站平均台间距小于20 km,盲区半径集中在22 km、23 km;99.18%的地震台站对应盲区半径小于24 km;从图 4可以看出,山西省平均台间距10 km以内和盲区半径22 km以内区域基本覆盖该省主要盆地、断层及历史地震活动密集区,且在地震预警区内,台间距基本小于20 km,盲区半径基本小于24 km。由此可见,山西地震预警台站平均台间距及盲区半径分布比较合理。
3 结论地震预警时间和台间距密切相关,因此应根据特定区域地震特点布设地震台站。在断层分布及历史地震活跃区域,尤其是人口密集和经济发达地区,台站应较密集布设,降低平均台间距,从而提高这些区域在地震到来时可用的预警时间,而在其他区域选择合理台间距进行台站布设。根据图 1可知,台间距在0—10 km范围内对应的盲区半径变化不明显,而当台间距大于20 km时,对应的盲区半径变化较快。因此,在已知危险性断层区域及靠近断层的城市人口密集区,目标台间距10 km较为合理;在距离危险性断层较远及远离人口密集区域,目标台间距在20 km左右较为合理。
根据勘选完成的山西地震台网1 101个地震预警台站布局,假设采用简单的双台预警模式,处理及传输时间为2 s,在震源深度为10 km时,山西省地震盲区最小半径约为21 km。由图 3和图 4可知,在地震预警区内,大同断陷盆地、忻定盆地、太原断陷盆地南部、临汾断陷盆地及运城盆地等区域以及历史地震活跃区域的平均台间距控制在10 km以内,盲区半径控制在22 km以内;吕梁地区和晋中地区这些隆起区域的平均台间距控制在20 km以内,盲区半径控制在24 km以内。因此,目前山西省1 101个地震预警台站总体布局较为合理,平均台间距及盲区半径分布与地震活动的相关性较高。如果能缩短数据处理时间及传输延时,山西省预警盲区半径将会相应减小。
| 马强. 地震预警技术研究及应用[D]. 哈尔滨: 中国地震局工程力学研究所, 2008: 2-8. http://d.wanfangdata.com.cn/Thesis/Y1597107 | |
| 杨陈. 中国地震预警系统建设的几个关键问题[J]. 工程研究——跨学科视野中的工程, 2013, 5(4): 354-364. | |
| 杨陈, 郭凯, 张素灵, 等. 中国地震台网现状及其预警能力分析[J]. 地震学报, 2015, 37(3): 508-515. DOI:10.11939/j.issn:0253-3782.2015.03.013 | |
| Allen R M, Kanamori H. The potential for earthquake early warning in southern California[J]. Science, 2003, 300(5 620): 786-789. | |
| Cooper J D. Letter to editor[N]. San Francisco Daily Evening Bulletin, 1868-11-03(23). | |
| Erdik M, Fahjan Y, Ozel O, et al. Istanbul earthquake rapid response and the early warningsystem[J]. Bulletin of Earthquake Engineering, 2003, 1(1): 157-163. DOI:10.1023/A:1024813612271 | |
| Espinosa-Aranda J M, Jiménez A, Ibarrola G, et al. Mexico City seismic alert system[J]. Seismological Research Letters, 1995, 66(6): 42-53. DOI:10.1785/gssrl.66.6.42 | |
| Ionescu C, Marmureanu A. Vrancea rapid early warning system (REWS) for Bucharest and industrial objectives-new technology for earthquakes monitoring[J]. Acta Geodaetica et Geophysica Hungarica, 2006, 41(3/4): 349-359. | |
| Kamigaichi O. JMA earthquake early warning[J]. Journal of Japan Association for Earthquake Engineering, 2004, 4(3): 134-137. DOI:10.5610/jaee.4.3_134 | |
| Kuyuk H S, Allen R M. Optimal seismic network density for earthquake early warning:a case study from California[J]. Seismological Research Letters, 2013, 84(6): 946-954. DOI:10.1785/0220130043 | |
| Wu Y M, Chung J K, Shin T C, et al. Development of an integrated seismic early warning system in Taiwan-case for Hualien earthquakes[J]. Terrestrial, Atmospheric and Oceanic Sciences, 1999, 10(4): 719-736. DOI:10.3319/TAO.1999.10.4.719(T) |
 2017, Vol. 38
2017, Vol. 38
