2. 中国西安 710068 陕西省地震局
2. Shaanxi Earthquake Agency, Xi'an 710068, China
震源深度是地震时空基本参数之一,在发震构造、应力场和地震危险性评估研究等方面具有重要作用。目前,震源深度是震源参数中最难准确测定的参数之一。受地震台站包裹性、定位方法等影响,在地震定位过程中震源深度存在一定误差。利用深度震相来确定震源深度,可以提高地震定位精度。
在同一震源深度上,不同震中距的深度震相与其参考震相的到时差几乎不变,这一特点使得利用深度震相来计算震源深度成为可能(龙锋等,2014)。对于地壳结构相对简单的区域,近震深度震相sPg、sPmP和sPn及其参考震相Pg、PmP和Pn,在近震波形上可以清楚观测到,通过测量不同震相之间的到时差或通过波形对比方法,可以获得较为精确的震源深度。国内外许多学者就此开展了不少研究(Saikia C A,1987;Bock G et al,1996;Langston C K,2000;任克新等,2004;魏娅玲等,2013)。但上述深度震相一般有其优势的震中范围和使用条件。海南省是少震弱震地区,受地理位置限制,地震台站只能分布在岛陆上,一般难以记录到上述深度震相。崇加军等(2010)提出1种新的近震深度震相sPL,该震相通常在震中距50 km范围内,在地壳结构相对简单地区可以明显观测到。詹小艳等(2014)利用sPL震相确定了江苏高邮M 4.9地震震源深度,项月文等(2014)利用sPL震相确定了九江—瑞昌MS 5.7地震序列震源深度,结果表明,利用sPL震相确定震源深度是可靠的。海南测震台网记录到一些空隙角大的小地震,用同一种定位方法参与定位的震相到时不变,有时会给出不同震源深度,相差甚至达上百千米。利用sPL震相定位震源深度,只要有1个地震台站记录,就可以比较准确地定位震源深度。在地震台网相对稀疏或地震台布局不太合理的情况下,用sPL震相确定震源深度具有一定意义。
据海南地震台网测定:2014年7月28日10时10分,在海南儋州市发生2.6级地震,震中位于(19.64°N,109.58°E),震源深度16 km。本文采用海南数字测震台网记录的此次地震波形数据,利用sPL震相,重新测定震源深度。
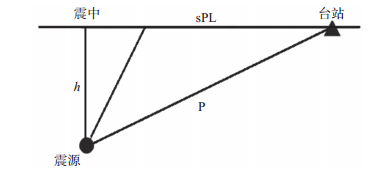
1 sPL震相特征及走时方程sPL震相是指,从震源出发的SV波入射到自由表面下方时,将一部分能量转换为P波,当临界入射时,转换P波沿地表传播,或在浅层(如盖层)的一系列多次反射或转换震相(崇加军等,2010)。sPL震相水平视速度与P波速度相等,一般在震中距50 km范围内发育较好。在宽频带地震记录中,通常在直达P波之后、S波之前可能观测到该震相,随距离变化衰减快,但起始可能比直达S波尖锐,某些方面具有与首波类似的性质(Aki K et al,2002)。sPL震相基本特征是:能量主要集中在径向分量,垂向分量振幅相对径向分量小,切向分量振幅较弱,几乎为零,波形具有低频特性,所含高频成分相对较少,没有P波尖锐(崇加军等,2010)。传播路径见图 1。
|
图 1 均匀半空间下sPL、直达P波传播路径 Fig.1 Ray path of sPL and P wave for the model half space |
根据均匀半空间模型sPL震相产生原理(崇加军等,2010),设P波速度为vP,已知vP/vS波速比为α,震源深度为h,则sPL、P波震相到时差tsPL-P与震中距Δ的关系(包丰等,2013)可表示为
| $ {t_{{\rm{sPL - P}}}} = \frac{{h \times \sqrt {{\alpha ^2} - 1} + \Delta - \sqrt {{h^2} - {\mathit{\Delta }^{\rm{2}}}} }}{{{v_{\rm{P}}}}} $ | (1) |
若h2≪Δ2,即h2 + Δ2的值趋于Δ2,则式(1)近似为
| $ {t_{{\rm{sPL - P}}}} = \frac{{\sqrt {{\alpha ^2} - 1} }}{{{v_{\rm{P}}}}} \times h $ | (2) |
由式(2)可以看出,tsPL-P与震中距关系不大,而随震源深度增加几乎呈线性增加,利用此特征可以很好地约束震源深度(崇加军等,2010)。震中距较小的地震台站能较清晰地记录到sPL震相。一般震中距50 km范围内的地震台,记录的地震波形通常具有较高信噪比,出现的震相较少,直达P波和S波之间一般只会存在sPL震相,所以sPL震相不易与其他震混淆。因此,在地震台站布局稀疏或不合理情况下,可以用近台记录的sPL震相较精确地确定较小地震的震源深度。
2 PL震相识别及震源深度确定 2.1 地震数据一般sPL震相在震中距50 km范围内比较容易被清晰观测到,2014年7月28日10时10分在海南儋州市发生的2.6级地震震中距条件符合,该地震被3个地震台站记录到,即松林岭台(SLL)、临高台(LIG)和澄迈台(CHM)。其中,临高台(LIG)未记录到sPL震相,澄迈台(CHM)记录到此震相,但由于数据波形质量不理想,不予采用。因此,采用松林岭台(SLL)宽频带测震台站记录,震中距24 km,方位角320°,带宽50 Hz—60 s,地震计CMG-3ESPC-60,数采TDE-324CI。
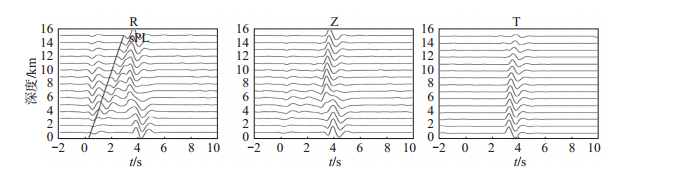
2.2 sPL震相识别将地震波形数据SEED格式转换成SAC格式,对地震台站数据去除场地响应,并挑选震中距小于60 km的3个地震台站:松林岭台(震中距24 km)、临高台(震中距26 km)和澄迈台(震中距40 km),对各台站地震数据进行预处理,步骤为:标注直达P波和S波的震相到时,将水平分向旋转至径向和切向,采用1 Hz以下低通滤波,积分至地表位移。结果发现,松林岭台直达P波与S波之间记录到一清晰震相,见图 2(图中黑色曲线代表径向分量R,红色代表切向分量T,绿色代表垂直向分量Z):①震相径向分量振幅最大,垂直分量次之,切向分量较弱;②震相起始没有P波尖锐。根据以上记录的震相特征和松林岭台的震中距,结合sPL震相基本特征,判定该震相为sPL震相。

|
图 2 sPL震相识别 Fig.2 Identification of sPL phase |
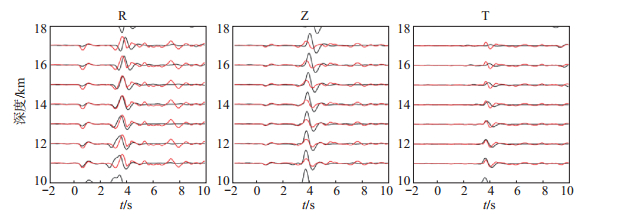
采用P波初动法反演得到海南儋州地震的震源机制解(截面Ⅰ:走向68°,倾角44°,滑动角172°;截面Ⅱ:走向163°,倾角85°,滑动角47°),任选一个节面作为断层面。采用F—K方法,在不同震源深度(1—15 km)下,合成松林岭台记录的径向、垂直向和切向理论波形,见图 3,不难看出,随着震源深度的增加,sPL和P波震相到时差呈线性增大,与公式(2)相吻合,由此可以利用实际波形与理论波形拟合对比来约束震源深度。
|
图 3 SLL台不同震源深度径向、垂直向、切向理论波形 Fig.3 The radial, vertical and tangential theoretical waveform of different depth at SLL station |
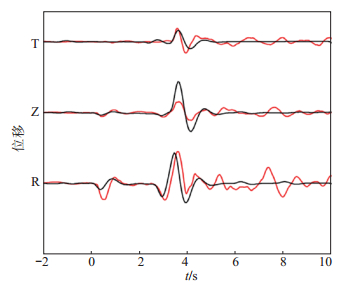
地震数据预处理后,将实际波形与不同震源深度下理论波形进行拟合,见图 4(图中黑色曲线代表理论波形,红色曲线代表实际波形),拟合原则是,sPL和P波震相相对到时吻合较好。从图 4可以看出,震源深度在14 km处,松林岭台三分量上的P波和sPL震相相对到时拟合较好。
|
图 4 SLL台不同震源深度实际波形与理论波形拟合 Fig.4 The actual waveform and theoretical waveform of different depth fitting at SLL station |
对震源深度14 km处该台实际波形和理论波形进行拟合,见图 5(图中黑色曲线代表理论波形,红色曲线代表实际波形),可见直达P波、S波的实际波形与理论波形吻合较好,sPL震相在直达波P和S波之间出现,在径向和垂直向sPL震相实际波形与理论波形拟合较好,在切向未出现sPL震相。其能量主要分布在径向,垂直向较小,而切向较弱,几乎看不到。因此认为,海南儋州地震的震源深度约14 km。与海南测震台网地震编目给出的地震震源深度16 km,及采用PTD法(朱元清等,1990)给出的震源深度13.1 km相差不大,在误差允许范围内。用sPL震相确定震源深度也存在一定误差,主要由震相读数误差、地壳速度模型等(崇加军等,2010;项月文等,2014)造成,误差约为真实震源深度的10%。
|
图 5 震源深度14 km处SLL台实际波形与理论波形对比 Fig.5 The contrast figure of actual waveform and theoretical waveform of 14 km depth at SLL station |
通过对海南测震台网记录的2014年7月28日海南儋州2.6级地震波形数据进行预处理。根据sPL震相波形特征,发现松林岭台(SLL)记录到sPL震相。利用F—K方法合成的不同震源深度sPL震相理论波形,通过波形拟合对比,确定此次2.6级地震的震源深度约14 km。通过与海南测震台网地震编目及PTD法计算结果进行对比,发现几种方法测定的震源深度具有较好的一致性,表明利用sPL震相确定中小地震震源深度是可靠的。
本文结果初步证实海南岛能够观测到sPL震相。对于海南数字测震台网监测到空隙角大的小地震,可以利用sPL震相确定震源深度,有助于提高该台网震源参数产出的准确性。
感谢陕西省地震局赵韬工程师对论文撰写给予热心帮助和悉心指导。
| 包丰, 倪四道, 赵建和, 等. 时钟不准情形地震精确定位研究——以2011年1月19日安庆地震序列为例[J]. 地震学报, 2013, 35(2): 160-172. | |
| 崇加军, 倪四道, 曾祥方. sPL, 一个近距离确定震源深度的震相[J]. 地球物理学报, 2010, 53(11): 2620-2630. | |
| 龙锋, 阮祥, 宫悦, 等. 利用深度震相确定芦山地震主震及若干强余震的震源深度[J]. 地震研究, 2014, 37(3): 339-346. | |
| 任克新, 邹立晔, 刘瑞丰, 等. 用sPn计算内蒙地震的震源深度[J]. 地震地磁观测与研究, 2004, 25(3): 24-31. | |
| 魏娅玲, 蔡一川, 苏金蓉. 采用sPn震相确定甘肃岷县M > 4.0地震震源深度[J]. 地震工程学报, 2013, 35(3): 438-442. | |
| 项月文, 罗丽, 肖孟仁, 等. sPL震相在九江-瑞昌MS 5.7地震序列震源深度测定中的应用[J]. 华北地震科学, 2014, 32(2): 7-13. | |
| 詹小艳, 朱升初, 王恒知, 等. sPL震相在江苏高邮M 4.9级地震震源深度测定中的应用[J]. 地球物理学进展, 2014, 29(4): 1609-1614. DOI:10.6038/pg20140416 | |
| 朱元清, 石耀霖, 李平. 一种确定地震深度的新方法[J]. 地震地磁观测与研究, 1990, 11(2): 4-12. | |
| Aki K, Richards P G. Quantitative Seismology[M]. 2nd ed. Sausalito, CA: University Science Books, 2002. | |
| Bock G, Grünthal G, Wylegalla K. The 1985/86 western Bohemia earthquakes:modelling source parameters with synthetic seismograms[J]. Tectonophysics, 1996, 261(1/3): 139-146. | |
| Langston C A. Depth of faulting during the 1968 Meckering, Australia, Earthquake sequence determined from waveform analysis of local seismograms[J]. Journal of Geophysical Research, 1987, 921(B11): 11561-11574. | |
| Saikia C K. A method for path calibration using regional and teleseismic broadband seismograms:application to the 21 May 1997 Jabalpur, India earthquake (MW 5.8)[J]. Current Science, 2000, 79(9): 1301-1315. |
 2017, Vol. 38
2017, Vol. 38

 ,
,